Динамические измерения. Проблемы динамических измерений. Входные сигналы и измеряемые величины. Погрешности динамических измерений, страница 16

                                                                                                         (14)

Где  - оператор, характеризующий отличие преобразования непрерывных сигналов от масштабного.

 - функционал характеризующий отличие преобразования результирующего непрерывного сигнала в постоянный, осуществляющегося в СИ, от требуемого. Оценить на основе (14) можно лишь для конкретных функционалов  и Ф и оператора С, а также определенных сведений о входном сигнале устройства x(t).

Динамические погрешности измерительного преобразования.

Измерительное преобразование – наиболее типично заданное динамическое измерение. Преобразования условно разделяются по виду на пропорциональные и функциональные, т.е. с функцией отличной от линейной. В практике чаще сего имеют дело с пропорциональным преобразованием. Примеры: первичное преобразование сигнала неэлектрической величины в электрический сигнал, деление сигналов механических величин, ослабление уровня и мощности электрических сигналов.

Коэффициент пропорциональности преобразования может быть размерным как в случае первичного преобразования, и безразмерным в остальных примерах. В последнем случае преобразование называется масштабным.

Рассмотрим оценивание погрешностей измерений по формуле (8)

                                                   (8)

где

В предположении, что устройство описывается дифференциальным уравнением. Выражение (8) показывает, что  зависит как от динамических свойств СИ, так и от спектральных свойств измеряемой величины. В связи со сложностью задачи ее решают по этапах.

Оценивание погрешностей начинается на этапе подготовки измерений, при выборе СИ. Априорное оценивание погрешностей при выборе СИ осуществляют с использованием информации о возможных входных сигналах и сведений о динамических свойствах имеющихся устройств. Его производят также с целью изучения возможностей СИ данного типа при его использовании для измерений. В последнем случае оценивают ожидаемые погрешности при воздействии на устройство сигналов типовых форм.

Если ДИ входит в состав ответственных исследований или возникает сомнение в том, что реальный выходной сигнал и условия измерений соответствовали предполагаемым, может вызвать необходимость уточнить априорную оценку по результатам измерений. Формально, такое апостериорное оценивание есть есть нахождение оценки  по выражению (8).

Когда не удается выбрать достаточно быстродействующее СИ либо когда необходимо осуществить предельно точные измерения, требуется скоректировать погрешность измерений. Коррекция статической погрешности осуществляется путем индивидуальной градуировки средства измерения. В предположении пренебрежимо малой статической погрешности коррекция динамической погрешности формально сводиться к решению обратной задачи динамики – нахождению x(f). Эта задача относиться к некорректно поставленным и представляют наибольшую сложность при обработке данных измерений.

Поскольку погрешность измерений обусловлена свойствами как СИ, так и входного сигнала, то формулировка конкретной задачи её оценивания определяется характером и объемом сведений об этих свойствах, а сложность решения – дефицитом имеющийся информации, Выявление наиболее распространенных вариантов исходной информации позволяет сформулировать типичные задачи оценивания. Рассмотрим некоторые из этих задач

1.  Точное априорное оценивание

Пусть имеется СИ с дифференциальным уравнением

                                                                                 (15)

При непрерывных на интервале [0,t] входных воздействий x(t) решение уравнений можно представить в виде:

                                                                         (16)

Где y₂ (t) – частное решение уравнения (15)

f₁ и f₂ –линейно независимые решения соответствующего однородного уравнения.

С₁ и С₂ – константы, определяемые начальными данными.

Эти начальные данные не могут задаваться произвольно, т.к. решение не должно быть непрерывно в точках разрыва функции x(t)

Начальное условие  должно удовлетворять условию

   

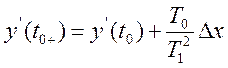
Введем обозначение

; 

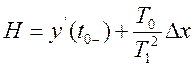
Тогда в зависимости от значений коэффициента Т₁ и Т₂ (уравнение (15)) можно выделить 3 группы соотношений для Ф₁ и Ф₂, С₁ и С₂ в решении (16)

1. ; ; 

Где  - корни квадратного уравнения

2. ;  ; 

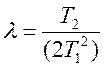
3.                                     

                                                                 

              

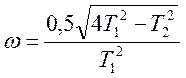
Эти соотношения позволяют определить отключение устройства на входных сигналах в случае, когда удается найти частное решение.

2.  Приближенное априорное решение оценивания

Для получения приближенного априорного значения измерения мы также априорно информируем о характере изменения во время измерения величины входящих сигналов. Наибольший общий результат, полученный для устройства с монотонной переходной характеристикой. Для таких приборов при сигнале с нулевым начальным значением справедливо:

 

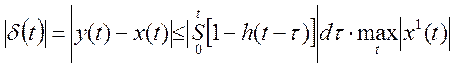
                                                                                                         (20)

где М – const, характеризующая модуль интеграла в правой части.

Для WT уравнения 1-го порядка М=Т, для WT уравнения 2-го порядка переходная характеристика может иметь немонотонный характер. Остановимся на случае:При уравнение (21) описывает динамику устройства, составленное из двух последних звеньев 1-го порядка. Погрешность такого уравнения не превысит оценок сверху для каждого из этих звеньев.

                                                                                                           (21)

Аналогичные рассуждения позволяют получить оценку погрешности для средств измерения состоящих из  произвольного числа последовательно соединенных звеньев 1-го порядка.

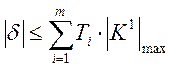                                                                                                             (23)

При вместо (22) получаем:

                                                                                                    (24)

(23), (24) могут быть использованы при любом сигнале с изв скоростью изменения и нулевым начальным значением.

Остановимся на случае: