Динамические измерения. Проблемы динамических измерений. Входные сигналы и измеряемые величины. Погрешности динамических измерений, страница 13

При цифровой обработке определяющим является метод использующий сигнал и погрешность интегрирования. С ростом частоты повторения тактовых импульсов, определяется масштаб величин при частном анализе псевдослучайных сигналов отличие корелляционных и спектральных свойств этой двоичной М-последовательности от аналогичных свойств белого шума.

Оценивание погрешности динамических измерений.

Составляющие погрешности динамических измерений.

Погрешность динамических измерений в соответствии с общим определением погрешности ГОСТ 16.263-70 имеет собой разность:

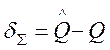,                                                                                                    (1)

Где  - результат измерения,

Q – измеряемая величина.

При измерении в динамическом режиме постоянной физической величины Q эта погрешность  является постоянной величиной детерминированного или случайной. При измерении измеряемых величин Q(t)  является детерминированной или случайной функцией времени. При оценивании погрешности динамических измерений в соответствии с (1) сохраняется этот же общий подход, выработанный в процессе статических измерений. Он состоит в анализе погрешности измерения, расчленении ее на составляющие, теоретическое и экспериментальное исследование, оценивание, синтез общей погрешности в частности путем суммирования оценок составляющих.

Изучаемое свойство объекта исследования выражено истинным значением сигнала x_n(t). Измеряемая величина в общем случае определяется как результат функции преобразования сигнала x_n (t)

                                                                                                     (2)

В_н – требуемый, т.е. номинальный оператор преобразования

Ф_н – требуемый, т.е. номинальный функционал

Вследствие взаимодействия средства измерения с объектом действительного сигнала объекта (номинальное значение x_n(t)) будет отличаться от x_и(t). На вход измерительного устройства кроме x_н(t) действует ошибка (t). Следовательно действительный сигнал отличается от x_н(t). С помощью средства измерения осуществляется преобразование  входного сигнала в выходной. Операция преобразования В₀ отличается от В_н в силу следующих причин. Действительно операция В_0Т выражающая преобразование данного типа, отличается от В_н из-за несовершенства принципа действия и конкретного устройства. Индивидуальные свойства конкретных экземпляров СИТ выражаются с помощью оператора В_ДЭ, отличны от типовых. Кроме того, в процессе преобразования на устройство воздействуют влияющие величины  (в общем случае изменяющееся), совокупное действие которых может быть выражено влияющим сигналом , обуславливающим возмущение оператора В_ДЭ. В результате отсчитывания  значений y_Д(t) с погрешностью образуется сигнал . Вычисление действительного функционала Ф_Д(t) может либо входить составной частью в алгоритм работы СИ, либо производиться путем обработки значений выходного сигнала устройства, отсчитываемых по его шкале. В последнем случае следует учитывать по отдельности погрешность отсчитывания и погрешность вычислений. За результат измерения принимается величина:

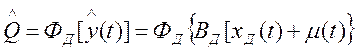                                                                           (3)

Погрешность равна

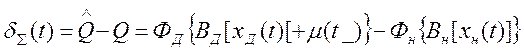                                                   (4)

Преобразуем выражение (4) в предположении линейности операторов и функционалов следующих образцов в соответствии с представленной схемой:

 (5)

Соотношение (5) позволяет проаппроксимировать составляющие погрешностей. Характер Составляющих и их взаимосвязь в значительной мере обусловлены сигналом. Характер этого сигнала определяется задачей исследования и свойствами помехи. В отношении этих факторов можно выделить 2 основных варианта. Если исследуются закономерные изменения состояний объекта, то сигнал х_и будет детерминированным. Поскольку воздействие СИ с объектом являются регулярными, в этом случае х_н также будет детерминированным. Если к тому же случайная помеха пренебрежимо мала, то будет детерминированным и сигнал х_Д.

В том случае, когда исследуется объект со случайными характеристиками и (или) случайная помеха существенна, сигнал х_Д оказывается случайным. Погрешность, обусловленная взаимодействием СИ с объектом, может быть представлена с помощью разности:

В зависимости от указанных выше вариантов задачи исследования сигналы х_Н, х_И и соответственно погрешность  могут оказаться либо детерминированными, либо случайными функциями времени. Помеха  рассматривается обычно как аддитивная величина по отношению к сигналу х_н, содержащая в общем случае детерминированную и случайную части, т.е. может быть выражена случайной функцией времени с ненулевым мат ожиданием.

. Соответствующая составляющая погрешности .

Отклонение  оператора СИ данного типа В_ДТ от В_Н носит регулярный характер, поэтому характер составляющей погрешности преобразования, обусловленной указанной погрешностью.

Определяется сигналом х_Д. Т.о. погрешность  может быть и детерминированной и случайной функцией времени.

Отклонение оператора В_ДЭ конкретного экземпляра СИ от В_ДТ рассматривается как случайное по множеству устройств данного типа, поэтому все зависит от х_Д соответствующая составляющая погрешности.

Представляет собой случайную функцию времени. Погрешность вызванная вариацией оператора В_ДЭ под воздействием влияющего сигнала, сложным образом зависит от него. Эта зависимость детерминирована, однако вследствие того что содержит детерминированную и случайную составляющие, вариация и обусловленная ею погрешность будут иметь такие же  составляющие. Таким образом из-за вариации погрешность равна

Где В_Д – возмущенный оператор СИ. Величина  - случайная с ненулевым мат ожиданием. Е=n. Погрешность отсчитывания является аддитивной по отношению к сигналу y_Д(t) и содержит в общем случае систематическую  и случайную составляющую. Т.о.

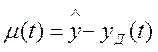есть случайная функция с ненулевым мат ожиданием Е. Соответствующая составляющая погрешности равна 

Погрешность вычислений определяется отклонением действительного функционала Ф_Д от Ф_Н.