Раздел. Практические занятия.
Модели объектов регулирования.
1. Модель одноемкостного объекта регулирования.
2. Модель двухемкостного объекта регулирования с запаздыванием.
2.1. Методика расчета величин T1 и T2 по разгонной характеристике объекта, снятой экспериментально.
3. Модель измерительного устройства расхода жидкости (объект регулирования).
4. Модель измерительного устройства расхода газа (объект регулирования).
5. Регулирование процесса смешения.
5.1. Модель объекта регулирования.
5.2. Система регулирования концентрации продукта на выходе смесителя.
6. Модель теплообменника смешивающего типа.
7. Модель ресивера.
8. Теоретическая модель резервуара.
Модели элементов систем автоматического регулирования.
9. Регуляторы (их применение, модели).
9.1. Схема системы автоматического регулирования.
9.1.1. Определения.
9.1.2. Качественные показатели систем автоматического управления промышленными объектами.
9.2. Области применения регуляторов разных типов.
9.2.1. Пропорционально регуляторы (рекомендации по их применению).
9.2.2. Интегральные регуляторы (рекомендации по их применению).
9.2.3. Пропорционально-дифференциальные регуляторы (рекомендации по их применению).
9.2.4. Пропорционально-интегральные регуляторы (рекомендации по их применению).
9.2.5. Пропорционально-интегрально-дифференциальные регуляторы (рекомендации по их применению).
10. Гидравлический исполнительный механизм.
11. Модель датчика давления.
11.1. Математическая модель сильфонного и мембранного датчиков давления.
11.1.1. Измерение давления в жидкости.
11.1.2. Измерение давления газов.
12. Математическая модель чувствительного элемента уровня поплавкового типа.
12.1. Математическая модель чувствительного элемента уровня поплавкового типа с пружиной.
12.2. Математическая модель чувствительного элемента уровня поплавкового типа без пружины.
13. Модель пневматического мембранного исполнительного механизма (МИМ) с противодействующей пружиной и пневмопроводом.
13.1. Пневматический мембранный исполнительный механизм (МИМ) с противодействующей пружиной.
13.2. Пневмопровод.
13.3. Упрощенная модель пневматического исполнительного механизма с пневмопроводом:
13.4. Полная модель «пневмопровод + МИМ».
14. Передаточная функция электропривода крана.
14.1. Передаточная функция согласующего устройства.
14.2. Передаточная функция электродвигателя.
14.3. Передаточная функция редуктора.
14.4. Передаточная функция механизма привода штока крана.
14.5. Передаточная функция электропривода в целом.
Модели объектов регулирования.
Рассматриваются четыре типовых объекта, которые могут являться объектами регулирования в различных технологических цепочках химического производства: (а) - термостат; (б) - емкость для жидкости, приток которой и отток происходят самотеком; (в) - емкость для жидкости, приток которой происходит под давлением, а отток самотеком; (г) - ресивер.
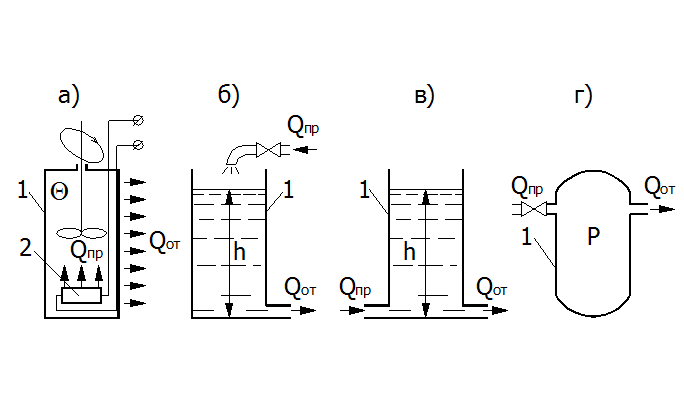
Рис. 1. Одноемкостные объекты регулирования.
Составление модели объекта.
Модель объекта будем составлять именно как модель объекта регулирования. При этом в качестве регулируемого (выходного) параметра в первом случае будет рассматриваться температура жидкости в емкости θ, во втором и третьем - уровень жидкости в баке h, в четвертом – давление в ресивере P.
Составление модели объекта рассмотрим на примере а).
Запишем уравнение баланса.
![]()
В случае нарушения баланса часть энергии соберется в емкости. Уравнение баланса в этом случае примет вид
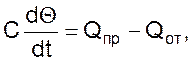 (01)
(01)
где Qпр – приток тепла, ккал/с или квт;
Qот – отток тепла, ккал/с или квт;
Θ - температура, ˚С;
С – теплоемкость среды в объекте, ккал/град или кДж/град (С = c•m, где c и m – удельная теплоемкость и масса объекта соответственно).
Принимая, что отток тепла (теплопотери) Qот зависит от температуры Qот = f(θ) и, полагая эту зависимость линейной, получим так называемое уравнение самовыравнивания объекта
![]() (02)
(02)
где ρ – коэффициент самовыравнивания, ккал/(с•град) или квт/град.
Смысл названия «коэффициент самовыравнивания» состоит в том, что в случае если этот коэффициент больше нуля, то объект сам без внешнего воздействия всегда приходит к некоторому установившемуся состоянию, причем, тем быстрее и тем с меньшим статическим отклонением, чем больше этот коэффициент.
Подставляя 02 в 01, получим дифференциальное уравнение, описывающее поведение объекта
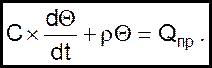 (03)
(03)
Преобразуем полученное уравнение к виду, принятому для записи. Разделим обе части уравнения на коэффициент самовыравнивания ρ.
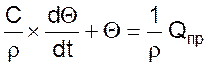 (04)
(04)
Обозначив, C/ρ через T0, 1/ρ через k получим выражение
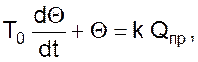 (05)
(05)
где T0 – постоянная времени объекта, с;
Qпр – приток тепла, ккал/с или квт;
k – коэффициент усиления (передачи) объекта, град/квт, (с•град) /ккал.
Или, принимая обобщенные обозначения θ = у и Qпр = х, запишем
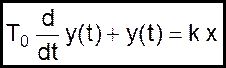 (06)
(06)
Нахождение дифференциального уравнения реального объекта.
Для нахождения дифференциального уравнения реального объекта необходимо знать величины Tо (или С), ρ (или k) и x(t).
Постоянную времени технологического объекта Tо можно принимать как отношение объема аппарата (V, м3) к расходу рабочей среды через аппарат (Q, м³/с)
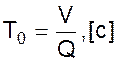
Степень (коэффициент) самовыравнивания определяют двумя путями: из анализа физических характеристик процесса или на основании опытных данных. В последнем случае степень самовыравнивания определяют по величине коэффициента передачи объекта:
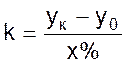 ,
, 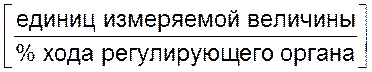
где yк – конечное значение, которое приобретает значение измеряемой величины при возмущающем воздействии x.
Передаточная функция одноемкостного объекта примет вид:
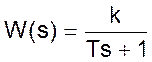 (07)
(07)
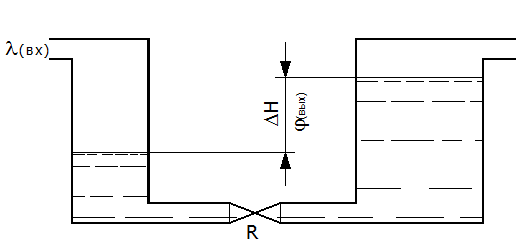
φ – относительная величина регулируемого параметра;
λ – относительная величина возмущающего воздействия;
R – местное сопротивление.
Примерами двухъемкостных объектов с запаздыванием могут служить теплообменник поверхностного типа, варочный котел непрямого подогрева и ректификационная колонна. Для них характерным является незначительное местное сопротивление. А это означает, что все они могут удовлетворительно аппроксимироваться апериодическим звеном второго порядка с запаздыванием, которое может быть описано дифференциальным уравнением второй степени с постоянными коэффициентами.
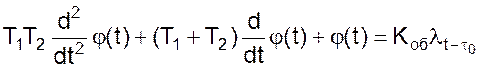 (01)
(01)
где φ - Относительное изменение регулируемого параметра y;
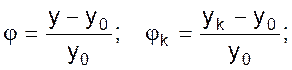
где φk - конечное значение регулируемого параметра при t → ∞ и при отсутствии регулирующего воздействия;
λ – относительная величина возмущающего воздействия x.
В операторной форме это уравнение примет вид:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.