Модели объектов регулирования. Модели элементов систем автоматического регулирования, страница 5

Рассмотрим статическую характеристику объекта. Из самых общих соображений зависимости Q_пр и Q_от, от уровня жидкости в резервуаре Н, можно представить в виде, изображенном на рис. 2.

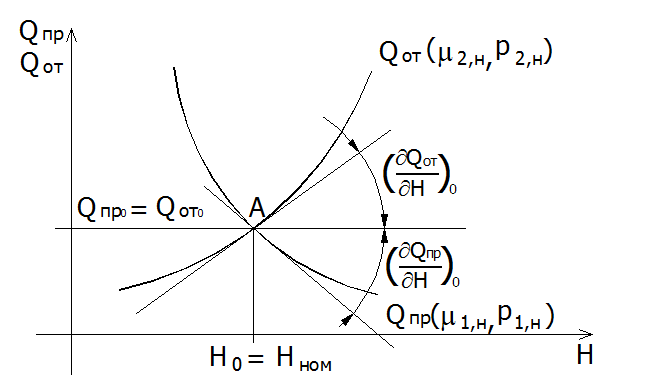
Рис.2. Статические характеристики резервуара.

Принимая давления на входе в резервуар р_1н и выходе из него р_2н постоянными, можно считать, что приход жидкости в резервуар и отток из него являются функциями коэффициентов истечения кранов и уровня жидкости в резервуаре.

,                                                (02)

Запишем уравнение баланса для динамической модели. При ее составлении примем, что разность притока и оттока жидкости аккумулируется в емкости.

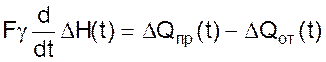                                                        (03)

где   F – площадь поперечного сечения резервуара, м²;

         ∆Q_пр – приток жидкости в резервуар, кг/с;

         ∆Q_пр – отток жидкости из резервуара, кг/с;

         ∆Н – приращение высоты столба жидкости в резервуаре, м.

На основании 02 для приращений притока и оттока, линеаризуя их в точке равновесия, можно записать

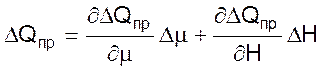                                                         (04)

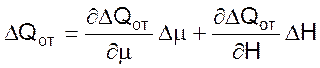                                                         (05)

Перепишем уравнение 03 в соответствии с последними выражениями

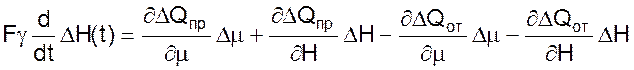            (06)

Разрешим уравнение относительно ∆Н

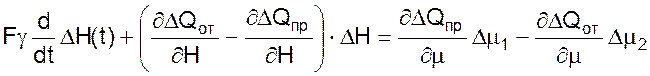                    (07)

Введем безразмерные относительные отклонения относительно номинальных значений параметров

,     ,

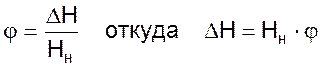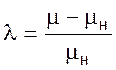а члены левой части уравнения разделим на Q_н

Учитывая последнее, запишем

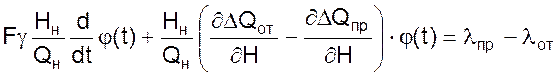                       (08)

Или

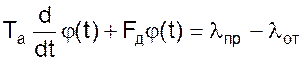                                                           (09)

где 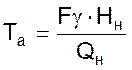  , с – время разгона объекта;

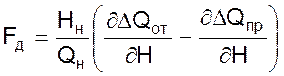          - коэффициент самовыравнивания объекта.

Для составления аналитической модели, мы должны решить две задачи: определить численное значение время разгона объекта Т_а и определить численные значения коэффициентов самовыравнивания на линиях притока λ_пр и оттока жидкости λ_от для нашего объекта.

Определим время разгона объекта.

Решение задачи начнем с того, что определим высоту столба жидкости над дном резервуара H₀.

Запишем уравнение баланса

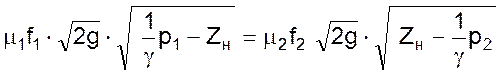
где     Z_н – номинальный уровень жидкости в рассматриваемой гидравлической системе;

          g – ускорение свободного падения.

Найдем численные значения коэффициентов данного уравнения для установившегося режима работы.

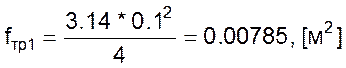
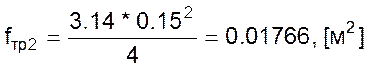
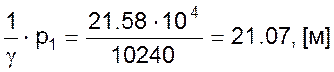
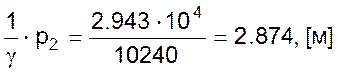
С учетом вычисленных значений коэффициентов балансовое уравнение примет вид

Разрешив последнее уравнение относительно Z_н, получим

Z_н = 8.474 м.

При этом расход жидкости Q₀, будет равен

 

Высота столба жидкости над дном резервуара H₀  будет равна разности между вычисленным значением уровня Z_н и высотой столба жидкости Z_P2,н, эквивалентного давлению подпора р_2,н на линии.

 

 

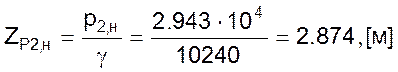
Площадь поперечного сечения резервуара равна

       

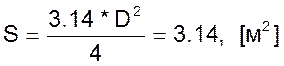
Тогда аккумулированный в резервуаре объем жидкости будет равен

    

Время разгона для объекта будет равно

              

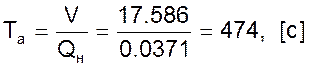
Определим  коэффициенты самовыравнивания на стороне прихода жидкости и ее оттока.

Перепишем уравнения прихода и оттока жидкости, выразив значение уровня жидкости в гидравлической системе  в установившемся состоянии Z₀ через высоту столба жидкости над дном резервуара H  (Z₀ = H₀ +2.847),

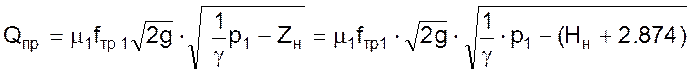
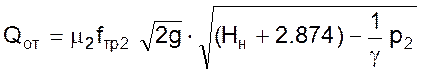
Тогда, подставив значения f_тр1, f_тр2, μ₁, μ₂, γ, и  g в формулы получим

Откуда найдем значения коэффициентов самовыравнивания на стороне прихода и оттока жидкости.

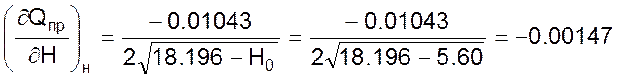
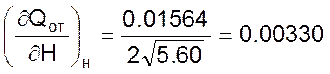
Из полученного определим коэффициент самовыравнивания объекта, который  будет равен

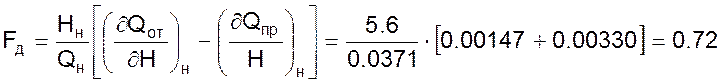
Дифференциальное уравнение, описывающее объект, будет иметь вид

где     λ – относительное управление (в долях номинальных значений управляющих сигналов) 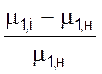,  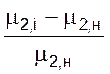(μ_1,н = 0.3, μ_2,н = 0.2);

         φ – относительное отклонение .

Решение дифференциального уравнения будет иметь вид

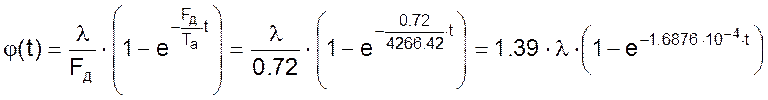
Уровень жидкости в резервуаре будет равен

С учетом вычисленных значений дифференциальное уравнение примет вид

            ПОВТОР!!!   (Изменена форма записи)

Приведем уравнение к канонической форме записи для чего разделим обе части уравнения на F_д.

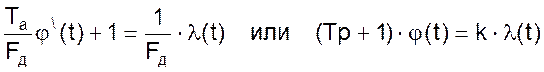
Вычислим постоянную времени объекта

       

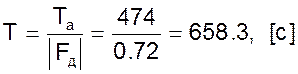
и коэффициент усиления

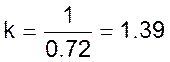
Тогда можно записать для объекта

           

С учетом полученного, передаточная функция объекта будет иметь вид

                           

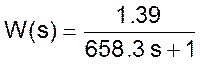
Задание для исследования модели.

Исследовать переходной процесс:

■  при номинальных значениях коэффициентов истечения: μ_1,ном = 0.3; μ_2,ном = 0.2:

■  при изменении коэффициента истечения крана на приходе с  номинального значения μ_1,ном = 0.3  до μ_1,i = 0.2 (при этом коэффициент истечения крана на выходе μ₂ остается номинальным);

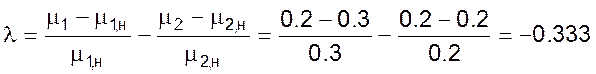
■  при изменении коэффициента истечения крана на оттоке с номинального значения μ_2,ном = 0.2  до  μ_2,i = 0.3 (при этом коэффициент истечения крана на входе μ₁ остается номинальным);

 

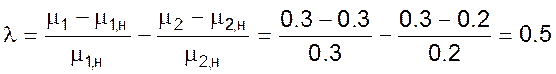
■  при изменении коэффициента истечения крана на приходе с  μ_1,н = 0.3 до μ₁ = 0.2 и изменении коэффициента истечения крана на оттоке с  μ_2,н = 0.2 до μ₂ = 0.3.

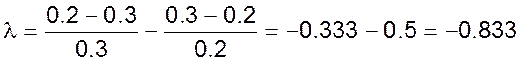
■  при изменении коэффициента истечения крана на приходе с  μ_1,н = 0.3 до μ₁ = 0.5 и изменении коэффициента истечения крана на оттоке с  μ_2,н = 0.2 до μ₂ = 0.2.

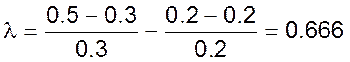
Модели элементов систем автоматического регулирования.

9 .  Регуляторы (их применение, модели).

9.1.1.    Схема системы автоматического регулирования.

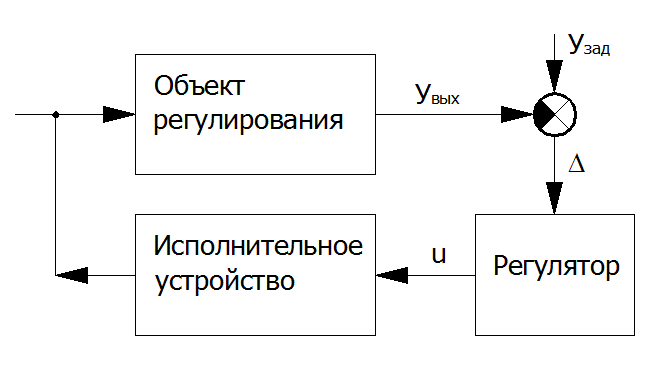
Рис. 3. Схема системы автоматического регулирования.

9.1.1.1.    Определения.

Область параметров настроек реальных регуляторов, совпадающая достаточно хорошо с областью настроек идеальных регуляторов называется областью нормальных режимов регуляторов. Работа регулятора в этой области обеспечивается определенной совокупностью значений амплитуд и частот входных сигналов и параметров настройки регулятора. Как правило, область нормальных режимов регулятора определяется при его разработке.