Модели объектов регулирования. Модели элементов систем автоматического регулирования, страница 6

Мы при создании модели регулятора априори будем считать, что он работает в области нормальных режимов.   

Наибольшее распространение получили регуляторы следующих типов:

■  P – пропорциональные;

■  I – интегральные регуляторы;

■  PD – пропорционально-дифференциальные;

■  PI – пропорционально-интегральные;

■  PID – пропорционально-интегрально-дифференциальные.

Передаточная функция PID регулятора имеет вид

 

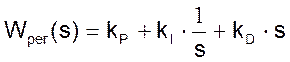
Блок дифференцирования регулятора носит название «блок предварения».

PI регуляторы характеризуются параметром, который называется «время изодрома» (время удвоения входного сигнала).

При нулевых начальных условиях и действии на вход PI регулятора единичной функции  выходной сигнал регулятора с течением времени будет изменяться по закону

Время, в течение которого выходной сигнал u(t) станет равным 2k_P, и будет называться «временем изодрома» Т_I.

.

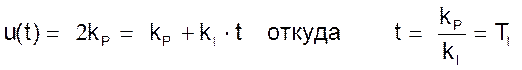Из чертежа следует

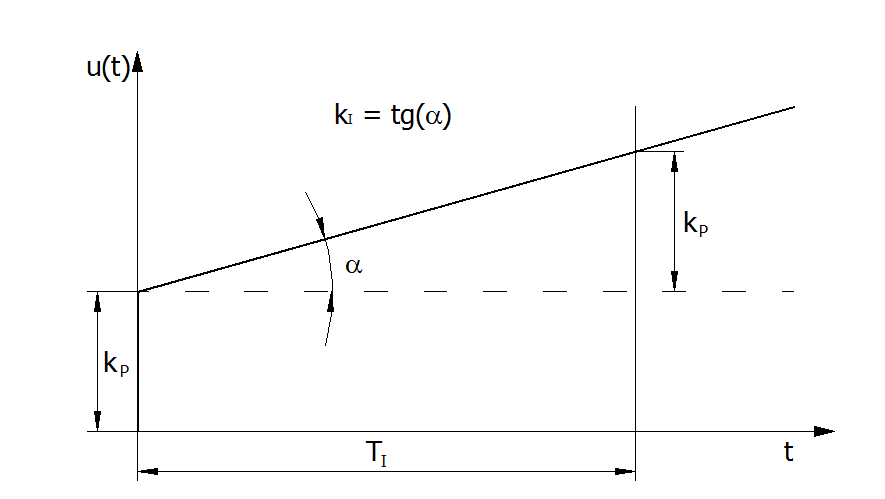
Рис.1 Определение времени изодрома.

PID регулятор характеризуется помимо параметра «время изодрома» еще одним параметром «время предварения».

Время предварения равно

.

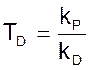Модель регулятора в соответствии с его уравнением можно представить в виде:

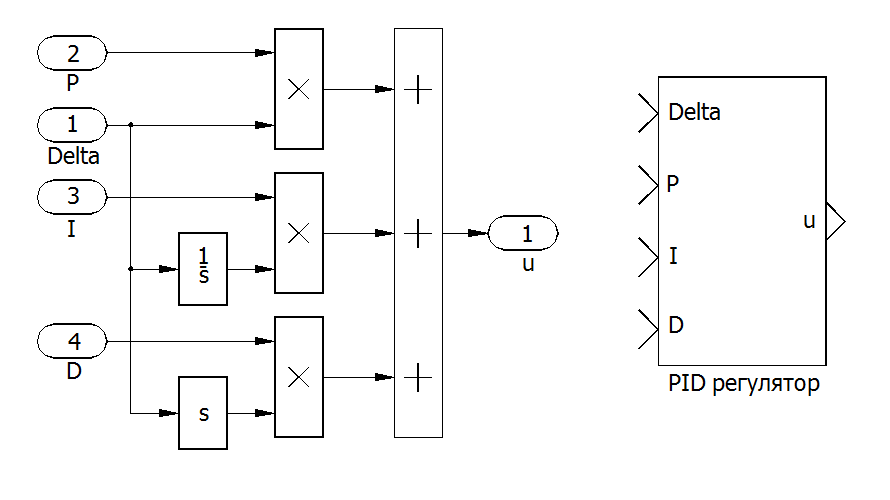
Рис. 2. Модель PID регулятора в пиктограммах SIMULINK.

9.1.1.2.   Качественные показатели систем автоматического управления промышленными объектами[1].

К основным качественным показателям систем автоматического управления промышленными объектами можно отнести:

1)   время регулирования - время, в течение которого отрабатывается скачкообразное изменение управляющего или возмущающего воздействия;

2)   перерегулирование – наибольшее отклонение регулируемого параметра от установившегося значения при внезапном изменении задания или под действием возмущающих сил;

3)   динамический коэффициент регулирования – отношение максимального отклонения регулируемого параметра от величины заданного значения в переходном процессе, вызванное скачкообразным возмущением, к отклонению от задания при таком же возмущении, но без регулятора;

4)   запас устойчивости – зависимость между изменениями каких либо параметров системы или характеристика, определяющая удаление годографа передаточной функции разомкнутой системы от критической точки;

5)   степень устойчивости – абсолютное значение вещественной части корня характеристического уравнения, ближайшего к мнимой оси;

6)   колебательность системы – тангенс половины угла, внутри и на границах которого расположены все корни характеристического уравнения;

7)   максимальное ускорение, с которым изменяется регулируемая величина при заданном ступенчатом управляющем воздействии;

8)   установившаяся погрешность регулирования – величина, характеризующая точность отработки задания регулирования в переходных и установившихся режимах;

9)   интеграл  квадрата отклонения регулируемой величины от ее заданного значения или интеграл квадрата отклонения регулируемой величины от заданного значения плюс сумма некоторого числа производных этого отклонения в квадрате;

10)  среднеквадратическое значение отклонения регулируемой величины от заданного значения при случайном характере возмущений;

11)  наименьшая возможная длительность отработки начального отклонения (оптимальность по быстродействию);

12)  наименьшее возможное перерегулирование (оптимальность по перерегулированию);

13)  среднеквадратическое значение отклонения регулируемой величины от заданного значения плюс интеграл от квадрата отклонения или показатели, характеризующие процессы при отработке начального отклонения;

14)  максимально допустимые значения амплитуды и частоты автоколебаний регулируемого параметра.

Для систем взаимосвязанного регулирования имеются дополнительные показатели: автономность или инвариантность одних регулируемых параметров к возмущениям, действующим в контурах регулирования других параметров.

При каскадном включении регуляторов когда один регулятор (ведущий) «ведет» другие (ведомые) показателем может быть определенное соотношение скоростей протекания переходных процессов и заданная точность.

Даже далеко не полный перечень качественных характеристик автоматического регулирования показывает, что удовлетворить всем требованиям да еще одновременно просто невозможно, более того некоторые из них являются взаимно противоречивыми. Естественно предложить выбрать несколько из них в качестве основных, а остальные считать второстепенными и не предъявлять к ним особых требований. При таком разделении следует руководствоваться требованиями технологического процесса.

9.1.2.    Области применения регуляторов разных типов.

9.1.2.1.   Пропорционально регуляторы (рекомендации по их применению)[2].

Применение пропорциональных регуляторов определяется допустимым значением установившейся погрешности и устойчивостью. Другими словами, возможное наибольшее значение коэффициента усиления пропорционального регулятора должно быть таковым, что с одной стороны обеспечивается допустимое значение установившейся погрешности, а с другой, - устойчивость регулируемой системы в целом[3].

Пропорциональный регулятор, включенный последовательно с астатическим исполнительным устройством типа

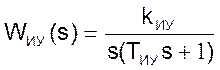
относится к интегральным регуляторам.

9.1.2.2.   Интегральные регуляторы (рекомендации по их применению).

Интегральные регуляторы не могут обеспечить устойчивости нейтральных объектов и объектов с отрицательным самовыравниванием без запаздывания и с запаздыванием, так как такие объекты структурно не устойчивы[4].

9.1.2.3.   Пропорционально-дифференциальные регуляторы (рекомендации по их применению).

Применение PD регуляторов дает возможность увеличивать общее усиление при сохранении устойчивости системы, что резко улучшает качество переходных процессов.