где kВ.ТР – для масла при температуре 1000С, Па3с;
DC – диаметр сильфона = 0.03, м.
Тогда можно будет записать
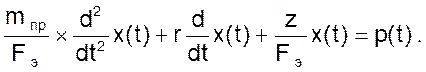 (06)
(06)
Передаточная функция на основании последнего уравнения примет вид
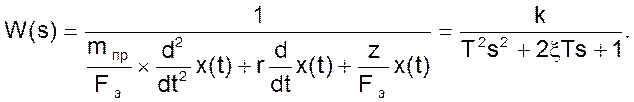 (07)
(07)
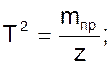
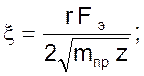
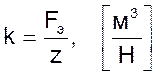
При уменьшении диаметра трубок коэффициент ξ вследствие увеличения коэффициента r растет значительно быстрее, чем постоянная времени T. В связи с этим, уравнение 03 может быть записано в виде
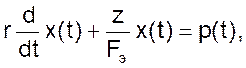 (08)
(08)
Соответственно передаточная функция в этом случае приобретет вид
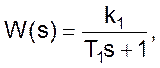 (09)
(09)
где 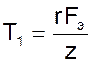 и
и 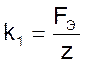
При измерении давления газа уравнение динамики чувствительного элемента будет выводиться иначе.
В этом случае в уравнении движения элемента массой газа можно пренебречь
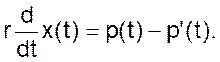 (10)
(10)
где 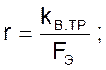
kВ.ТР. – коэффициент вязкого трения. Для воздуха kВ.ТР = 181310-7 [МПа.с]. (Краткий справочник по химии. Гороновский И.Т. и др., Наукова думка, 1974, [712]);
FЭ – эффективная площадь дна сильфона.
Однако массой подвижных частей чувствительного элемента пренебрегать нельзя.
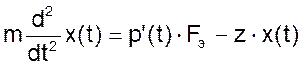 (11)
(11)
где z – упругость пружины, Н/м;
m - приведенная масса подвижных частей чувствительного элемента, кг.
Решая оба уравнения совместно можно написать
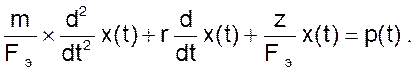 (12)
(12)
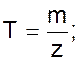
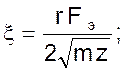
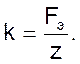
Как видим, уравнения отличаются друг от друга только значениями инертных масс.
Однако ввиду малой инерционности самих пневматических систем собственную частоту чувствительных элементов следует учитывать. Считается, что с помощью мембранного измерителя можно с допустимой погрешностью измерять нестационарное давление, в котором частота наивысшей гармоники, имеющей существенное значение, будет меньше 0.3 частоты собственных колебаний мембраны.
Схема чувствительного элемента датчика уровня поплавкового типа с пружиной представлена на рисунке 1.
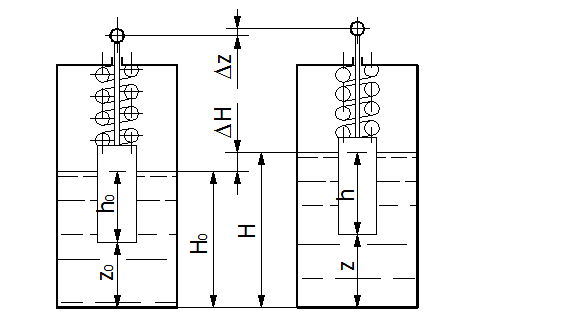
Рис. 1. Схема чувствительного элемента уровня поплавкового типа с пружиной.
Математическую модель чувствительного элемента поплавкового типа с пружиной, представленного на рис. 1.
Составим уравнение баланса сил, действующих на поплавок чувствительного элемента в установившемся состоянии.
![]() (01)
(01)
где F↓ – восстанавливающая сила, Н;
F↑ - поддерживающая сила, Н.
Уравнение для восстанавливающей силы может быть записано в виде
![]() (02)
(02)
где F↓ – восстанавливающая сила, Н;
Gп – вес поплавка, Н;
F0 – начальное усилие пружины (настройка чувствительного элемента);
C – жесткость пружины;
Δz – деформация пружины.
В качестве исходных предпосылок будем считать: поплавок имеет постоянное сечение по высоте, уровень жидкости открытый.
Уравнение для поддерживающей (подъемной) силы поплавка F↑ будет иметь вид
![]() , (03)
, (03)
где γ – удельный вес жидкости, Н/м3;
S – площадь поперечного сечения поплавка, м2;
h – высота погруженной в жидкость части поплавка, м.
Уравнение статического равновесия 01 с учетом представленных зависимостей примет вид
![]() (04)
(04)
В нашем случае, как это следует из рис.1, подъемной силе поплавка противодействует вес поплавка и усилие пружины. Следует отметить: перемещение поплавка Δz будет меньше изменения уровня ΔН вследствие изменения заглубления поплавка h
Принимая
![]()
для поддерживающей силы можно записать
![]() , (05)
, (05)
а уравнение 4 представить в виде
![]() (06)
(06)
Теперь, имея в обеих частях уравнения члены, являющиеся функциями z, определим фактор устойчивости объекта Fд.
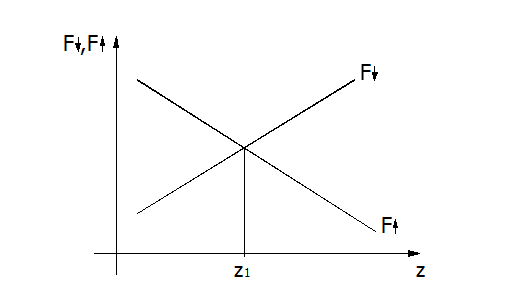
Рис. 3. Статическая характеристика восстанавливающей и поддерживающей сил чувствительного элемента уровня.
Фактор устойчивости Fд для данной системы будет равен.
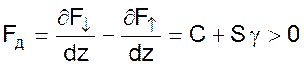 (07)
(07)
Он будет больше нуля, поскольку все величины, входящие в решение уравнения, физически не могут быть отрицательными.
Определим величину z для чего воспользуемся уравнением 06 откуда после несложных преобразований можно записать
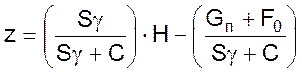 (08)
(08)
Составим уравнение динамики для чувствительного элемента.
Из уравнения 06 следует F↑(H, z) F↓(ψ, z), то есть F↑ зависит от высоты столба жидкости в резервуаре Н и сжатия пружины z, а F↓ зависит от настройки чувствительного элемента ψ и сжатия пружины z.
Запишем уравнение движения чувствительного элемента.
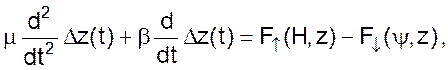 (09)
(09)
где μ – приведенная масса чувствительного элемента, кг;
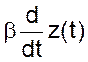 - сила гидравлического сопротивления
при движении поплавка (пропорциональна скорости перемещения);
- сила гидравлического сопротивления
при движении поплавка (пропорциональна скорости перемещения);
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.