Модели объектов регулирования. Модели элементов систем автоматического регулирования, страница 2

                                                                             (02)

Передаточная функция

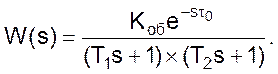                                                                                  (03)

Здесь               T₁ и T₂ – постоянные времени отдельных емкостей;

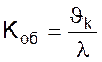           - коэффициент передачи объекта;

Для построения кривой разгона нужно решить дифференциальное уравнение (01) при этом, чтобы получить кривую разгона неколебательной формы необходимо соблюсти неравенство (T₁ + T₂)² > 4T₁T₂  при котором корни этого уравнения получаются действительными.

Решение уравнения в этом случае имеет вид

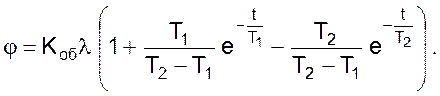                                                           (04)

Поскольку данные об объекте регулирования могут быть заданы в виде кривой разгона, познакомимся с процедурой определения величин постоянных объекта времени по разгонной характеристике.

2.1.  Методика расчета величин T₁ и T₂ по разгонной характеристике объекта, снятой экспериментально.

Величины T₁ и Т₂ мы будем рассматривать как  постоянные времени отдельных емкостей объекта.

Кривая разгона для двухъемкостного объекта имеет S – образный вид с точкой перегиба А.

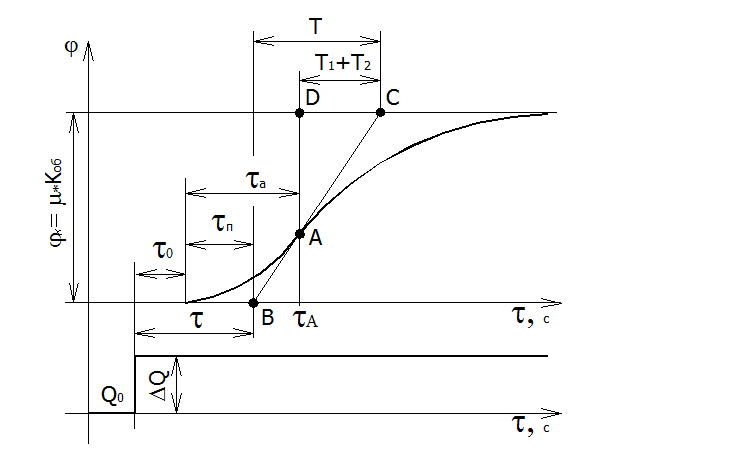
Будем рассматривать кривую как две отдельных: первую на промежутке времени от 0 до t_А и вторую - от t_А до бесконечности. Значение t_А определим, учитывая, что в этой точке скорость изменения параметра будет наибольшей.

Продифференцируем дважды уравнение (04). После чего, приравняв полученное уравнение нулю, и, решив его относительно t_А,  получим

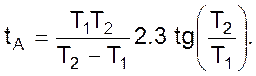
Проведем через точку перегиба касательную. Проекцию этой касательной на ось абсцисс ВС назовем условной постоянной времени объекта T (тем самым мы условно аппроксимируем данный объект апериодическим звеном).

Значение T можно найти из предположения, что она представляет собой время нахождения рабочей среды в аппарате и численно равна отношению объема аппарата (V, м³) к расходу рабочей среды, проходящей через аппарат (Q, м³/с).

  

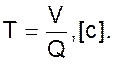
Вторая кривая представляет собой  экспоненту. Проекцию касательной на линию установившегося значения φ_k можно рассматривать как постоянную времени этой экспоненты и полагать, что она представляет собой сумму постоянных времени отдельных емкостей  T₁ + T₂.

Для того чтобы определить постоянные времени объектов мы поступим следующим образом: 

●  примем отношение (T₁ + T₂) / T  равным 0.76 – 0.8;

●  примем, что

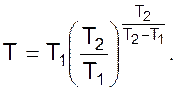
Переходное запаздывание t_п определяется величиной местного сопротивления R.

Общее запаздывание равно

3 .  Модель измерительного устройства расхода жидкости[1].

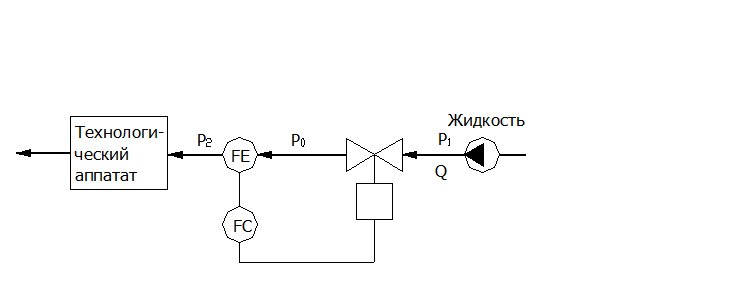
Рис. 1. Система регулирования расхода жидкости.

Р₁ – давление на входе, Па;

Р­­₀ – давление на участке после регулирующего крана, Па;

Р₂ – давление на участке за расходомерной диафрагмой, Па;

Q – расход рабочего тела, м³/с.

В качестве объекта регулирования рассматривается отрезок трубы между краном и сужающим устройством.  Расход рабочего тела через сужение определяется разностью давлений перед сужением и за ним. Разность давлений измеряется дифференциальным манометром, на выходе которого измерительный преобразователь формирует сигнал, пропорциональный расходу рабочего тела в сужении.

Сужающее устройство, дифференциальный манометр и измерительный преобразователь разности давлений можно рассматривать  безинерционные объекты.

Объект регулирования описывается дифференциальным уравнением первого порядка

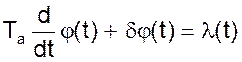
где   - время разгона объекта, с;

          - степень самовыравнивания объекта;

          - относительная величина возмущающего воздействия;

          - Относительная величина регулируемого параметра, ,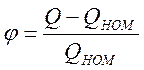

где   Q- текущее значение регулируемого параметра;

         Q_НОМ ­- номинальное значение регулируемого параметра.  

Время разгона объекта.

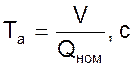
где    - объем трубопровода между краном и дроссельным устройством, м³;

         - номинальный расход жидкости, м³/с.

Степень самовыравнивания объекта.

,

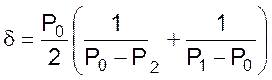где    - давление среды соответственно: на входе, на участке после регулирующего крана и на участке за расходомерной диафрагмой,  кПа.

Выбираем значение Р₀, принимая его равным заданному значению Р_ЗАД.

Перепад давления в расходомерной диафрагме.

,

где   - стандартный перепад давления в диффманометре-расходомере, Па;

         - модуль диафрагмы, равный 0.2 – 0.5.

Тогда

Перепад давления в регулирующем клапане.

.

Откуда давление Р₁ можно принимать равным

 

Максимально допустимое динамическое отклонение регулируемого параметра в переходном процессе.

.

Транспортное запаздывание объекта.

.

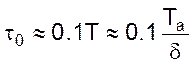Для очень малых значений объема трубопровода V  между краном и дроссельным устройством по сравнению с номинальным расходом Q_ном постоянная времени объекта T_а = 0; тогда

         

Перейдем к передаточной функции для чего запишем дифференциальное уравнение в нормальной форме

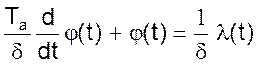
или

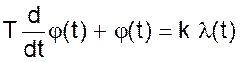
или

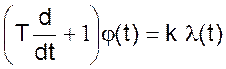
или

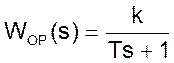
где   W_ОР – передаточная функция объекта регулирования.

Таким образом, передаточная функция измерителя расхода жидкости может быть представлена в виде:

 

где   W_ИР – передаточная функция измерителя расхода;

         W_СУ - передаточная функция сужающего устройства;

         W_ДМ - передаточная функция дифференциального манометра;

W_ИПДМ - передаточная функция сигнала измерительного преобразователя дифференциального манометра.

4 .  Модель измерительного устройства расхода газа (объект регулирования).

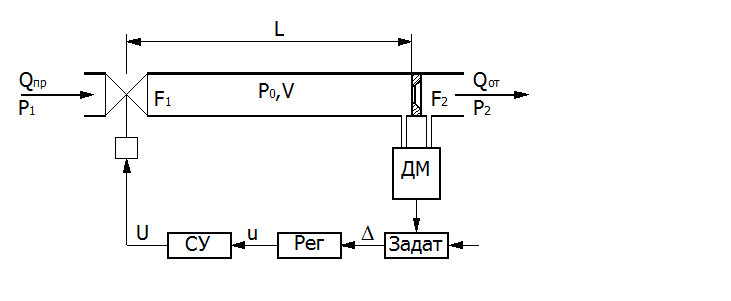
Рис. 1. Схема системы автоматического регулирования расхода газа.

Задачей автоматического регулирования является поддержание в заданных пределах значения расхода газа в магистрали, что можно обеспечить воздействием на линию притока газа.

Расход газа регулируется изменением проходного сечения крана F₁.