Модели объектов регулирования. Модели элементов систем автоматического регулирования, страница 4

Приток отток газа регулируются перемещением штоков кранов х₁, х₂ и, как следствие, изменением проходных сечений кранов F₁ и F₂ соответственно.

Газ под давлением р₁ большим критического (истечение сверхкритическое) поступает через кран сечением F₁ в ресивер объема V, где устанавливается давление Р и через кран сечением F₂ поступает к потребителю под давление р₂, меньшим критического (истечение докритическое).

Примем, что процесс осуществляется без теплообмена с внешней средой (адиабатный процесс). При этом в связи с тем, что давление газа в ресивере изменяется незначительно, температура газа в нем, при изменении давления, изменяется также незначительно.

Запишем балансовое уравнение.

В установившемся состоянии, когда имеется равенство поступающего Q_{пр 0} и расходуемого Q_от ­₀ количества газа в единицу времени, давление газа в ресивере остается постоянным (P = P₀).

                                                                                     (01)

где   Q_{пр 0} – расход газа на притоке, м³/с;

         Q_{от 0} – расход газа на оттоке, м³/с.

Вес газа G в объеме V равен

                                                                                        (02)

где   G – вес газа, кг;

         g - удельный вес газа, кг/м³;

         V – объем, м³.

При отклонениях притока и оттока газа от равновесных значений газ аккумулируется в ресивере или расходуется из него. Таким образом, давление в ресивере не остается постоянным. При изменении давления Р в ресивере постоянного объема V будет изменяться удельный вес газа g.

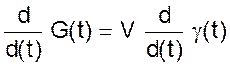                                                                      (03)

Если учесть некоторые внешние возмущения, связанные с изменением режимов работы потребителя газа и компрессора, то

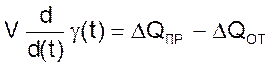                                                                (04)

Если обозначить через р_х  давление на входе в сужение (кран), а через р_у давление газа на выходе из него, то для докритического истечения можно записать

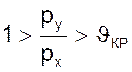,                                                                                   (05)

где 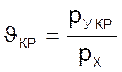     - критическое отношение давлений.

Приток газа в ресивер и отток из него определяется в этом случае соответственно зависимостями

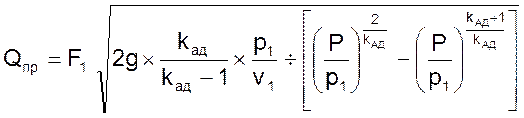                            (06)

и

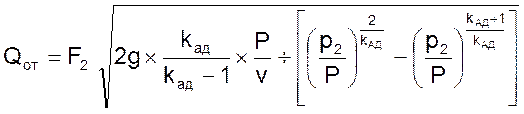                            (07)

где   F₁ и F₂ – эффективные площади проходных сечений кранов, м²;

         g – ускорение силы тяжести, м/с²;

         k_АД – показатель адиабаты;

         P – давление в ресивере, Па;

         v – удельный объем, м³/кг.

Так как между р₁ и v₁, а также между Р и V связь однозначна и выражается уравнением адиабатного процесса, можно составить две функциональные зависимости

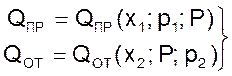                                                                      (08)

При надкритическом истечении газа, когда

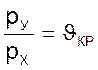   и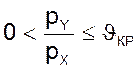  

приход и отток газа определяются соотношениями

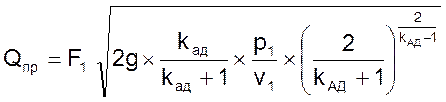                                       (09)

и

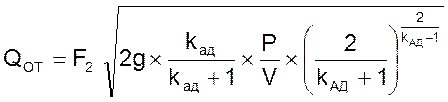,                                      (10)

следовательно функциональные зависимости приобретают вид

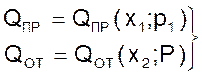                                                                          (11)

Для дальнейших рассуждений выбираем докритическое истечение газа

Структурная схема приведена на рис. 2.

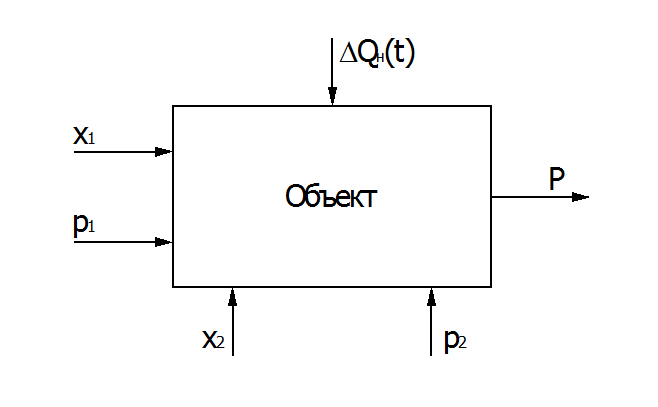
Рис. 2. Структурная схема объекта регулирования.

После разложения зависимостей 08 в ряд Тейлора и линеаризации для притока и оттока можно написать

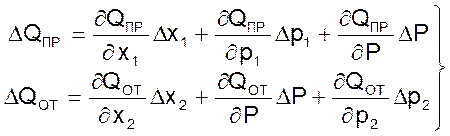                                      (12)

Учитывая также, что при адиабатном процессе (n = k_АД)

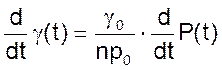
уравнение  04 можно записать в виде

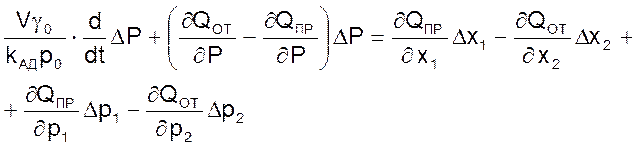            (13)

Выражение

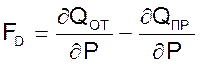                                                                          (14)

является фактором устойчивости ресивера.

Рассмотрим подробнее процесс подвода и отвода рабочего тела в ресивер. Начнем с того, что запишем статические характеристики системы

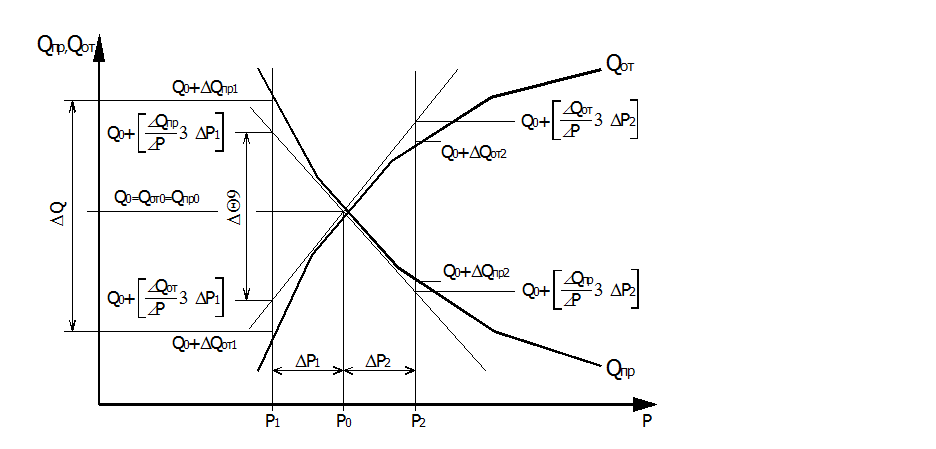
Рис. 3. Статические характеристики систем подвода рабочих тел в ресивер и отвода из него.

Из приведенного рисунка следует, что величина фактора устойчивости существенно положительна.

Введем относительные координаты

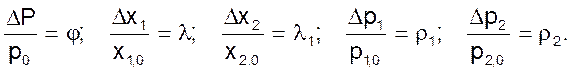
Тогда уравнение 13 можно записать в виде

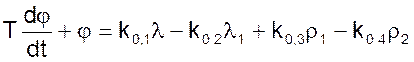                                            (15)

где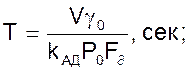                  

           

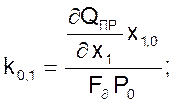
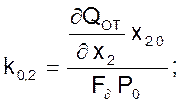
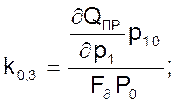
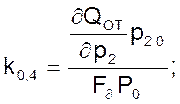
Если принять, что давления р₁ и р₂ неизменны, а также неизменно положение регулирующего органа х₂, то уравнение примет вид

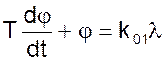                                                                               (16)

где   Т – постоянная времени ресивера.

8 .  Теоретическая модель резервуара.

Содержательное описание объекта.

Имеем емкость-накопитель кислоты, задача которой, в случае отказа подачи рабочего тела в линию, в течение определенного времени поддерживать поступление кислоты на вход последующего технологического аппарата. 

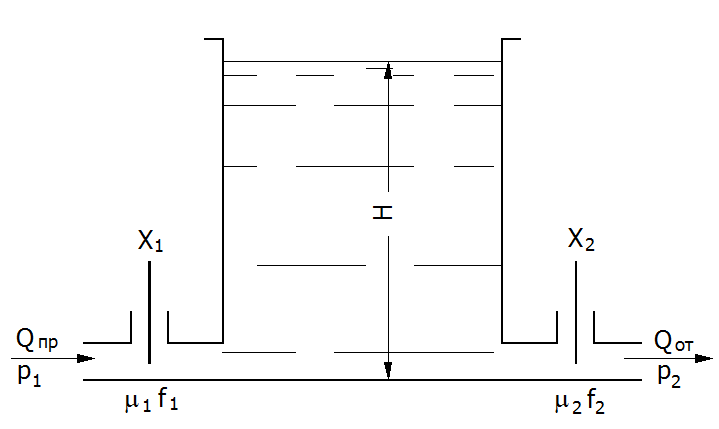
Объект регулирования - резервуар с линиями подвода и отвода жидкости.

Рабочее тело – кислота. Удельный вес  γ = 10240, [Н/м³].

Регулируемый параметр – высота жидкости в резервуаре.

Конструктивные параметры объекта:

Диаметр резервуара - 2 [м].

Высота резервуара - 10 [м].

Диаметр подводящей трубы d₁ = 0.1 [м].

Диаметр отводящей трубы d₂ = 0.15 [м].

Краны, расположенные на входе и выходе резервуара, имеют линейную расходную характеристику.

Номинальные  значения параметров процесса.

Давление на входе –   p_1,н = 21.58·10⁴, [Па].

Давление на выходе – p_2,н = 2.943·10⁴, [Па].

Коэффициент истечения для крана на входе μ_1,ном = 0.3.

Коэффициент истечения для крана на выходе μ_2,ном = 0.2.

Составление аналитической модели объекта.

Начнем с уравнения баланса для установившегося состояния притока и оттока жидкости в гидравлической системе. Будем считать, что это происходит при номинальных параметрах.

                                                                                    (01)