Правые составляющие уравнения разложим в ряд Тейлора и запишем
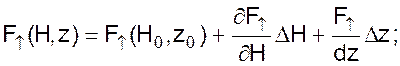
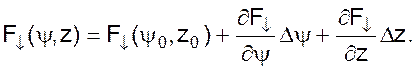
После подстановки последних двух уравнений в 09 и соответствующих преобразований получим
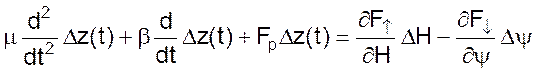 (10)
(10)
где μ – приведенная масса чувствительного элемента, кг;
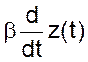 - сила гидравлического сопротивления
при движении поплавка (пропорциональна скорости перемещения);
- сила гидравлического сопротивления
при движении поплавка (пропорциональна скорости перемещения);
Введем относительные переменные:
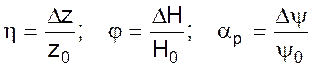 (11)
(11)
и разделим все члены уравнения на коэффициент при входной переменной
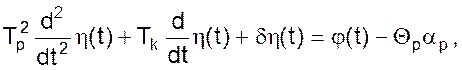 (12)
(12)
где 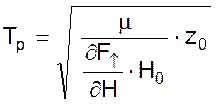 - время чувствительного
элемента, с;
- время чувствительного
элемента, с;
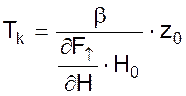 - время катаракта, с;
- время катаракта, с;
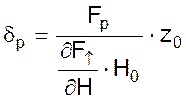 - степень
неравномерности;
- степень
неравномерности;
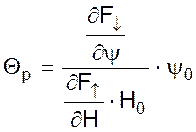 - фактор настройки
чувствительного элемента.
- фактор настройки
чувствительного элемента.
Математическая модель чувствительного элемента, представленного на рис. 2.
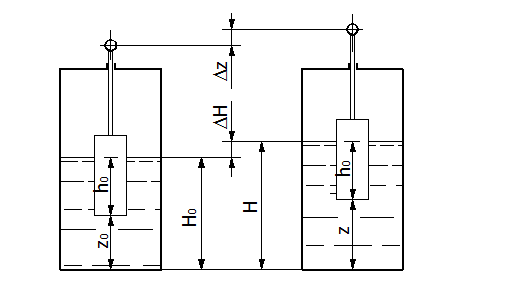
Рис. 2. Схема чувствительного элемента уровня поплавкового типа без пружины.
Составим уравнение баланса сил, действующих на поплавок чувствительного элемента в установившемся состоянии.
![]() (13)
(13)
где F↓ – восстанавливающая сила, Н;
F↑ - поддерживающая сила, Н.
Уравнение для восстанавливающей силы в этом случае может быть записано в виде
![]() (14)
(14)
где F↓ – восстанавливающая сила, Н;
Gп – вес поплавка, Н;
Таким образом, в данном случае восстанавливающая сила не зависит от перемещения поплавка.
По-прежнему будем считать уровень жидкости в емкости открытый.
Уравнение для поддерживающей (подъемной) силы поплавка F↑ будет иметь вид
![]() , (15)
, (15)
где γ – удельный вес жидкости, Н/м3;
S – площадь поперечного сечения поплавка, м2;
h – высота погруженной в жидкость части поплавка, м.
Уравнение статического равновесия с учетом представленных зависимостей примет вид
![]() (16)
(16)
Составим уравнение динамики для чувствительного элемента.
Из уравнения 15 следует в статике F↑= Const, F↓=Const
Запишем уравнение движения чувствительного элемента.
В процессе движения заглубление поплавка можно определить в виде разности между изменением уровня ΔН и перемещением поплавка Δz:
![]()
Поскольку в динамике ΔH ≠ Δz следовательно в динамике поддерживающая сила, зависит от перемещения, восстанавливающая же сила, определяемая весом поплавка Gп, остается постоянной.
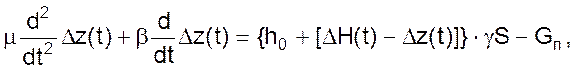 (17)
(17)
Зная, что h0ּγּS = Gп последнее уравнение можно представить в виде
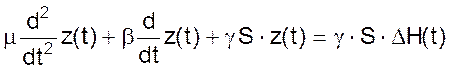
После перехода к относительным координатам (11) можно записать
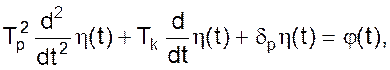 (18)
(18)
где 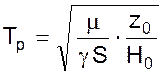 - время чувствительного
элемента, с;
- время чувствительного
элемента, с;
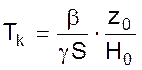 - время катаракта, с;
- время катаракта, с;
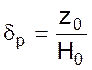 - степень неравномерности.
- степень неравномерности.
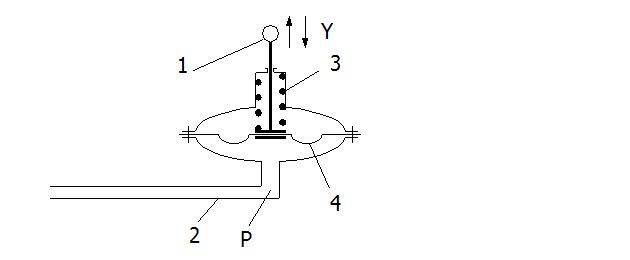
Рис. 1. Пневматический мембранный механизм с противодействующей пружиной.
1 – шток исполнительного механизма; 2 – пневмопровод; 3 – возвратная пружина; 4 – мембрана.
Звено производит операцию Р ® y: где Р – давление среды в мембранной камере, Па; у – перемещение штока исполнительного механизма, м.
Дифференциальное уравнение имеет вид:
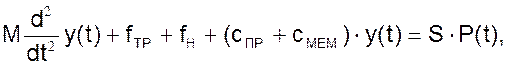 (01)
(01)
где М – масса движущихся частей, кг;
S – активная площадь мембраны, м2;
fТР – сила трения в сальнике, Н;
fН – равнодействующая неуравновешенных сил нагрузки, приложенных к штоку, Н;
Р – входной параметр (давление воздуха в мембранной камере), Па;
y – выходной параметр (перемещение штока), м;
сПР – жесткость противодействующей пружины, Н/м;
сМЕМ – жесткость мембраны, Н/м.
При конструировании МИМ разработчики стремятся сделать силы трения fТР и равнодействующую fН как можно меньше. У реальных МИМ эти параметры невелики и поэтому при расчетах параметры fТР и fН не учитывают. При указанных упрощениях собственная частота колебаний механизма равна
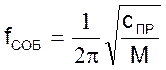 (02)
(02)
и для реальных приводов лежит в пределах 8…30 Гц. Это позволяет считать в обычных условиях (при достаточно медленных изменениях входного сигнала х) мембранные механизмы безинерционными звеньями.
В таком случае передаточная функция звена будет иметь вид:
![]() м3/Н, (03)
м3/Н, (03)
где 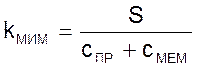 .
.
Пневмопровод длиной больше 5 метров можно рассматривать как звено первого порядка с транспортным запаздыванием
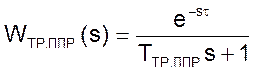 , (04)
, (04)
где ТТР.ППР - постоянная времени пневмопровода равна:
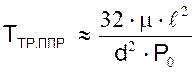 ,
,
где ℓ - длина трубы пневмопровода, м;
m
- динамическая вязкость воздуха, 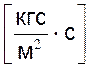 , (в технических
единицах вязкости);
, (в технических
единицах вязкости);
d – внутренний диаметр трубопровода, мм;
P0 – давление воздуха в пневмопроводе, кгс/см2.
Перевод технических единиц вязкости в единицы СИ
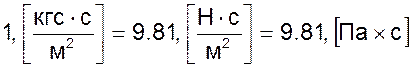
Перевод сПз в единицы СИ.
![]()
Для воздуха m
= 181310-7 ,[МПа.с] = 18.1, [Па.с] = 1.845, 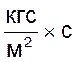 . (Краткий справочник по химии. Гороновский
И.Т. и др., Наукова думка, 1974, [712]).
. (Краткий справочник по химии. Гороновский
И.Т. и др., Наукова думка, 1974, [712]).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.