Файл САМРаботы02\САМ02a.doc 7 стр. 220 Кбайт
Раздел 1. Общий метод программирования уравнений, разрешенных относительно старшей производной.
1.1. Постановка задачи.
Пример 1.
Исследование полученной модели.
1.2. Задание для самостоятельного исполнения.
Пример 2.
В данной главе мы познакомимся с методами конструирования моделей средствами MATLAB-SIMULINK
Исследованию подлежит дифференциальное уравнение структурного типа, общий вид которого
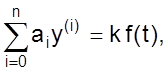(01)
где n – порядок производной;
yi – “i”-ая производная от искомой переменной;
f(t) – возмущение, действующее на систему;
аi, k – коэффициенты уравнений.
Имеется два алгоритма решения данного уравнения повысительный и понизительный (метод понижения порядка производной). Рассмотрим подробнее второй.
При понизительном алгоритме заданное уравнение разрешается относительно высшей (n-ой) производной и приобретает вид
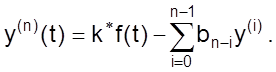(02)
где k* - коэффициент уравнения равный k* = k / an ;
bn-i – коэффициент уравнения равный bn-i = an-i / an .
Рассмотрим отдельно левую и правую части полученного уравнения.
Анализируя левую часть, можно предложить следующую схему ее решения. Принимаем, что значение функции y(n)(t) известно, тогда последовательным интегрированием получим все производные низших порядков, вплоть до получения в итоге (после n-ого интегрирования) искомой переменной y(t).
На модели данную операцию можно представить в виде цепочки модулей-интеграторов, количество которых равно порядку решаемого дифференциального уравнения.
Обратимся к правой части уравнения 02. Отметим, что она равна n-ой производной y(t). То есть можно утверждать, что, выполнив математические операции правой части уравнения, мы получим значение функции y(n)(t).
На модели данную операцию можно представить в виде модуля-сумматора, на вход которого поступает два слагаемых.
Первое слагаемое, представляет собой
возмущение, действующее на систему 
. На модели оно
может быть представлено при помощи специального модуля-источника возмущения.
Второе слагаемое представляет сумму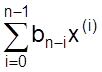 
,
включающую произведения искомой переменной и ее производных до (n –1) –ой степени включительно на коэффициенты
дифференциального уравнения, разрешенного относительно старшей производной.
На модели, составляющие второго слагаемого, могут быть представлены модулями-умножителями, на вход каждого из которых будут поступать значения коэффициентов bn-1 и значение производной x(i).
Значения производных до (n –1) –ой степени включительно на модели можно получить с выходов отдельных интеграторов левой части.
Рассмотренный алгоритм дает схему с кольцевой структурой, которая после установки начальных условий и ее возбуждении возмущением f(t), работает как единое целое, выдавая на выходе искомую функцию y(t), являющуюся результатом решения заданного уравнения.
Следует отметить, что использование в понизительном алгоритме интеграторов значительно уменьшает влияние различных помех на результаты решения.
Пример 1.
Разработать структурную схему для воспроизведения решения неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами
(П1.01)
и начальными условиями
используя средства пакета SIMULINK.
Напомним, мы ранее условились, что система визуального моделирования SIMULINK представляет собой библиотеку модулей математических операций преобразования сигнала.
Для решения поставленной задачи будем использовать метод понижения порядка производной. Разработку структурной схемы проводим в несколько этапов.
Этап I.
Разрешаем уравнение 03 относительно старшей производной
(П1.02)
Полученное уравнение представляет собой структурную схему, в которой каждой элементарной математической операции соответствует определенное звено.
Этап II.
Начнем с того, что средствами SIMULINK соберем блок-схему решения левой части уравнения П1.02, которая должна формировать сигналы производной и выходной переменной.
Представим ее в виде цепочки из двух интеграторов, в качестве которых используем модули Integrator [‘intigreitə] (Интегратор) из раздела Linear [‘ℓiniə] (Линейные элементы) библиотеки SIMULINK.
Сборку блок-схемы решения будем производить следующим образом. В библиотеке SIMULINK в соответствии со структурной схемой модели (в данном случае цепочки из двух интеграторов) отыскиваем нужный модуль и переносим его в окно-заготовку. Соединяя перенесенные блоки линиями передачи сигналов, в соответствии с логикой модели, формируем в окне-заготовке ее блок-схему.
Поскольку данная задача требует решения дифференциального уравнения с начальными условиями нам необходимо решить, будем ли мы использовать внутреннюю установку начальных значений интеграторов или внешнюю. Выберем внешнюю установку как более наглядную и настроим интеграторы на нее.
Для настройки интегратора ставим курсор на его пиктограмму и дважды щелкаем ЛКМ. В открывшемся окне настройки устанавливаем для параметра Initial condition source [i’niʃel kən’diʃen sɔ:s] (источник начального состояния) значение external [eks’tə:nl] (внешний). На пиктограмме интегратора появляется второй вход для задания начальных условий.
В качестве блоков задания начальных условий используем модули Constant [kɔnstənt] (Постоянная) из раздела Sources [sɔ:s] (Источники).
Сконструированная таким образом блок-схема решения левой части уравнения П1.02 представлена на рис. 1.
Соберем на ее базе подсистему, которую назовем «Левая», имея в виду решение левой части уравнения П1.02.
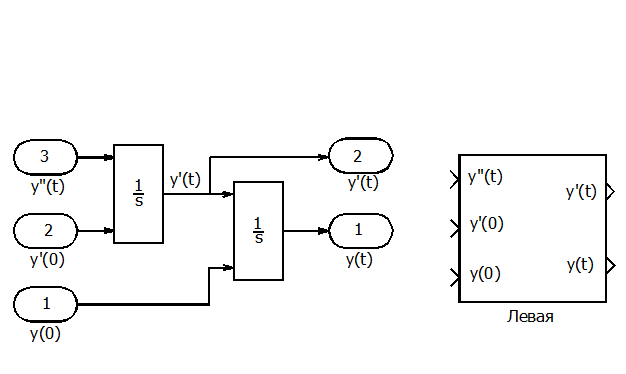
Рис. П1.1 Схема формирования сигналов производной и выходной переменной.
Этап III.
На третьем этапе разработаем блок-схему, которая воспроизводит правую часть уравнения П1.02. Для ее создания используем модули Sum [s∧m] (Сумма) из раздела Linear, Produkt [‘prod∧kt] (Умножить) из раздела Nonlinear и в качестве модели возмущения блок по выбору из раздела Sources [sɔs] (Источники).
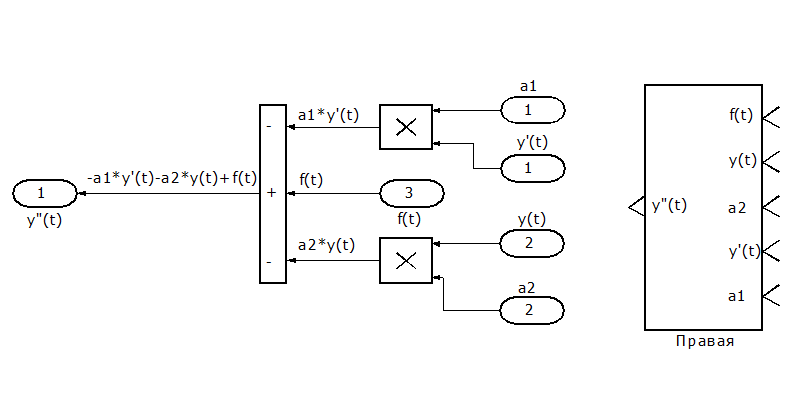
Рис. П1.2. Блок-схема формирования правой части уравнения П1.02.
Этап IV.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
