На последнем этапе создадим блок-схему решения заданного уравнения. С этой целью, объединим две последние блок-схемы. При этом с выходов интеграторов первой блок-схемы подадим сигналы y(t) и y’(t) на входы второй блок-схемы, а выходной сигнал второй блок-схемы y’’(t) на вход первой. Используя модуль Constant, будем задавать начальные условия. Для задания возмущения будем использовать блоки раздела Sources [so:s] – (Источники).
Для наблюдения за процессами решения к выходу первого и второго интеграторов подключим блок Scope [skəup] (Смотровое окно) радела Sinks [siŋks] (Получатели).
Используя блок Scope (настроив его на 2 канала), подключая их к разным точкам схемы, можно наблюдать, как изменяется скорость и выходная координата изучаемого процесса.
В некоторых случаях бывает целесообразно наблюдать не сами процессы в исследуемых системах, а их фазовые портреты. С этой целью можно заменить блок Scope в блок-схеме на блок XY Graph из того же раздела Sinks библиотеки SIMULINK. В последнем случае можно подавать на вход X значение исследуемого процесса y(t), а на вход Y – значение первой производной исследуемого процесса y’(t).
Исходное уравнение
y”(t) +a1*y’(t) +a2*y(t) = f(t).
Уравнение, разрешенное относительно высшей производной
y”(t) = f(t) -a1*y’(t) -a2*y(t).
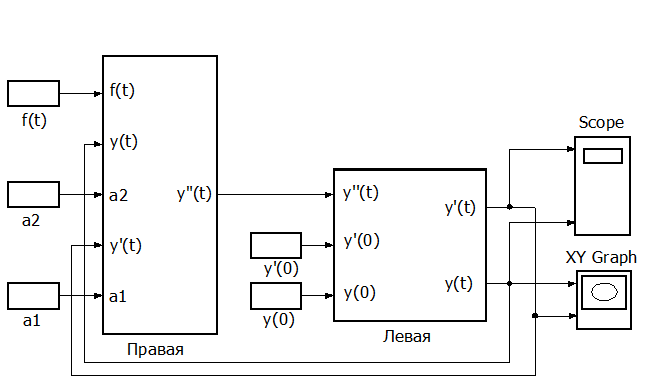
Рис. П1.3. Модель решения уравнения[1].
Чтобы подготовить модель к исследованию необходимо:
· определить вид и параметры возмущения, которое будем подавать на вход модели;
· установить значения начальных условий;
· установить значения коэффициентов уравнения;
· установить значение шага модельного времени;
· установить период моделирования.
Условимся:
· в качестве возмущения использовать единичную функцию h(t);
· принять величину начального значения y(0) = 1.0;
· принять величину начального значения y’(0) = 0.0;
· принять величину коэффициента a0 = 10;
· принять величину коэффициента a1 = 1;
· принять величину шага моделирования 0.001;
· принять период моделирования 0…20;
Настроим блоки модели в соответствии с выбранными значениями параметров и запустим модель на решение.
Получим решение данного уравнения. Проведем исследование решения при различных значениях параметров.
Набрать решение дифференциального уравнения
![]()
В качестве исходных значений для исследования примем:
коэффициент а0 = 10;
коэффициент а1 изменять в пределах 0.5…1.0 через 0.1;
начальные условия y\(0) = 0.0 и 2.0;
y(0) изменять в пределах 0.0…3 через 0.5;
возмущения, действующие на объект:
h(t) = 0.0 и 1.0;
f(t) = 2Sin5t.
Реализовать модель уравнения на ЭВМ. Провести исследование на этой модели и дать объяснение результатам наблюдений.
Пример 2.
Разработать программу для воспроизведения решения дифференциального уравнения
![]() (П2.01)
(П2.01)
с начальными условиями y(0) = y0, y\(0) = y0\ .
Программу строить на базе пакета SIMULINK.
Для того чтобы проиллюстрировать гибкость SIMULINK решим эту задачу при помощи несколько иной блок-схемы решения.
Для решения поставленной задачи будем опять использовать метод понижения порядка производной. Разработку структурной схемы проводим в несколько этапов.
Этап I.
На первом этапе разрешим данное уравнение относительно старшей производной
![]() (П2.02)
(П2.02)
Этап II.
На втором этапе собираем часть структурной схемы, которая должна формировать сигналы производных и выходной переменной. Представим ее в виде цепочки из двух интеграторов и объединим эту цепочку в подсистему
Поступим следующим образом. Перенесем в окно-заготовку два интегратора из раздела Linear библиотеки SIMULINK. Настроим их аналогично первому примеру. Соединим линией связи в соответствии с логикой их работы в модели. Выделим при помощи рамки блоки и соединяющие их линии связи. Активизируем команду Create Subsystem из меню Edit. В результате SIMULINK заменит выделенные блоки одним блоком Subsystem.
Посмотрим и отредактируем (разметим) содержимое полученного блока. Начнем с того, что поставим курсор на изображение блока и дважды щелкнем ЛКМ. В открывшемся окне видно, что SIMULINK добавил в схему еще два модуля In и Out из раздела библиотеки Connections, представляющие входы и выходы в систему высшего уровня. Теперь разметим линию связи, а также входы и выходы данной подсистемы в соответствии с рис. 1.
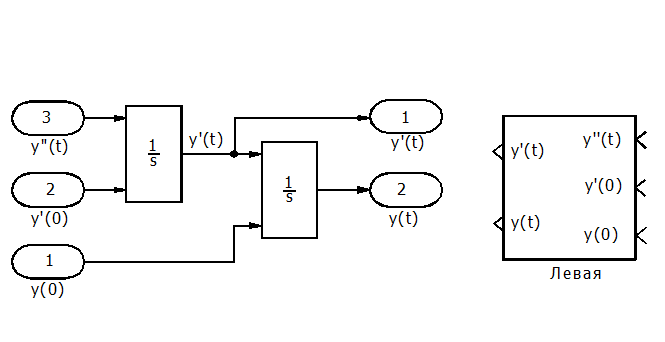
Рис. П2.1. Схема формирования сигналов производной и выходной переменной.
Этап III.
На третьем этапе разрабатываем схему, которая воспроизводит правую часть уравнения.
Блок-схема формирования правой части уравнения представлена на рис. П2.2. В ней использованы модули Product [‘prod∧kt] (Умножить) из раздела Nonlinear и блок Sum из раздела Linear. Блоки In и Out SIMULINK присоединит автоматически при создании подсистемы.
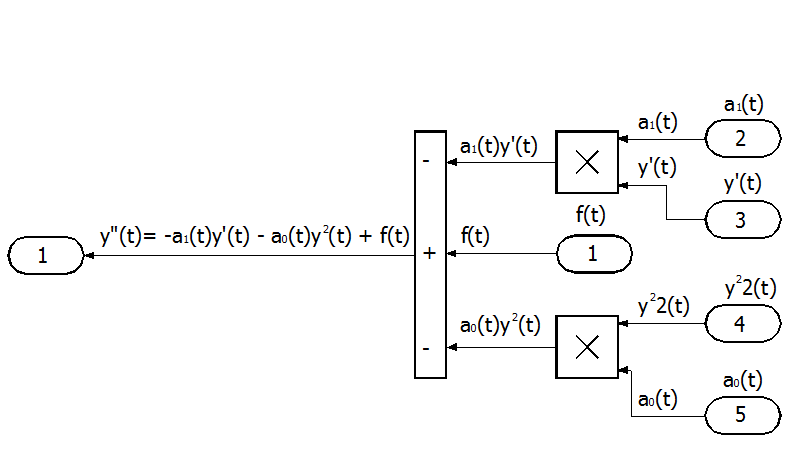
Рис. П2.2. Блок-схема формирования правой части уравнения.
Объединим представленную блок-схему в подсистему и отредактируем ее в соответствии с рис. 2.
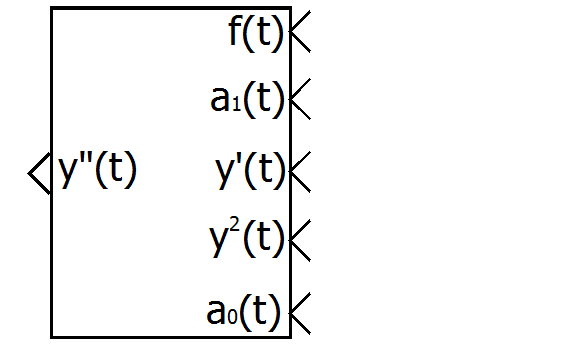
Рис. П2.3. Подсистема формирования правой части уравнения.
Для создания блоков переменных коэффициентов a1(t) и a0(t) будем использовать модули Fcn [‘f∧ ŋkʃen] (Функция) из раздела библиотеки Nonlinear [non‘ℓiniə] (Нелинейные элементы), а в качестве генераторов времени модули Clock [clɔk] (Часы) из раздела библиотеки Sources.
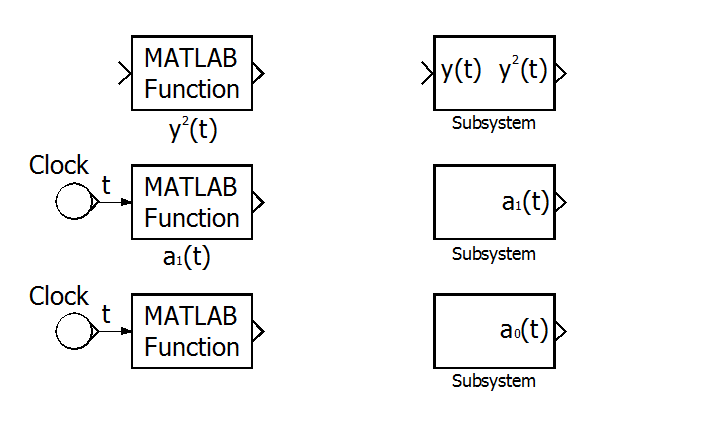
Рис. П2.4. Подсистемы формирования коэффициентов уравнения.
Из полученных подсистем сформируем блок-схему решения данного уравнения. Для наблюдения решения будем использовать модуль Scope из библиотеки Sinks. Начальные условия будем задавать при помощи блоков Нач. 1 и Нач. 2, сформированных из модулей Constant раздела Sources библиотеки SIMULINK. Возмущение f(t) - при помощи модуля из этой же библиотеки или можем сформировать его специально.
Уравнение, разрешенное относительно старшей производной
![]()
Subsystem – подсистема формирования производной и выходной переменной.
Subsystem 1 – подсистема формирования правой части уравнения.
Коэффициенты уравнения приняты: а1(t) = t * 2; a0(t) = t * 2
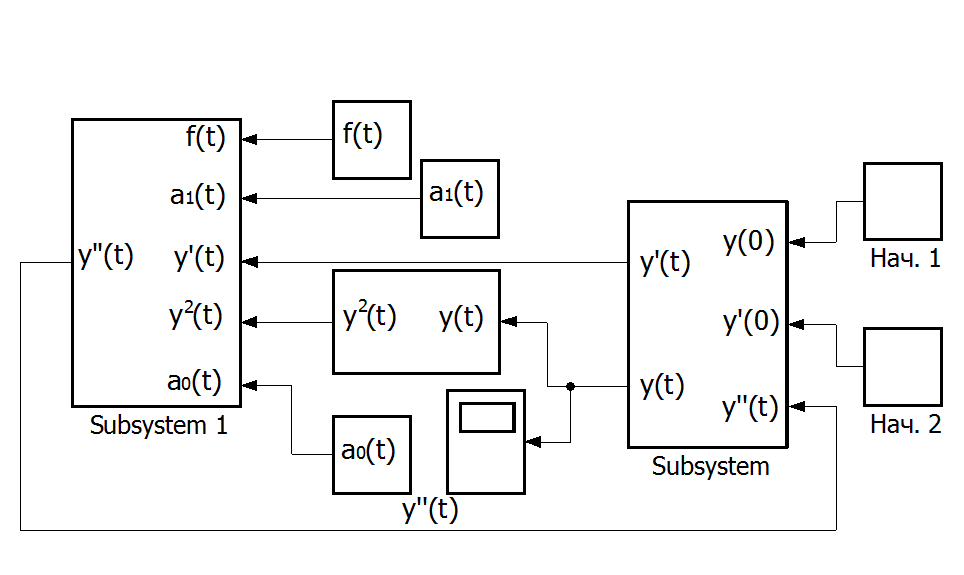
Рис. П2.5. Блок-схема решения заданного уравнения[2].
[1] Программа записана в файле Мои документы\ПрогSim\ПосГлава1\gla1_02_p1ris3.mdl
[2] Программа записана в файле «Мои документы\ПрогSIM\ПосГлава1\gla1_02 p2ris5»
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.