Файл Модели\САМРаботы02\САМ06а.doc 5 стр. 200 Кбайт
Пример 7.
Пусть, к примеру, требуется решить линейное дифференциальное уравнение второго порядка с правой частью
![]() . (П7.01)
. (П7.01)
При использовании SIMULINK это уравнение можно решить несколькими способами.
Первый способ решения.
а) Разрабатывается блок-схема решения с использованием в качестве задатчиков коэффициентов уравнения модулей Gain раздела Linear. Начнем с того, что разрешим его относительно второй производной
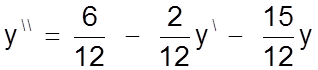 (П7.02)
(П7.02)
Полученное решение в модулях SIMULINK можно изобразить в виде
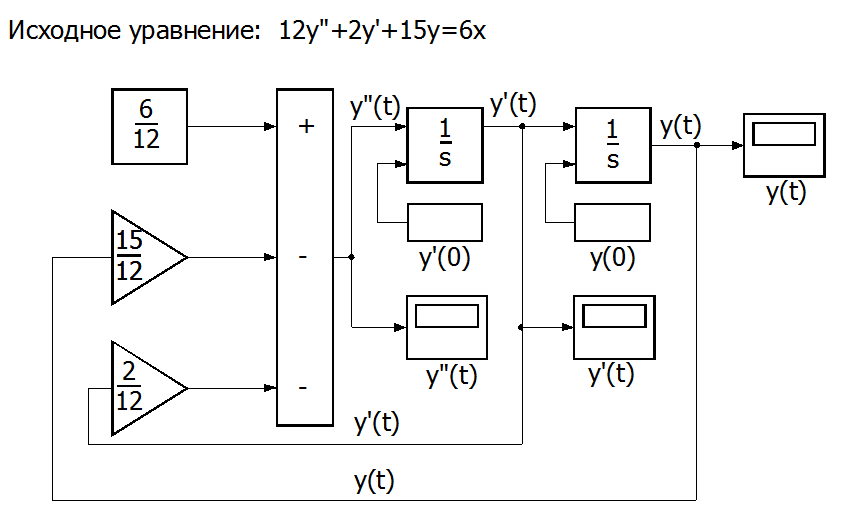
Рис. П7.1 Блок-схема решения с использованием в качестве задатчиков коэффициентов уравнения модулей Gain[1].
Для решения уравнения нами использованы 2 интегратора, 1 сумматор и 2 усилителя из раздела Linear библиотеки SIMULINK.
Вторая производная, согласно П7.02, должна получится путем вычитания из y0 равного 6/12, производных, умноженных на соответствующие коэффициенты.
Вид и значение параметров решения можно наблюдать на экране блока Scope раздела Sinks [siŋks - получатели] «y(t)».
b) Блок-схема решения с использованием в качестве задатчиков коэффициентов уравнения блоков Constant раздела Sources библиотеки SIMULINK и организации решения правой части уравнения в виде подсистемы.
Решение левой части уравнения по-прежнему представим в виде цепочки двух интеграторов, соединенных последовательно.
Для решения правой части уравнения соберем из модулей SIMULINK блок-схему и преобразуем ее в подсистему.
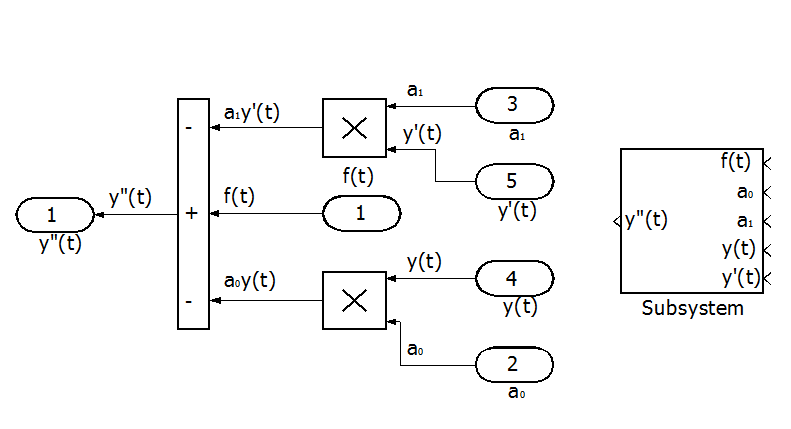
Рис. П7.2. Блок-схема решения правой части уравнения.
Составим блок-схему решения уравнения с использованием подсистемы.
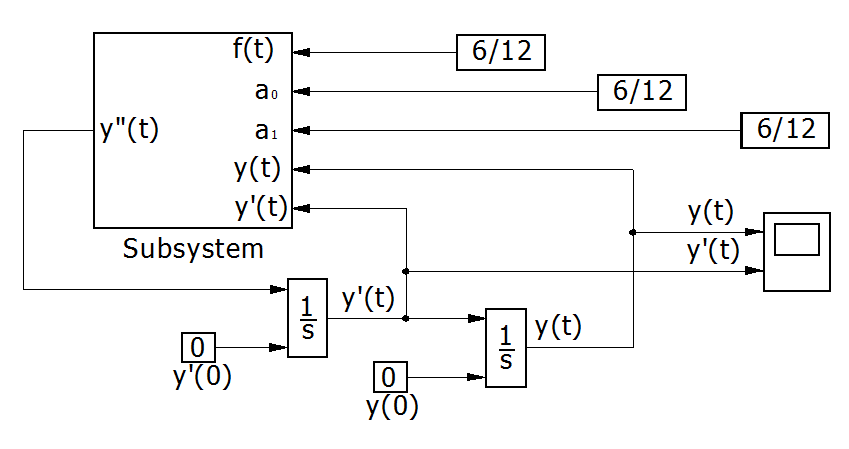
Рис. П7.3. Блок-схема решения с использованием в качестве задатчиков коэффициентов уравнения модулей Constant[2].
Второй способ решения.
Используя SIMULINK, можно представить другой способ решения этого уравнения. Решение можно получить, используя модуль Transfer Fcn [‘trænsfə: Fkn] (Передаточное звено). В качестве входного сигнала будем использовать блок Constant раздела Sources [so:s - источники]
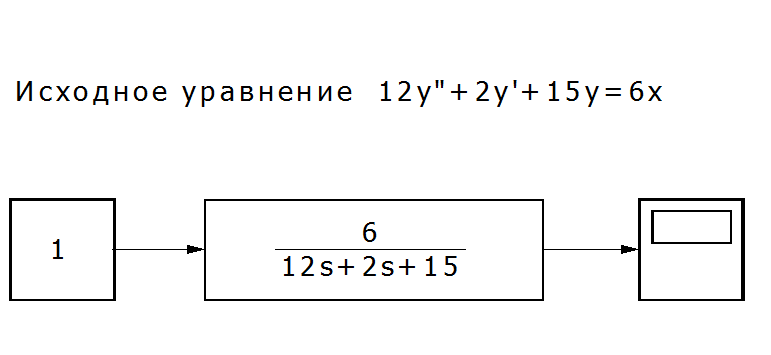
Рис. П7.4. Решение уравнения с использованием типовых структурных схем[3].
Вид и значение параметров решения можно наблюдать на экране блока Scope раздела Sinks [siŋks - получатели] «Интеграл».
Третий способ решения.
SIMULINK может предложить еще один способ решения данного дифференциального уравнения. Воспользовавшись методами структурных преобразований, данное уравнение можно представить в виде структурной схемы, состоящей из типовых модулей.
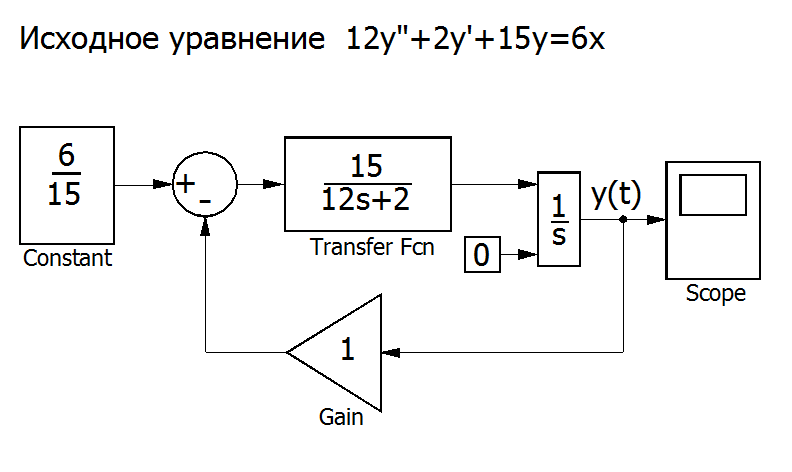
Рис. П7.5. Решение уравнения с использованием структурных преобразований[4].
Пример 8.
Проведем исследование дифференциального уравнения 2 порядка
![]() (П8.01)
(П8.01)
методами фазовой плоскости, используя возможности SIMULINK.
Начнем с того, что разрешим уравнение относительно старшей производной.
![]() (П8.02)
(П8.02)
где a1 = 2e/T; a0 = 1/T2; x1(t) = x(t)/T2.
Решение левой части уравнения представим в виде цепочки из двух интеграторов соответственно настроенных.
Для решения правой части уравнения создадим 2 подсистемы. Одну для формирования значений коэффициентов уравнения, разрешенного относительно старшей производной и вторую для решения собственно правой части уравнения.
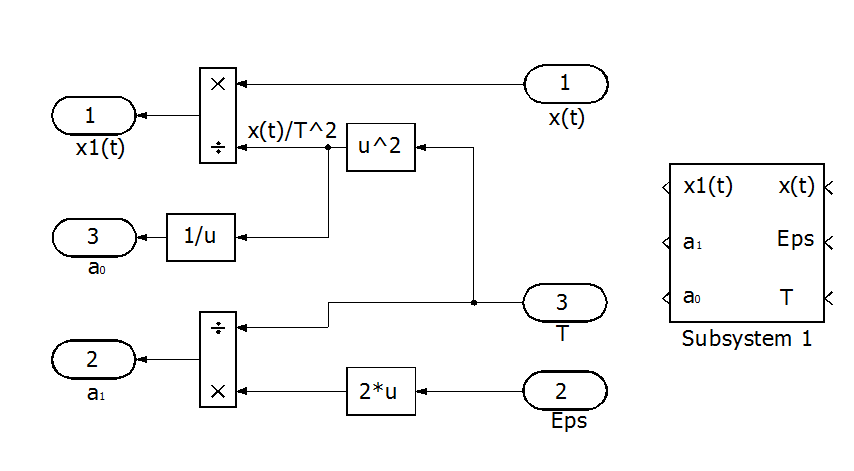
Рис. П8.1 Блок-схема формирования коэффициентов уравнения.
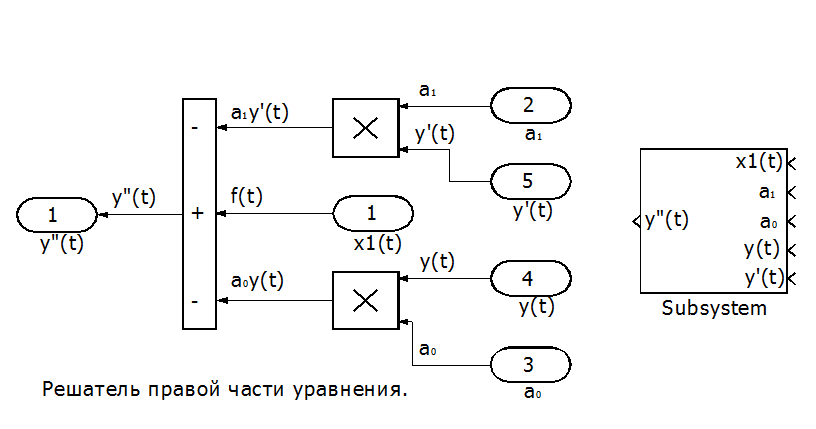
Рис. П8.2. Решатель правой части уравнения.
Решение дифференциального уравнения с учетом созданных подсистем будет иметь вид
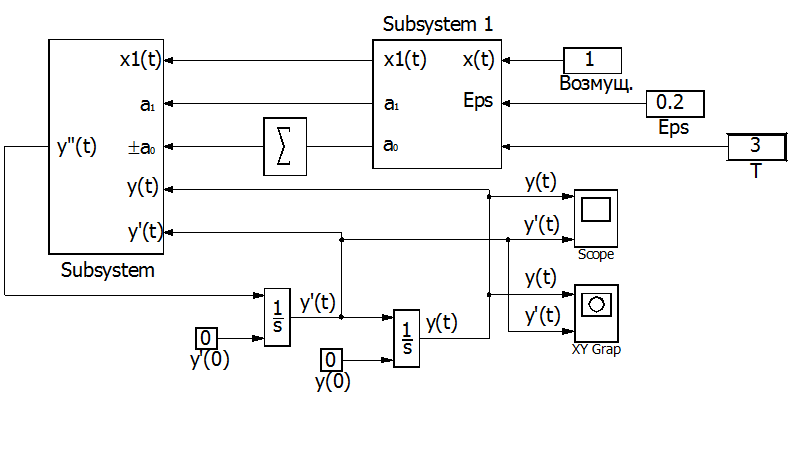
Рис. П8.3. Блок-схема решения дифференциального уравнения[5].
Исследование фазового портрета.
Для наблюдения за фазовыми траекториями включим в качестве смотрового окна в блок-схему решения уравнения рис. П7.3 дополнительно модуль XY Graph из раздела Sinks библиотеки SIMULINK.
Сущность метода фазовой плоскости заключается в построении фазовых траекторий по дифференциальным уравнениям в системе координат: ось x - значение исследуемой величины u, ось y – скорость ее изменения du/dt. Процесс изменения траектории представляет собой движение изображающей точки на фазовой плоскости. Начальные условия определяют первоначальное положение изображающей точки на фазовой плоскости. Совокупность фазовых траекторий в плоскости (x, y) носит название фазовый портрет. Подробнее с методами фазовой плоскости можно ознакомиться по «Иващенко Н.Н. Автоматическое регулирование. Теория и элементы систем. Учебник для вузов. Изд. 4-е, перераб. и доп. М., «Машиностроение», 1978. Стр. 485-495».
Задачей нашего исследования является построение некоторых наиболее характерных фазовых портретов.
Рассмотрим следующие случаи характерные для уравнения 2 порядка:
▪ e = 0; 0 < e < 1; -1 < e < 0;
▪ e > 1; e < -1; e = 0.
Кроме этого рассмотрим, как будут изменяться фазовые траектории при изменении начальных условий.
На этом знакомство с методами решения дифференциальных уравнений в среде SIMULINK будем считать законченным.
[1] Программа расположена на файле «Мои документы\ПрогSIM\ПосГлава1\gla1_06 p7ris1»
[2] Программа расположена на файле «Мои документы\ПрогSIM\ПосГлава1\gla1_06 p7ris3»
[3] Программа расположена на файле «Мои документы\ПрогSIM\ПосГлава1\gla1_06 p7ris4»
[4] Программа расположена на файле «Мои документы\ПрогSIM\ПосГлава1\gla1_06 p7ris5»
[5] Программа расположена на файле «Мои документы\ПрогSIM\ПосГлава1\gla1_06 p8ris3»
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.