Файл САМРаботы02\САМ03а.doc 4 стр. 2.74 МБ
1.1. Решение системы дифференциальных уравнений с начальными условиями.
1.2. Решение линейного дифференциальное уравнение четвертого порядка с правой частью
Пример 3.
Решить систему дифференциальных уравнений
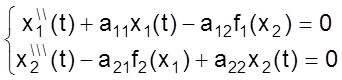 ,
,
с начальными условиями
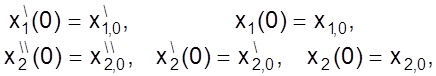
Перед нами нелинейная система дифференциальных уравнений. Первое из них уравнение второго порядка. Второе уравнение третьего порядка. Нелинейность обусловлена наличием двух функций f1(x2) и f2(x1).
Этап I.
Разрешим оба уравнения относительно переменной старшего порядка
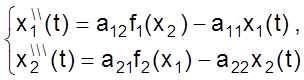
Этап II.
Составим две цепочки из последовательно включенных интеграторов. Для первого уравнения двух, второго – трех, в соответствии с порядком уравнений.
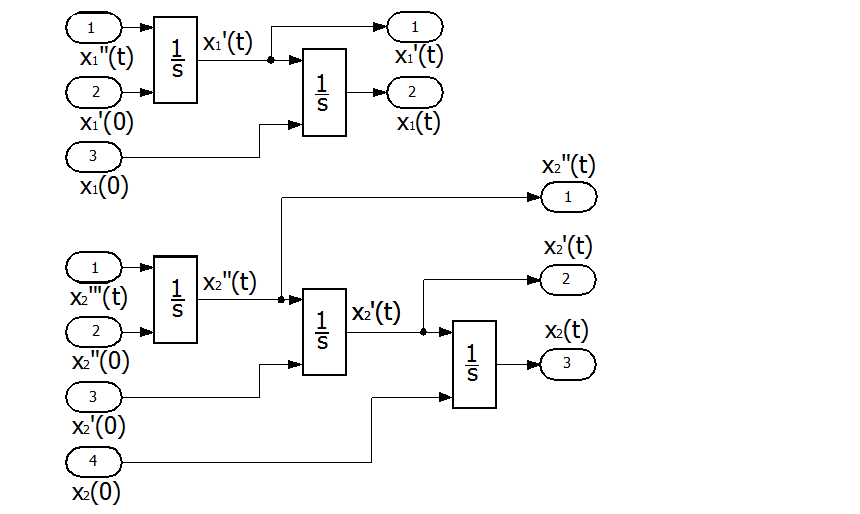
Рис. П3.1. Цепочки интеграторов.
Превратим их в подсистемы.
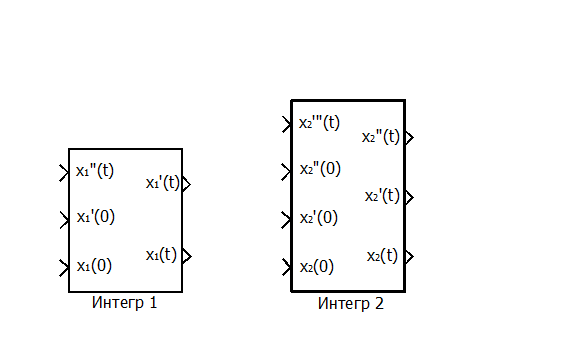
Рис. П3.2. Подсистемы «Интеграторы» уравнений.
После создания подсистем их необходимо открыть и разметить. Обозначить блоки In и Out именами в соответствии с рис. 2.
Этап III.
На третьем этапе разработки модели системы дифференциальных уравнений сформируем блок-схемы правых частей этих уравнений. При формировании блок-схем правых частей уравнений мы будем использовать модули Sum и Product.
Выберем эти модули из соответствующих разделов библиотеки, перенесем их в окно-заготовку и соединим линиями связи в соответствии с логикой работы модели. Для удобства их дальнейшего использования превратим эти блок-схемы в подсистемы.
Выделим при помощи рамки блок-схемы правых частей уравнений и воспользуемся командой Create Subsystem из меню Edit.
Откроем образованные подсистемы и разметим их. Модули In и Out SIMULINK присоединит автоматически при формировании подсистем из блок-схем.
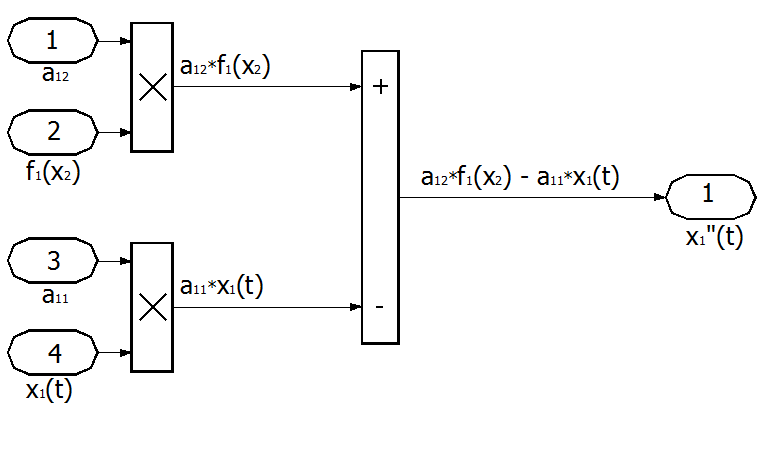
Рис. П3.3а. Блок-схема правой части первого уравнения.
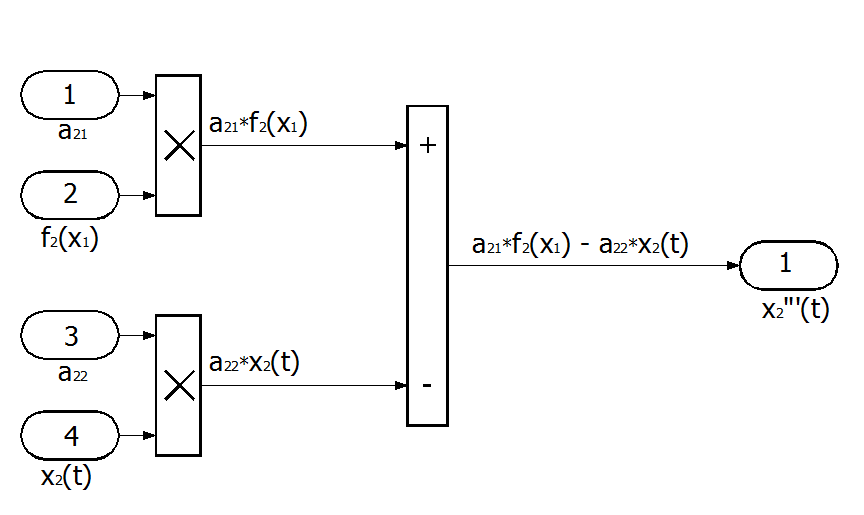
Рис. П3.3б. Блок-схема правой части второго уравнения.
Вид подсистем, созданных из блок-схем правых частей уравнений, представлен на рис. П3.4.
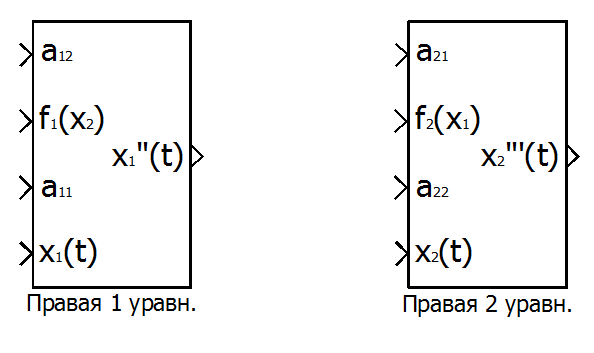
Рис. П3.4. Подсистемы правых частей уравнений.
Этап IV.
Произведем замыкание обратных связей, соответствующих правым частям уравнений (объединим созданные подсистемы) и получим блок-схему модели решения системы дифференциальных уравнений.
Разрешенная относительно старшей производной система уравнений.
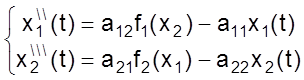
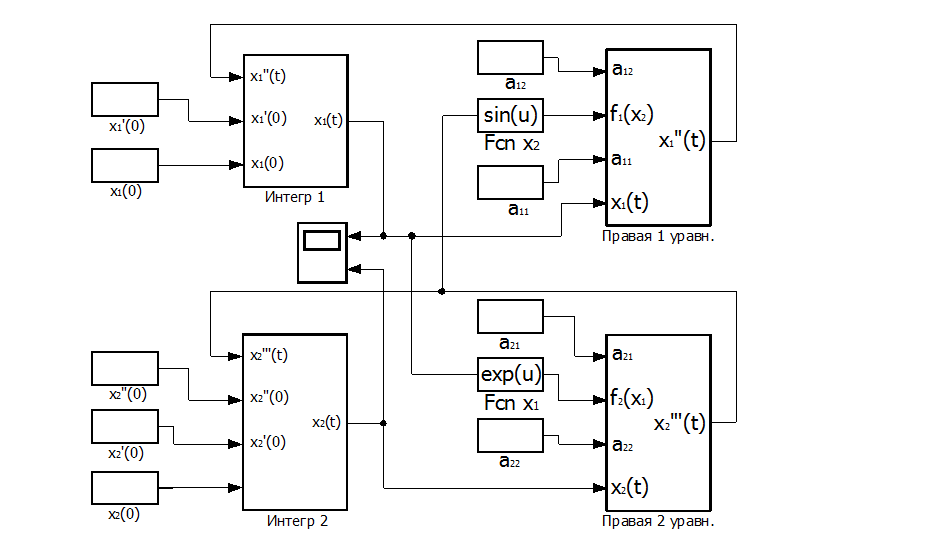
Рис. П3.5. Блок-схема модели решения системы дифференциальных уравнений[1].
Пример 4.
Пусть, к примеру, требуется решить линейное дифференциальное уравнение четвертого порядка с правой частью
![]() (02)
(02)
Соберем это решение в модулях SIMULINK.
Этап 1.
Начнем с того, что разрешим его относительно старшей производной
![]() (03)
(03)
Этап II.
Для решения левой части уравнения составим цепочку из 4 последовательно соединенных интеграторов.
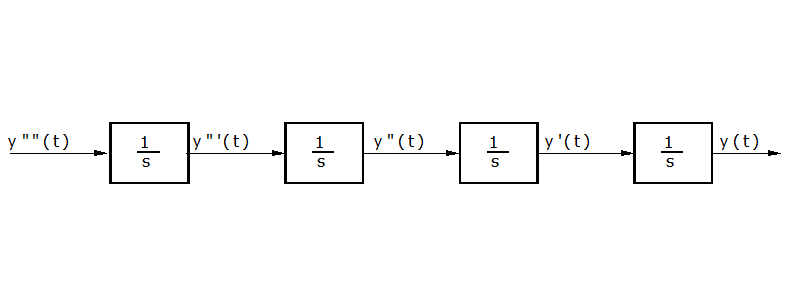
Рис. П4.1. Цепочка интеграторов.
Этап III.
На третьем этапе сформируем блок-схему правой части уравнения.
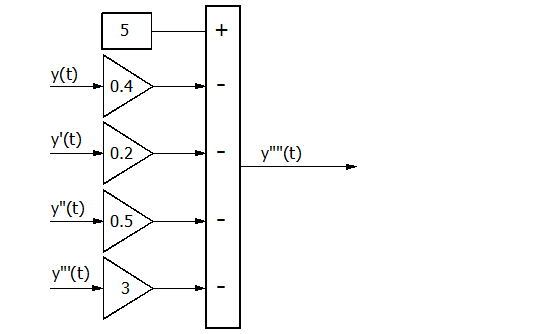
Рис. П4.2. Блок-схема решения правой части уравнения.
Этап IV.
Произведем замыкание обратных связей, соответствующих правой части уравнения и получим блок-схему модели решения системы дифференциальных уравнений.
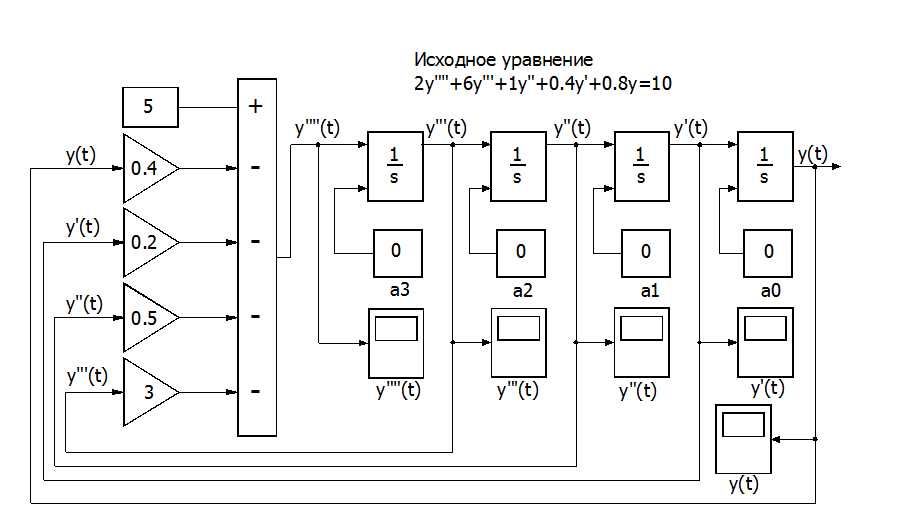
Рис. П4.3. Блок-схема модели линейного дифференциального уравнения[2].
Для решения дифференциального уравнения нами использованы 4 интегратора, 1 сумматор и 4 усилителя и из раздела Linear библиотеки SIMULINK и один источник возмущения, в качестве которого использован модуль Constant из раздела библиотеки Sources.
[1] Программа расположена на файле «Мои документы\ПрогSIM\ПосГлава1\gla1_03 p3ris5»
[2] Программа расположена на файле «Мои документы\ПрогSIM\ПосГлава1\gla1_03 p4ris3»
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.