Пункты производства обладают запасом некоторого
продукта - ai, i = 1, I;
Пункты потребления имеют потребности в определенном продукте - bj, j=1, J.
Минимизировать общую стоимость перевозок между пунктами производства и потребления в количестве хij при известных «тарифах на перевозки между пунктами производства и потребления — сij. Для пунктов производства существуют ограничения на объем производства, для пунктов потребления - ограничения объем спроса продукта.
Математическая форма записи транспортной задачи:
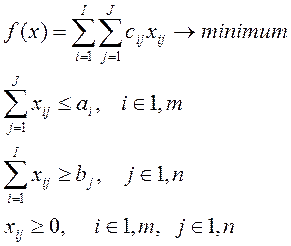
Для сбалансированной транспортной задачи выполняется соотношение равенства суммы запасов сумме потребностей:
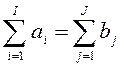
Схема расположения исходных данных на листе рабочей книги — рис. 8. Для удобства создания модели создаются именованные блоки данных (табл. 5).
Рис. 8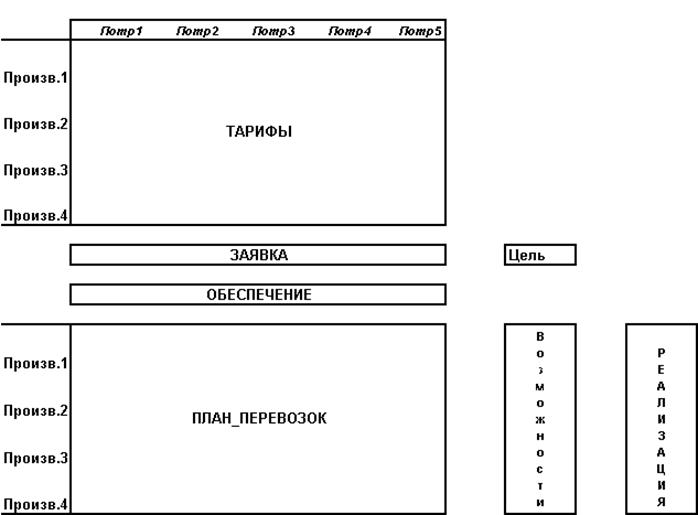
Таблица 5
|
№ п/п |
Название блока |
Тип блока |
Примечание |
|
1 |
ТАРИФЫ |
Матрица |
Размер — |
|
2 |
ЗАЯВКА |
Вектор-строка |
Размер — |
|
3 |
ОБЕСПЕЧЕНИЕ |
Вектор-строка |
Размер — |
|
4 |
ВОЗМОЖНОСТИ |
Вектор-столбец |
Размер — |
|
5 |
РЕАЛИЗАЦИЯ |
Вектор-столбец |
Размер — |
|
6 |
ЦЕЛЬ_Т |
Ячейка |
Целевая функция |
|
7 |
ПЛАН_ПЕРЕВОЗОК |
Матрица |
Результат
решения задачи |
Пример 24. Решение транспортной задачи
Определить оптимальные план перевозок между оптовыми базами («производители») и магазинами («потребители»):
§ тарифный план перевозок - табл.6:
Таблица 6
|
Магазин 1 |
Магазин 2 |
Магазин 3 |
Магазин 4 |
|
|
База 1 |
2,60р. |
3,00р. |
2,00р. |
7,00р. |
|
База 2 |
8,00р. |
3,00р. |
2,00р. |
2,00р. |
§ заявки магазинов - табл.7:
Таблица 7
|
Магазин 1 |
Магазин 2 |
Магазин 3 |
Магазин 4 |
|
120 |
200 |
180 |
450 |
§ возможности оптовых баз - табл. 8:
Таблица 8
|
База 1 |
500 |
|
База 2 |
450 |
Последовательность действий:
1. Открыть рабочую книгу MATSTAT.xls.
2. Перейти на лист — ПОИСК РЕШЕНИЯ2.
3. Ввести исходные данные и подготовить именованные блоки согласно табл. 5.
4. Ввести формулу для вычисления целевой функции:
=СУММПРОИЗВ(ТАРИФЫ;ПЛАН_ПЕРЕВОЗОК)
5. Ввести формулы в первую ячейку блока ОБЕСПЕЧЕНИЕ — суммирование ячеек первого столбца блока ПЛАН_ПЕРЕВОЗОК:
=СУММ(B28:B29).
Размножить формулу по ячейкам блока ОБЕСПЕЧЕНИЕ.
6. Ввести формулы в первую ячейку блока РЕАЛИЗАЦИЯ — суммирование ячеек первой строки блока ПЛАН_ПЕРЕВОЗОК: =СУММ(B28:E28).
Размножить формулу по ячейкам блока РЕАЛИЗАЦИЯ.
7. Ввести формулы для вычисления итогов по блокам ВОЗМОЖНОСТИ и ПОТРЕБНОСТИ. Если значения итогов не совпадают, исправить ошибки.
8. Выполнить команду Сервис, Поиск решений, сформировать модель:
установить целевую ячейку — блок ЦЕЛЬ_Т, минимум
изменяя ячейки — ПЛАН_ПЕРЕВОЗОК;
ограничения:
ОБЕСПЕЧЕНИЕ >= ЗАЯВКА
ПЛАН_ПЕРЕВОЗОК = целое
ПЛАН_ПЕРЕВОЗОК >= 0
РЕАЛИЗАЦИЯ <= ВОЗМОЖНОСТИ
задать настройку алгоритма нахождения оптимального решения;
нажать кнопку Выполнить;
сформировать отчет Результаты;
выполнить анализ полученного решения.
9. Изменить условия задачи и повторить решение.
10. Сохранить рабочую книгу MATSTAT.xls.
В начало ...
ВНИМАНИЕ. После завершения работы проверить наличие файлов:
|
Файл (имя в задании) |
|
MATSTAT.xls |
|
Описательная статистика |
Прогнозирование значений случайной величины |
|
Подготовка данных статистических моделей |
Скользящее среднее |
|
Функции СЛЧИСЛ, СЛУЧМЕЖДУ |
Экспоненциальное сглаживание |
|
Генерация случайных чисел в Пакете анализа |
Статистический анализ и обработка данных в MS Excel выполняются с помощью встроенных функций категории Статистические и специализированных информационных технологий Пакета анализа. Наиболее часто применяются методы описательной статистики для массивов значений показателей (выборок) и прогнозирование значений для временных рядов.
Для массивов значений показателей вычисляются статистические характеристики.
1. Средние оценки:
![]() средняя арифметическая — математическое ожидание случайной
величины, функция СРЗНАЧ;
средняя арифметическая — математическое ожидание случайной
величины, функция СРЗНАЧ;
![]() средняя геометрическая — оценка средних темпов роста, поиск
значения, равноудаленного т других значений, функция СРГЕОМ;
средняя геометрическая — оценка средних темпов роста, поиск
значения, равноудаленного т других значений, функция СРГЕОМ;
![]() средняя гармоническая — оценка средней суммы обратных величин,
функция СРГАРМ.
средняя гармоническая — оценка средней суммы обратных величин,
функция СРГАРМ.
Между средними существует соотношение:
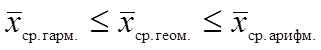
2. Показатели вариации:
- общее число значений в массиве, функция СЧЕТ;
- сумма значений переменных в массиве, функция СУММ;
- дисперсия случайной величины - характеризует рассеивание значений случайной величины относительно средней арифметической, функции:
ДИСП (дисперсия по выборке)
ДИСПР (по генеральной совокупности);
- стандартное отклонение - корень квадратный из дисперсии, функция:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.