Модуль "Математические и статистические методы анализа данных в MS Excel", страница 3

	A	B	C	D	E	F	G
39	15,25р.	50	55	60	70	80	95
40	1000
41	1020
42	1040
43	1060
44	1080
45	1100
46	1120
47	1140
48	1160
49	1180
50	1200

Рис. 2

Массив формул: {=ТАБЛИЦА(В7;B6)}. Можно изменить значение объема выпуска (ячейки А40:А50), вероятность реализации продукции - (B39:G39) или формулу (ячейка A39).

6.  С помощью команды Формат, Условное форматирование для ячеек в диапазоне В40:G50 выделить другим цветом ячейки, значение которых отрицательно. Проанализировать область положительных и отрицательных значений прибыли на единицу продукции.

7. Построить диаграмму (тип — Точечная) для зависимости прибыли на единицу продукции от вероятности реализации, фиксированный объем выпуска — 1200:

§  выделить диапазон ячеек B50:G50;

§  команда Вставка, Диаграмма, тип — Точечная, вид — сглаживающие линии с маркерами;

§  имя ряда — Объем выпуска 1200, значения Х — ячейки B39:G39;

§  легенды нет, подписи — значение Y, заголовки: название диаграммы — «Объем выпуска 1200 шт.», Ось Х — «Вероятность реализации, %», ось Y — «Прибыль на единицу продукции»;

§  разместить диаграмму на отдельном листе.

8.  Внести изменения в таблицу исходных данных (объем выпуска, вероятность реализации, %), просмотреть изменения диаграммы.

9.  Сохранить рабочую книгу MATSTAT.xls.

В начало...

ВНИМАНИЕ. После завершения работы проверить наличие файлов:

Модуль "Математические и статистические методы анализа данных в MS Excel"

Подбор параметра

Подбор параметра — информационная технология, используемая  для быстрого ответа на вопрос «Какое значение аргумента обеспечивает получение заданного значения функции?».

Исследование выполняется для ячеек, содержащих формулы. С помощью команды Сервис, Зависимости формул, Влияющие ячейки для каждой такой ячейки изображается зависимость от ячеек, которые содержат ее аргументы. На рис. 1 представлена расчетная модель (см. Пример 23) с измененным положением ячеек для лучшего изображения их связей; ячейки, содержащие формулы, затенены.

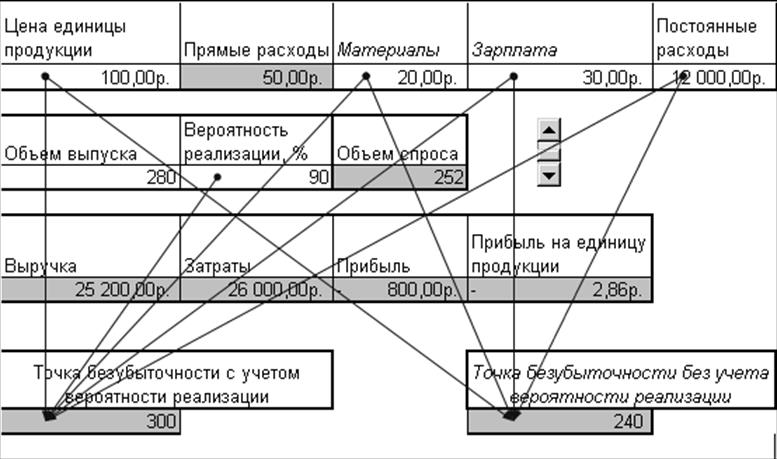
Рис. 1

Для заданного значения показателя «Прибыль на единицу продукции» подобрать значения показателей: «Цена единицы продукции»; «Постоянные расходы»; «Объем выпуска».

1.  Открыть рабочую книгу MATSTAT.xls.

2.  Выбрать лист РАСЧЕТЫ.

3.  Ввести исходные данные:

4.  Команда Сервис, Подбор параметра. Установить в ячейке В12 значение 10,25, изменяемая ячейка — В1. Нажать кнопку ОК.

В результате подбора в ячейке В1 появляется значение — 137,48 р. Нажать кнопку Отмена, если значение не должно сохраняться.

5.  Повторить п. 4 для подбора других параметров при том же значении функции.

6.  Сохранить рабочую книгу  MATSTAT.xls.

На начало ...

ВНИМАНИЕ. После завершения работы проверить наличие файлов:

Модуль "Математические и статистические методы анализа данных в MS Excel"

Поиск решения

Оптимальная производственная программа (прямая задача линейного программирования)	Транспортная задача
Анализ ресурсов (обратная задача линейного программирования )

Общая формулировка основной задачи линейного программирования (ОЗЛП): найти наибольшее значение линейной функции при выполнении определенных условий (ограничений).  Эта задача называется прямой задачей ЛП:

 

Целевая функция прямой задачи ЛП стремится к максимуму, позволяет получить оптимальный план (x), при котором целевая функция максимальна при соблюдении ограничений. Если все ограничения являются уравнениями, а на все переменные наложены условия не отрицательности значений, ОЗЛП называется канонической задачей линейного программирования (КЗЛП).

Для ОЗЛП всегда существует двойственная задача ЛП, для которой выполняются следующие условия:

§  целевая функция двойственной задачи стремится к минимуму;

§  для всех ограничений прямой задачи вводятся неотрицательные переменные y_i, i=1, n, которые являются искомыми для двойственной задачи;

§ ограничениями двойственной задачи являются неравенства типа >=;

§  матрица А={a_ij} используется в обычном представлении;

§ коэффициенты целевой функции прямой задачи с_j становятся свободными членами для ограничений двойственной задачи.

Модель двойственной задачи ЛП:

 

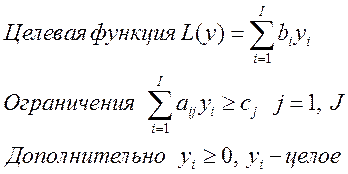
Целевая функция двойственной задачи стремиться к минимуму, позволяет получить оптимальную систему условных оценок ограничений (y) для прямой задачи. Значение переменной y_i в оптимальном плане двойственной задачи показывает, на сколько увеличивается оптимальное значение целевой функции прямой задачи при увеличении соответствующего ограничения (b_i ) на единицу.