Модуль "Математические и статистические методы анализа данных в MS Excel", страница 11

Функция БС вычисляет "будущую" стоимость вклада на основе его начальной стоимости и серии постоянных по величине периодических платежей, осуществляемых с заданной периодичностью в течение определенного срока. Процентная ставка фиксирована на весь срок платежей.

Синтаксис функции:    =БС(ставка; кпер; плт; пс; тип)

Процентная ставка и общее количество учетных периодов пересчитываются с учетом периодичности капитализации,  коэффициенты пересчета:

Периодичность дополнительных платежей соотносится с периодом капитализации процентов.

Сумма накопления на счете в конце разных учетных периодов изменяется неравномерно.

Пример.

На депозитном счете размещена  сумма 1000 р. сроком на 3 года под 10% годовых. Период капитализации - полугодие, дополнительный платеж составляет 300 р. и делается каждые полгода.
Формула расчета будущей стоимости: =БС(10%/2; 3*2; -300; -1000; 0). Сумма накопления - 338067 р.

Пример.

На депозитном счете размещена сумма 1000 р. сроком на 3 года под 10% без дополнительных периодических платежей. Период капитализации - год. Будущая стоимость вклада - 1331 р., формула расчета:  =БС(10%;3;0;-1000;0).

Пример.

На депозитном счета размещена  сумма 1000 р. сроком на 3 года под 10% годовых.  Период капитализации - год, дополнительный платеж в конце каждого полугодия - 300р.

Поскольку период капитализации больше периода платежей, суммы платежей накапливаются и учитываются в период капитализации. 
Формула расчета будущей стоимости: =БС(10%; 3;  -300*2;  -1000; 0).

Сумма накопления — 331700р.

Ниже приведены примеры, которые следует выполнять в рабочей книге FINEC.xls на листе КЭШ ФЛО. Исходные данные целесообразно хранить в отдельных ячейках.

Задание 32.

Период капитализации совпадает с периодом платежей -  раз в год.
а депозитном счете размещена сумма 1000 р. под 10% годовых. Периодические платежи для вариантов отличаются суммой (рис.1-3), но выполняются в конце учетного периода:

Вычислить суммы накопления для различных  вариантов платежей.

Задание 33.

а депозитном счете размещена сумма 1000 р. под 10% годовых. Периодических платежей нет. Вычислить накопленную сумму, если период капитализации: год,  полугодие,  квартал,  месяц.

1. Подготовить исходные данные о периодичности капитализации в виде:

  поле со списком для выбора периода капитализации - команда Данные, Проверка, тип данных - СПИСОК,
источник: ГОД; ПОЛУГОДИЕ; КВАРТАЛ; МЕСЯЦ

  коэффициент пересчета определяется автоматически (по формуле) - для периода ГОД коэффициент равен 1, для периода ПОЛУГОДИЕ - 2, КВАРТАЛ - 4, МЕСЯЦ - 12

2.  Использовать в формуле расчета накопленной суммы коэффициента пересчета.

Пример

На счете размещена сумма 1000 р. под 10% годовых сроком на 4 года.Имеют место дополнительные ежеквартальные вложения в конце квартала в сумме 50 р., капитализация на счете - раз в полгода.

  Построить таблицу, содержащую для каждого периода (полугодия) сумму накопления на счете.

  Определить прирост суммы накоплений по периодам.

  Построить график зависимости и тренд прироста суммы накоплений от времени (лет).

  Подобрать уравнение линии тренда.

Настоящая стоимость (ПС)

Функция ПС вычисляет "настоящую" стоимость вклада (pv), которая эквивалентна будущей стоимости вклада с учетом серии постоянных по величине периодических платежей, осуществляемых с заданной периодичностью в течение определенного срока. Процентная ставка фиксирована на весь срок платежей.

Синтаксис функции:  = ПС(ставка; кпер; плт; бс; тип)

Пример 35

Определить настоящую стоимость вклада сроком на 4 года под 10% годовых, если при платеже в конце каждого года 200 р. будет накоплена сумма 2392,30 р. Капитализация - раз в год.

Пример 36

Сколько нужно положить на счет под 10% годовых, чтобы при ежеквартальном платеже 50 р. накопить через 2 года сумму  1000 р. Капитализация - раз в год.

Пример 37

На какую сумму можно оформить кредит, выдаваемый на 4 года под 19% годовых с обязательством ежегодной выплаты процентов и погашения суммы долга не менее 1000 р. Капитализация - раз в год.

Функции ЭФФЕКТ и НОМИНАЛ

Ставка называется номинальной если период капитализации — год.
Эффективная ставка — ставка с учетом периодичности платежей и капитализации, пересчитанная на годовую периодичность. Номинальная ставка меньше эффективной ставки, если периодичность больше чем 1 раз в год.

Функции ЭФФЕКТ и НОМИНАЛ связаны соотношением:

 

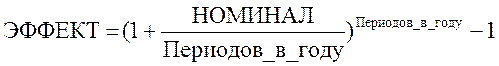
Функция ЭФФЕКТ возвращает эффективную ставку процентов, если заданы номинальная годовая процентная ставка и периодичность капитализации или платежей. 

Функция НОМИНАЛ возвращает номинальную ставку процентов, если известна известна эффективная ставка процентов.

Например номинальная ставка - 10%.
Эффективные ставки процентов для периодов капитализации:

Периодичность	Число периодов в году	ЭФФЕКТ
год	1	10,00%
полугодие	2	10,25%
квартал	4	10,38%
месяц	12	10,47%

Эффективной ставке 10% соответствуют номинальные ставки: