Модуль "Математические и статистические методы анализа данных в MS Excel", страница 13

На счете размещена сумма 10000 р. сроком на 5 лет под 10% годовых. Сумма накопления составит 18000 р. Определить по периодам:

   суммы выплат,

   сумму на счете,

   структуру начисления процентов и увеличения суммы накопления.

Изобразить графически полученные соотношения.

Накопительный процентный (ОБЩПЛАТ) и основной (ОБЩДОХОД) платеж

Функция ОБЩПЛАТ вычисляетсумму процентов за интервал учетных периодов (начальный – конечный), является итогом для смежных учетных периодов, вычисленных с помощью функции ПРПЛТ.

Синтаксис функции:  = ОБЩПЛАТ(ставка; кпер; пс; начальный_период; конечный_период; тип)

Функция ОБЩДОХОД вычисляет сумму накопления (выплаты долга) за интервал учетных периодов(начальный – конечный), является итогом для смежных учетных периодов, вычисленныхс помощью функции ОСПЛТ.

Синтаксис функции:  = ОБЩДОХОД(ставка; кпер; пс; начальный_период; конечный_период; тип)

Эти функции имеют специфику вычисления:

1.  Для погашения кредита (ссуды) величины ОБЩПЛАТ и ОБЩДОХОД — отрицательные.

2.  Для расчетов по депозитному счету в функциях ОБЩПЛАТ и ОБЩДОХОД значение параметра начальной суммы вклада указывается как положительное число. Вычисляемое значение ОБЩДОХОД показывает накопленную сумму дополнительных взносов и процентов за интервал времени.

К концу любого n-го учетного периода (N — общее число периодов договора, начальный период равен 1) выполняется соотношение:

ОБЩПЛАТ_n + ОБЩДОХОД_n= n* ПЛТ  n = 1 N.

Эта сумма показывает накопленную сумму выплат в интервале от начала договора до текущего учетного периода.

Пример 45.

Взят кредит 10000 р. сроком на 5 лет под 20% годовых. Определить за каждый интервал: первый год, первые два года, первые три года, за весь срок (четыре года):

  суммы выплат,

  изменение суммы долга,

  сумму выплат процентов за пользование кредитом и в счет погашения долга.

Изобразить графически полученные соотношения.

Пример 46.

На счете размещена сумма 10000 р. сроком на 5 лет под 10% годовых. Сумма накопления составит 18000 р. Определить за каждый интервал: первый год, первые два года, первые три года, за весь срок (четыре года):

  суммы выплат,

  изменение суммы вклада,

  сумму процентов и накоплений.

Изобразить графически полученные соотношения.

Непериодические или нефиксированные платежи, переменная ставка процентов

Если платежи непериодические, а величина платежа — переменная  (рис.7), денежный поток представляется в виде совокупности потоков по отдельным платежам.

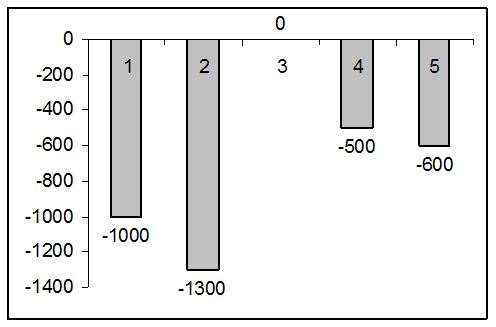
Рисунок 7

Например, вычислить сумму накопления на депозитном счете за 4 года, если начальная сумма составляет 1000 р. с последующим вложением средств по схеме:

Период	Сумма в начале периода	Сумма вложений в конце периода	Сумма накоплений в конце периода	Ставка процентов за период	Формула расчета
1	1000,00	1000	2100,00	10%	=БС(10%;1;-1000;-1000;0)
2	2100,00	1300	3589,00	9%	=БС(9%;1;-1300;-2100;0)
3	3589,00	0	3804,34	6%	=БС(6%;1;0;-3589;0)
4	3804,34	500	4494,56	5%	=БС(5%;1;-500;-3804,34;0)

Пример 47.

Вычислить сумму накопления на депозитном счете за 6 лет, если начальная сумма составляет 3000 р. с последующим вложением средств по схеме: 

Период	Сумма взноса	Ставка процентов
Первоначальная сумм	-3000
1	-500	10%
2	0	10%
3	-500	9%
4	0	9%
5	-500	8%
6	0	8%

Вычислить эквивалентную постоянную ставку процентов для средней суммы дополнительного периодического платежа.

Переменная ставка процентов

Функция БЗРАСПИС

Функция БЗРАСПИС обеспечивает вычисление накопленной суммы для начальной суммы без периодических платежей когда процентная ставка изменяется во времени действия договора. Синтаксис функции:

  =БЗРАСПИС(пс;{массив_ставок_процентов})

Пример 48.

На депозитном счете размещена сумма 1000 р. сроком  на 4 года,  процентная ставка изменяется по годам:

Для решения задачи требуется ввести процентные ставки в ячейки таблицы, например А12:D12 (или задать их в виде массива констант в фигурных скобках при вводе формулы). Значение начальной суммы указать в виде положительного значения.

Формула расчета: =БЗРАСПИС(1000; A12:D12). Результат — 1 347,08р.

С помощью информационной технологии подбора параметра можно определить эквивалентную постоянную ставку процента (в данном примере — 7,73%).

Инвестиционные проекты

Инвестиционный проект — целенаправленная деятельность, связанная с финансовыми затратами. Как правило, вложения в инвестиционные проекты обеспечивают доход.  Примеры инвестиционных проектов:

- расширение масштабов производства («расширяющаяся отдача от масштаба»);

- освоение новых видов деятельности;

- замещение производственных мощностей;

- увеличение ресурсного потенциала и др.

Классификация инвестиционных проектов осуществляется по различным признакам, например:

- тип инвестиционного проекта (долгосрочные - свыше 10 лет, среднесрочные  - 3-10 лет и краткосрочные проекты - до 3 лет);

- сумма инвестиций (круномасштабные - около 1 млн. долл., традиционные  - до 100000 р., мелкие инвестиционные проекты - несколько тысяч руб.);