Модуль "Математические и статистические методы анализа данных в MS Excel", страница 6

Рис. 4

В отчете показано отличие полученного оптимального результата от предшествующего, статус для строк ограничений:

  Связанное - достигнут предел ограничения, разница равна 0;

  Несвязанное - не достигнут предел ограничения, разница между пределом и используемым значением больше 0.

Не связанное значение свидетельствует о том, что изменение ограничений для ресурсов приведет к изменению значения целевой функции.

13. Сохранить рабочую книгу MATSTAT.xls.

Пример 23. Решение двойственной задачи линейного программирования

Схема подготовки исходных данных для решения двойственной задачи — рис. 5.

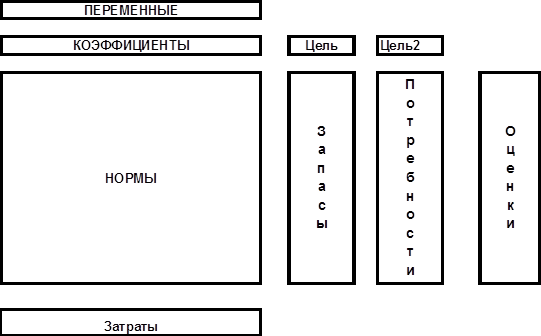
Рис. 5

1.  Открыть рабочую книгуMATSTAT.xls, лист —  ПОИСК РЕШЕНИЯ1.

2. Создать новые блоки:

Оценки — вектор-столбец, размер блока определяется числом ограничений прямой задачи;

Затраты — вектор-строка, размер блока определяется числом переменных прямой задачи;

Цель2 — блок в одну ячейку.

2. Задать формулы для блока Цель2:

  =СУММПРОИЗВ(ЗАПАСЫ;ОЦЕНКИ)

3. Для первой ячейки блока ЗАТРАТЫ ввести формулу:

  =СУММПРОИЗВ(A5:A7;ОЦЕНКИ)

 - сумма произведений первого столбца блока НОРМЫ (A5:A7) и блока ячеек ОЦЕНКИ.
Формулу следует размножить по ячейкам блока ЗАТРАТЫ.

4. Построить модель двойственной задачи — команда Сервис, Поиск решения:

Целевая ячейка — блок Цель2, стремится кминимальному значению, Изменяя ячейки — блок ОЦЕНКИ

Ограничения: 

    ЗАТРАТЫ >=КОЭФФИЦИЕНТЫ

  ОЦЕНКИ >=0

  ОЦЕНКИ = целые

5.В окне ПОИСК РЕШЕНИЯ нажать кнопку Параметры, переход в окно ПАРАМЕТРЫ ПОИСКА РЕШЕНИЯ. Нажать кнопку Сохранить модель.  Нажать кнопку ОК для возврата в окно ПОИСК РЕШЕНИЯ. Нажать кнопку Закрыть для выхода из окна ПОИСК РЕШЕНИЯ. Ознакомиться с видом модели задачи оптимизации (рис.6). 

Рис. 6

6. Выполнить команду Сервис, Поиск решения. Решить задачу — кнопка Выполнить, вывести отчет Результаты.

Отчет Результаты имеет следующий вид (рис. 7):

Целевая функция  (Min)
	Ячейка	Имя	Исходное значение	Результирующее значение
	$H$21	Цель2	0	1200
Изменяющиеся ячейки
	Ячейка	Имя	Исходное значение	Результирующее значение
	$J$36	Оценки	0	3
	$J$37	Оценки	0	0
	$J$38	Оценки	0	0
	$J$39	Оценки	0	0
	$J$40	Оценки	0	0
	$J$41	Оценки	0	0
	$J$42	Оценки	0	1
Ограничения
	Ячейка	Имя	Значение	Формула	Статус	Разница
	$A$45	-->	18	$A$45>=$A$23	Не связанное	3
	$B$45		27	$B$45>=$B$23	Не связанное	5
	$C$45		30	$C$45>=$C$23	Связанное	0
	$D$45		27	$D$45>=$D$23	Не связанное	17
	$J$36	Оценки	3	$J$36>=0	Не связанное	3
	$J$37	Оценки	0	$J$37>=0	Связанное	0
	$J$38	Оценки	0	$J$38>=0	Связанное	0
	$J$39	Оценки	0	$J$39>=0	Связанное	0
	$J$40	Оценки	0	$J$40>=0	Связанное	0
	$J$41	Оценки	0	$J$41>=0	Связанное	0
	$J$42	Оценки	1	$J$42>=0	Не связанное	1
	$J$36	Оценки	3	$J$36=integer	Связанное	0
	$J$37	Оценки	0	$J$37=integer	Связанное	0
	$J$38	Оценки	0	$J$38=integer	Связанное	0
	$J$39	Оценки	0	$J$39=integer	Связанное	0
	$J$40	Оценки	0	$J$40=integer	Связанное	0
	$J$41	Оценки	0	$J$41=integer	Связанное	0
	$J$42	Оценки	1	$J$42=integer	Связанное	0

Рис. 7

Прямая и двойственная задачи имеют одинаковое значение целевой функции; увеличение запасов ресурсов должно дать следующее увеличение целевой функции (табл. 4):

Таблица 4

Ресурсы	Запас начальный	Рост целевой функции при увеличении запаса ресурса  на единицу
1	200	3
2	200	0
3	50	0
4	800	0
5	700	0
6	100	0
7	600	1

7. Сохранить рабочую книгу MATSTAT.xls.

В начало ..

Транспортная задача

 «Транспортная задача» широко применяется для решения задач поиска оптимального плана «перевозок» — между пунктами производства и пунктами потребления.