Модуль "Математические и статистические методы анализа данных в MS Excel", страница 5

Схема расположения параметров модели

 

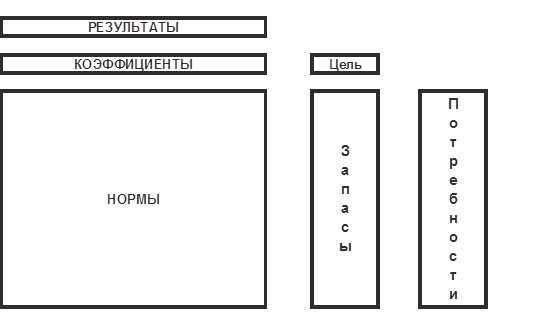
Рис. 1

Пример 22. Решение прямой задачи линейного программирования

Номенклатура продукции и доход от ее реализации приведен в табл. 2

Таблица 2

Номенклатура и характеристика ресурсов для изготовления продукции приведены в табл.3.

Таблица 3

Ресурс	Запас	Ед. изм.	Цена, руб.
1	200	Кг	150
2	120	Шт	100
3	40	Т	1250
4	760	Н-Час	25
5	480	Ст-час	4
6	40	Комп.	115
7	600	Руб.	1

Норма расхода ресурсов на выпуск единицы продукции показаны в табл. 4.

Таблица 4

Ресурсы	Изделия
	А	Б	В	Г
1	2	4	5	2
2	7	12	3	12
3	1	3	1	0
4	25	35	19	50
5	23	43	12	11
6	2	4	1	1
7	12	15	15	21

1.  Открыть рабочую книгуMATSTAT.xls.

2.  Вставить и переименовать лист —  ПОИСК РЕШЕНИЯ1.

3.  Расположить исходные данные согласно рис.1.

4.  Создать именованные блоки (см. табл.2).

5.  Сведения о цене ресурсов представить в виде отдельного столбца, для которого создать именованный блок — ЦЕНА.

6.  Ввести формулу для целевой функции:

  =СУММПРОИЗВ(РЕЗУЛЬТАТЫ; КОЭФФИЦИЕНТЫ)

7.  Ввести формулу для расчета потребности ресурса, например, для первого ресурса — сумма произведений первой строки блока НОРМА и ячеек блока РЕЗУЛЬТАТЫ:

  =СУММПРОИЗВ(РЕЗУЛЬТАТЫ;A25:D25),

A25:D25 - диапазон ячеек, соответствующий вектор-строке матрицы НОРМЫ для первого ресурса в блоке ПОТРЕБНОСТИ. Размножить формулу по ячейкам блока ПОТРЕБНОСТИ.

8.  Ввести формулу для вычисления суммарных затрат ресурсов на реализацию производственной программы — формула: 

    =СУММПРОИЗВ(ПОТРЕБНОСТИ; ЦЕНА)

9. Установить курсор в пустую ячейку вне исходных данных (для сохранения модели задачи).

10. Выполнить команду Сервис, Поиск решения. Ввести параметры модели нахождения оптимального решения (рис.2).

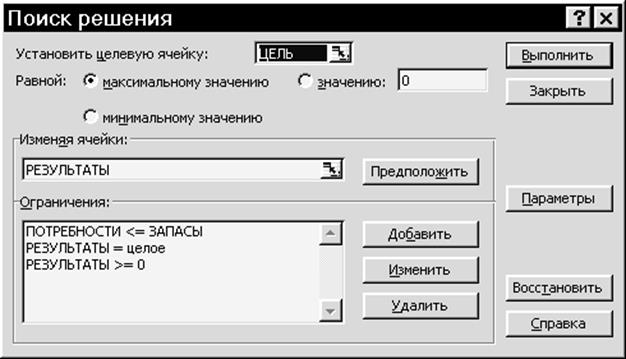
Рис. 2

11. В окне ПОИСК РЕШЕНИЯ нажать кнопку Параметры, переход в окно ПАРАМЕТРЫ ПОИСКА РЕШЕНИЯ.

Задать параметры:
Максимальное время - 1000 секунд,
Предельное число итераций - 10000,
Относительная погрешность - 0,001, 
Допустимое отклонение 5%,
Сходимость 0,0001.

Установить флажки:
Линейная модель, Автоматическое масштабирование, Показывать результаты итераций.

Указать:
Оценки - линейные, Разности - прямые, Метод поиска - Ньютона.

Нажать кнопку Сохранить модель (MS Excel автоматически определяет необходимое число ячеек для записи модели, исходя из общей размерности задачи).  Нажать кнопку ОК для возврата в окно ПОИСК РЕШЕНИЯ. Нажать кнопку Закрыть для выхода из окна ПОИСК РЕШЕНИЯ. Ознакомиться с видом модели задачи оптимизации (рис. 3). 

Рис. 3

12. Выполнить команду Сервис, Поиск решения. Решить задачу — кнопка Выполнить. Вывести отчет Результаты (рис. 4)ипроанализировать результаты решения.

Целевая функция (Max)
	Ячейка	Имя	Исходное значение	Результирующее значение
	$G$21	Цель	0	1200
Изменяющиеся ячейки
	Ячейка	Имя	Исходное значение	Результирующее значение
	$A$21	НОРМЫ	0	0
	$B$21		0	0
	$C$21		0	40
	$D$21		0	0
Ограничения
	Ячейка	Имя	Значение	Формула	Статус	Разница
	$H$36	Потребности	200	$H$36<=$F$36	Связанное	0
	$H$37	Потребности	120	$H$37<=$F$37	Не связанное	80
	$H$38	Потребности	40	$H$38<=$F$38	Не связанное	10
	$H$39	Потребности	760	$H$39<=$F$39	Не связанное	40
	$H$40	Потребности	480	$H$40<=$F$40	Не связанное	220
	$H$41	Потребности	40	$H$41<=$F$41	Не связанное	60
	$H$42	Потребности	600	$H$42<=$F$42	Связанное	0
	$A$21		0	$A$21>=0	Связанное	0
	$B$21		0	$B$21>=0	Связанное	0
	$C$21		40	$C$21>=0	Не связанное	40
	$D$21		0	$D$21>=0	Связанное	0
	$A$21		0	$A$21=целое	Связанное	0
	$B$21		0	$B$21=целое	Связанное	0
	$C$21		40	$C$21=целое	Связанное	0
	$D$21		0	$D$21=целое	Связанное	0