Основные понятия векторной алгебры. Проекция вектора на ось. Координаты вектора. Скалярное произведение векторов, страница 8

        Уравнения прямой, записанные в таком виде, называются параметрическими уравнениями прямой.

Доказательство.

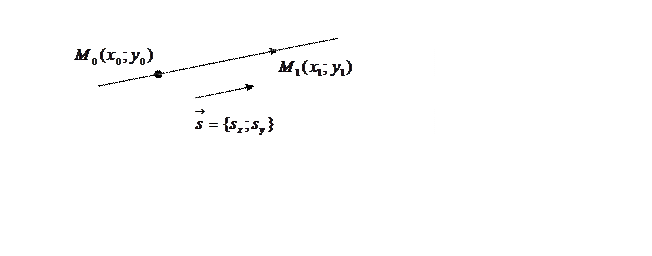
Рис. 36.

           Пусть прямая проходит через точку  иколлинеарнавектору 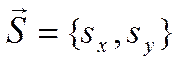.Возьмем на прямой произвольную точку  , отличную  от точки . Так как точка   лежит на прямой, то вектор  коллинеарен вектору 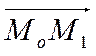 . Значит существует такое единственное число , что 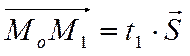  есть верное векторное равенство.  Так как

,

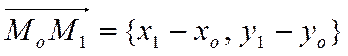то в координатах равенство запишется в виде

.

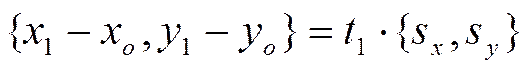Так как равные векторы имеют равные координаты, то

,

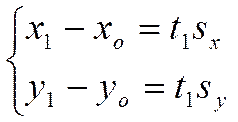Или

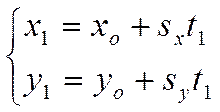
есть система верных числовых равенств. Следовательно, тройка чисел 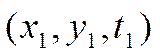  является решением системы уравнений

.

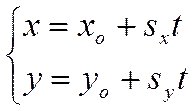Непосредственной подстановкой в эту систему тройки чисел нетрудно убедиться, что эта тройка чисел является решением системы уравнений. Таким образом, какова бы ни была точка  на рассматриваемой кривой, существует единственное для выбранной точки число  такое, что тройка чисел  является решением рассмотренной выше системы уравнений.

        Докажем теперь, что если тройка чисел  есть решение системы уравнений

,

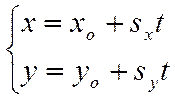то точка   лежит на прямой. Доказательство проведем от противного.  Допустим, что точка  не лежит на прямой. Тогда вектор 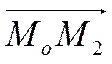 (Рис. 37) не

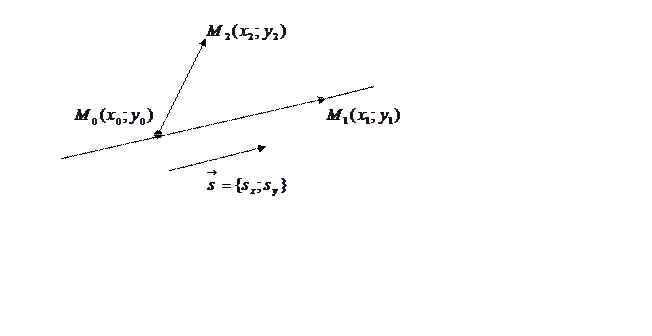
Рис. 37.

коллинеарен  прямой и значит не существует такого числа , что выполняется равенство

.

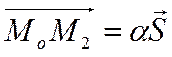Или в координатах

.

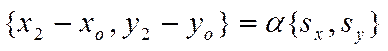А это означает, что ни при каком   не является верной система числовых равенств

.

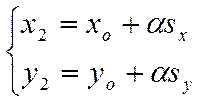Но это утверждение противоречит тому, что тройка чисел  является решением системы уравнений

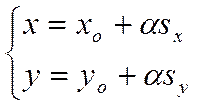
и, следовательно, является верной система числовых равенств

.

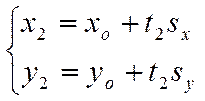            Так как для любой прямой на плоскости можно указать точку, через которую она проходит, и коллинеарный ей вектор, то уравнение любой прямой на плоскости можно записать в виде

.

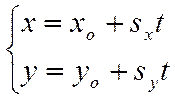Справедливо и обратное утверждение о том, что система уравнений

,

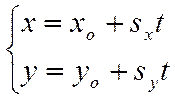где хотя бы одно из чисел   и   отлично от нуля, является системой уравнений для некоторой прямой на плоскости. Действительно, как показано выше, такой прямой будет прямая, проходящая через точку и коллинеарная вектору .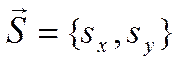

           Теперь рассмотрим так называемое каноническое уравнение прямой на плоскости. Утверждение о каноническом уравнении прямой сформулируем в виде теоремы.

Теорема.

       Если прямая на плоскости проходит через точку 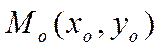 и коллинеарна вектору  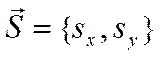, то уравнение этой прямо можно записать в виде (при условии, что  и  )

.

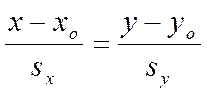Уравнение прямой, записанное в таком виде, называется каноническим уравнением прямой на плоскости.

Доказательство.

     Пусть   - произвольная точка на прямой (Рис. 38).. Тогда вектор   коллинеарен вектору    и значит

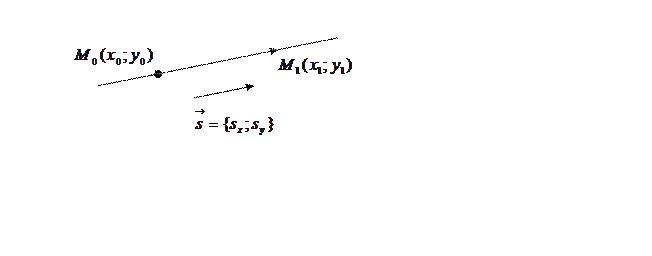
Рис. 38.

существует  такое число , что  справедливо векторное равенство

.

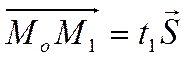Из верного векторного равенства следует система верных равенств для координат векторов

.

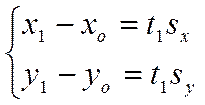Или, так как 

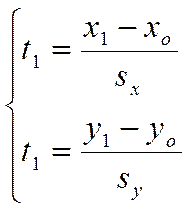
есть верные числовые равенства. Но тогда

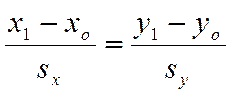
является верным числовым равенством и значит пара чисел есть решение уравнения

.

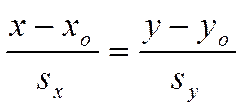Докажем теперь, что если пара чисел 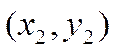 есть решение этого уравнения, то точка   лежит на этой прямой. Доказательство проведем от противного. Допустим, что точка   не лежит на этой прямой (Рис. 37). Тогда вектор 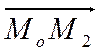  не коллинеарен вектору  и значит не при каком числе  не является верным векторное равенство

.

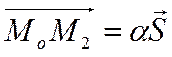Или, переходя к координатам, получаем, что система числовых равенств

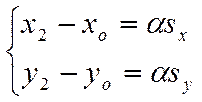
не является верной ни при каком . Но тогда не при каком  не является верной система равенств

  .

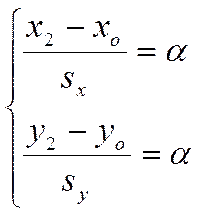Отсюда следует, что не является верным равенство

.

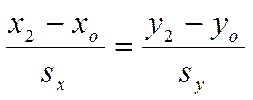Но это противоречит тому, что пара чисел   является решением уравнения

.

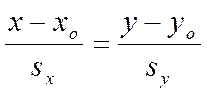Следовательно, точка  лежит на прямой.

         Итак доказано, что уравнение

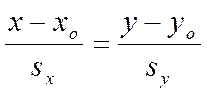
является уравнением прямо, проходящей через точк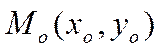у  и коллинеарной вектору  .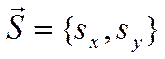

Рассмотрим пример.

Пример.  

     Записать параметрические и каноническое уравнения прямой на плоскости, проходящей через точку  и коллинеарной вектору .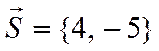

Решение.

    Параметрические уравнения прямой имеют вид

,

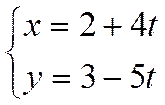каноническое уравнение прямой запишется в виде

.

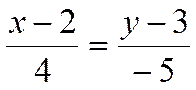         Теперь рассмотрим как можно перейти от уравнения прямой одного вида к уравнению прямой другого вида. Прежде всего заметим, что если    есть вектор нормали к прямой, то в качестве направляющего вектора прямой  можно взять либо вектор , либо вектор . В самом деле, в этом случае  и значит вектор , будучи перпендикулярным вектору нормали, будет коллинеарен прямой. Переход от одного вида уравнения прямой к другому рассмотрим на примерах.

Пример. 

       Дано уравнение прямой

.

Записать каноническое и параметрические уравнения прямой.

Решение.

       Нормаль к прямой равна

.

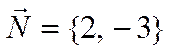Поэтому в качестве направляющего вектора можно взять

.

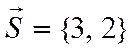Одним из решений уравнения является пара . Поэтому точка   лежит на прямой. Следовательно, каноническое уравнение прямой имеет вид

.

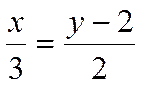Параметрическими уравнениями прямой будут

.

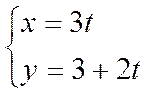Пример.  

         Дано каноническое уравнение прямой

.

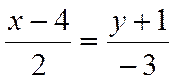Записать общее уравнение прямой.

Решение.

Избавляясь от знаменателей путем умножения обеих частей уравнения на , получим

.

Или

.

§3. Взаимное расположение прямых на плоскости

          Из элементарной геометрии известно, что две прямые могут совпадать, быть параллельными или пересекаться в одной точке. Допустим, что уравнения прямых   и   имеют вид

,

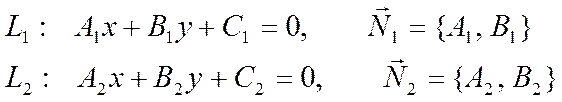где   и 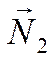  - векторы нормалей прямых. Тогда, если прямые совпадают или параллельны, то их нормали коллинеарны и значит существует число   такое, что выполняется равенство

.

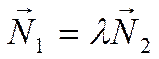При этом, из элементарной геометрии известно, что если хотя бы одна точка, лежащая на одной из прямых, лежит и на другой прямой, то прямые совпадают. Если же ни одна точка, лежащая на одной из прямых, не лежит на другой прямой, то прямые параллельны. Рассмотрим примеры.

Пример.