Основные понятия векторной алгебры. Проекция вектора на ось. Координаты вектора. Скалярное произведение векторов, страница 11

не является верным числовым равенством. Но это противоречит сделанному предположению о том, что тройка чисел  есть решение уравнения

,

и значит равенство

есть верное числовое равенство. Следовательно, предположение о том, что точка   не лежит на плоскости не верно. Следовательно, точка  лежит на плоскости. Теорема доказана.

Пример.

       Записать уравнение плоскости, проходящей через точку   и перпендикулярной вектору  .

Решение.

        Как показано выше, уравнение имеет вид

или

.

     Если в уравнении

раскрыть скобки, то получим уравнение вида

.

Обозначим

.

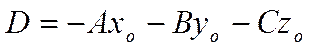Тогда уравнение примет вид

.

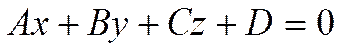Таким образом, уравнение любой плоскости можно записать в виде

.

При этом вектор нормали к плоскости равен 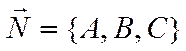. Уравнение плоскости, записанное в таком виде, называется общим уравнением плоскости. Можно показать, что уравнение вида

,

где хотя бы одно из чисел   отлично от нуля, есть уравнение какой-то плоскости.

        Как известно из элементарной геометрии, через три точки, не лежащие на одной прямой, можно провести плоскость и при том только одну. В связи с этим в общем виде рассмотрим следующую задачу. Записать уравнение плоскости, проходящей через три точки

,

не лежащие на одной прямой.

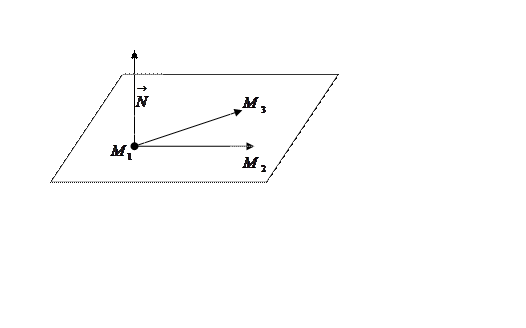
Рис. 46.

Векторы 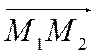  и 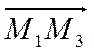  лежат в плоскости и не коллинеарны так как точки  не лежат на одной прямой. Тогда вектор 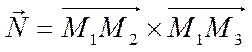 , будучи перпендикулярным векторам 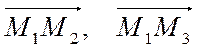, будет перпендикулярен плоскости . Следовательно, вектор 

 можно взять в качестве нормали к плоскости. Тогда поставленная задача сводится к решению рассмотренной выше задачи: записать уравнение плоскости, проходящей через точку 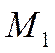 и перпендикулярной вектору . Уравнение этой плоскости можно записать в виде

.

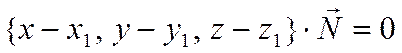Так как , то левая часть уравнения принимает вид смешанного произведения векторов

.

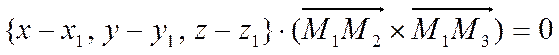Учитывая, что

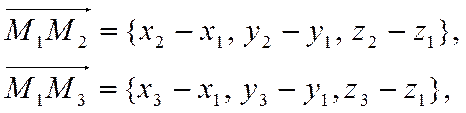
и что смешанное произведение можно записать в виде определителя,  получим искомое уравнение плоскости в виде

.

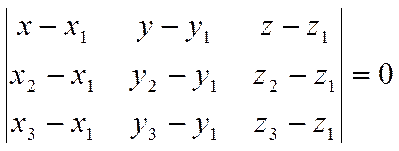Если разложить этот определитель по строке или столбцу, то окончательно уравнение примет вид общего уравнения плоскости.

Пример.

        Записать уравнение плоскости, проходящей через точки .

Решение.

         Выше получено, что уравнение имеет вид

.

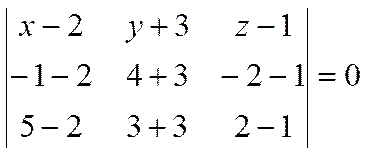Или

.

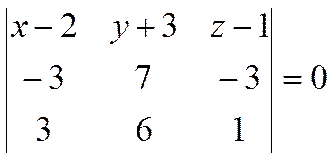Разлагая определитель, например по первой строке, получим искомое уравнение плоскости

.

§ 2. Взаимное расположение плоскостей в пространстве

        Две плоскости могут совпадать, быть параллельными или пересекаться по прямой. Ниже рассматривается вопрос о том, как по уравнениям плоскостей определить их взаимное расположение.

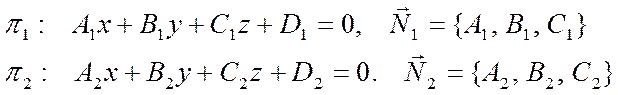
        Пусть две плоскости  и   заданы своими уравнениями

 и 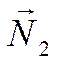  - нормали плоскостей   и  , соответственно.

          Из элементарной геометрии следует, что плоскости совпадают или параллельны тогда и только тогда, когда их нормали коллинеарны, то есть существует число    такое, что справедливо равенство

.

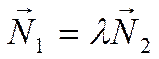Если плоскости совпадают, то все точки у них общие. Поэтому любое решение уравнения одной плоскости будет также решением уравнения другой плоскости. Если это не выполняется, то плоскости параллельны.

Пример.  

        Даны две плоскости, заданные уравнениями

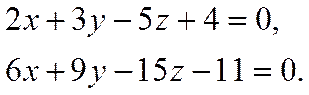
Определить взаимное расположение плоскостей.

Решение.

        Векторы нормалей равны

.

Так как

,

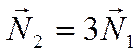то нормали коллинеарны и значит плоскости либо совпадают, либо параллельны. Легко проверить, что тройка чисел 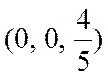 является решением первого уравнения и не является решением второго. Следовательно, плоскости параллельны.

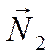         Если векторы   и   не коллинеарны, то есть условие 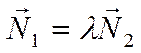  не выполняется ни при каком  , то плоскости пересекаются по прямой. В этом случае можно поставить вопрос об угле, под которым они пересекаются. Пересекающиеся плоскости образуют двугранные углы, мерой которых являются мера соответствующего линейного угла. Так же как и в случае пересекающихся прямых на плоскости, пересекающиеся плоскости (если они не перпендикулярны) образуют острый и тупой двугранные углы, который в сумме составляют . Из элементарной геометрии следует, что линейные углы равны углам между векторами нормалей к плоскостям. При этом, если угол между нормалями острый, то этот угол равен острому двугранному углу (и соответствующему ему линейному углу), а если тупой, то он равен тупому двугранному углу, образованному плоскостями. Как известно, косинус угла между нормалями можно найти по формуле

.

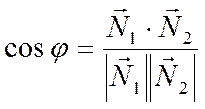Если получаем, что , то угол   - острый угол, равный острому двугранному углу между плоскостями. Если , то  равен тупому двугранному углу между плоскостями.

          Как и в случае пересекающихся прямых на плоскости, если поставить задачей найти острый угол между плоскостями,  то можно получить следующее выражение для острого угла

.

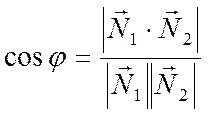Пример.  

      Даны плоскости, заданные уравнениями

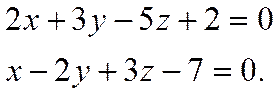
Найти острый угол между плоскостями.

Решение.

         Векторы нормалей равны

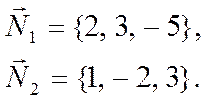
Следовательно, косинус острого угла равен

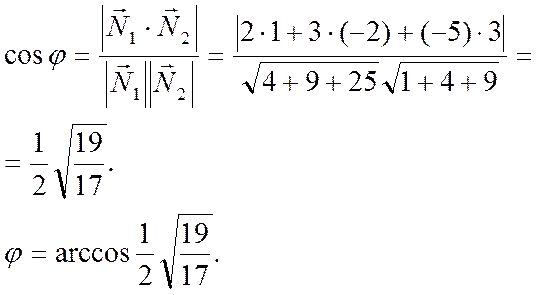
          Наконец, рассмотрим условие перпендикулярности плоскостей. Как следует из элементарной геометрии, две плоскости будут взаимно перпендикулярными тогда и только тогда, когда взаимно перпендикулярны их нормали, то есть их скалярное произведение равно нулю

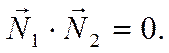
Пример.

          Доказать, что плоскости

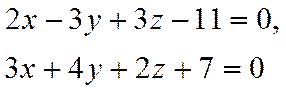
взаимно перпендикулярны.

Решение.

       Векторы нормалей равны

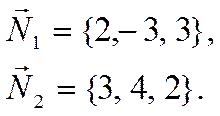
Находим скалярное произведение

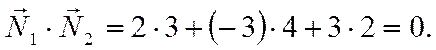
Следовательно, нормали перпендикулярны, а значит и плоскости взаимно перпендикулярны. 

Глава 4. Прямая в пространстве

§1. Общие уравнения прямой в пространстве