При сложении векторов их координаты складываются а при умножении вектора на число его координаты умножаются на это число. Записываются эти утверждения в виде
![]() ,
,
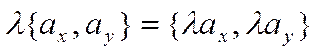 .
.
Доказательство.
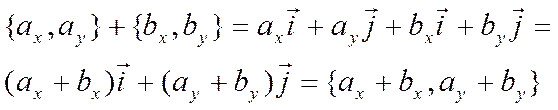 ,
,
![]() .
.
Далее установим как связаны координаты вектора с координатами его концов.
Теорема.
Пусть 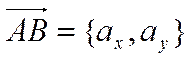 , причем начало вектора точка
, причем начало вектора точка ![]() имеет координаты
имеет координаты ![]() , а конец вектора есть точка
, а конец вектора есть точка ![]() . Тогда координаты вектора связаны с
координатами его концов следующими соотношениями
. Тогда координаты вектора связаны с
координатами его концов следующими соотношениями
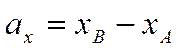 ,
,
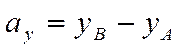 .
.
Доказательство.
Пусть 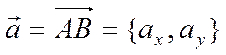 и пусть вектор-проекция вектора
и пусть вектор-проекция вектора ![]() на ось
на ось ![]()
![]() сонаправлен с осью
сонаправлен с осью ![]() (см. рис. 22). Тогда
(см. рис. 22). Тогда
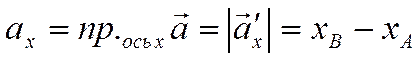 ,
,
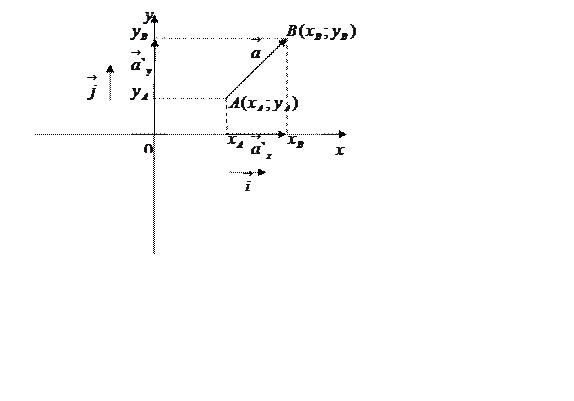 так как длина отрезка на
числовой оси
так как длина отрезка на
числовой оси ![]() равна координате правого конца минус
координата левого конца. Если вектор
равна координате правого конца минус
координата левого конца. Если вектор ![]()
![]()
Рис. 22.
![]() противонаправлен
оси
противонаправлен
оси ![]() (как на Рис. 23), то
(как на Рис. 23), то
 .
.
 Рис. 23.
Рис. 23.
Если 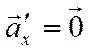 ,
то в этом случае
,
то в этом случае ![]() и тогда получаем
и тогда получаем
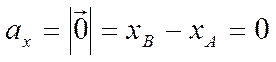 .
.
Таким образом, при любом
расположении вектора ![]() относительно осей координат
его координата
относительно осей координат
его координата ![]() равна
равна
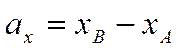 .
.
Аналогично доказывается, что
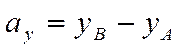 .
.
Пример.
Даны координаты концов вектора 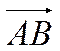 :
: ![]() .
Найти координаты вектора
.
Найти координаты вектора 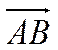 .
.
Решение.
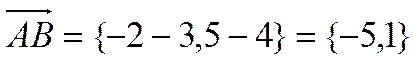 .
.
В следующей теореме приводится выражение длины вектора через его координаты.
Теорема 15.
Пусть 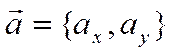 .Тогда
.Тогда
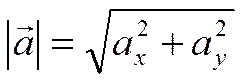 .
.
Доказательство.
Пусть 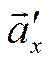 и
и 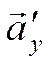 -
вектор-проекции вектора
-
вектор-проекции вектора ![]() на оси
на оси ![]() и
и ![]() ,
соответственно. Тогда, как показано при доказательстве теоремы 9, имеет место
равенство
,
соответственно. Тогда, как показано при доказательстве теоремы 9, имеет место
равенство
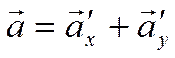 .
.
При этом, векторы ![]() и
и ![]() взаимно
перпендикулярны. При сложении этих векторов по правилу треугольника получаем
прямоугольный треугольник (см. Рис. 24).
взаимно
перпендикулярны. При сложении этих векторов по правилу треугольника получаем
прямоугольный треугольник (см. Рис. 24).

Рис. 24.
По теореме Пифагора имеем
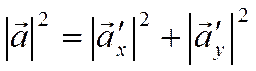 .
.
Но
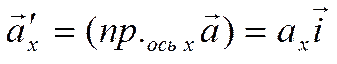 ,
,
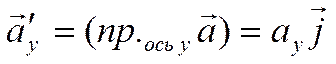 .
.
Следовательно
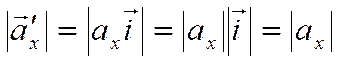 ,
,
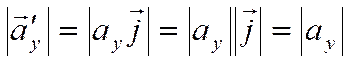 .
.
Отсюда
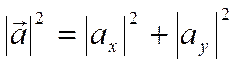 .
.
Или
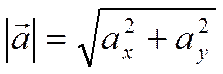 .
.
Пример.
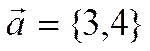 .Найти
.Найти ![]() .
.
Решение.
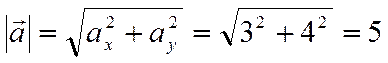 .
.
Введем понятие направляющих косинусов вектора .
Определение.
Пусть вектор  составляет с осью
составляет с осью ![]() угол
угол ![]() ,
а с осью
,
а с осью ![]() угол
угол ![]() (см.
Рис. 25).
(см.
Рис. 25).
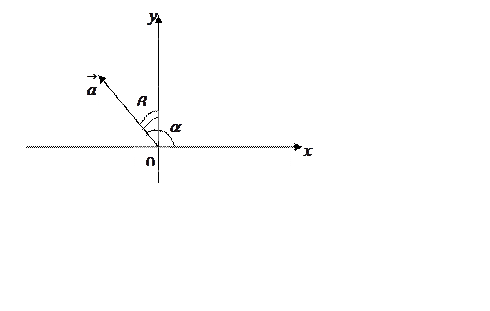
Рис. 25.
Тогда
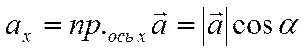 ,
,
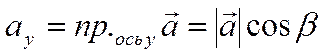 .
.
Следовательно,
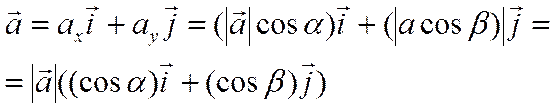
Так как для любого вектора ![]() имеет место равенство
имеет место равенство
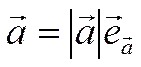 ,
,
Где ![]() -
орт вектора
-
орт вектора ![]() , то есть вектор единичной длины,
сонаправленный с вектором
, то есть вектор единичной длины,
сонаправленный с вектором ![]() , то
, то
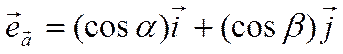 .
.
Вектор ![]() определяет
направление вектора
определяет
направление вектора ![]() . Его координаты
. Его координаты ![]() и
и  называются
направляющими косинусами вектора
называются
направляющими косинусами вектора ![]() . Направляющие
косинусы вектора можно выразить через его координаты по формулам
. Направляющие
косинусы вектора можно выразить через его координаты по формулам
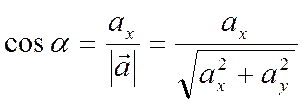 ,
,
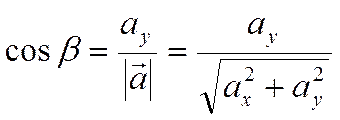 .
.
Имеет место соотношение
![]()
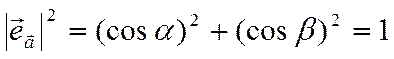 .
.
До настоящего момента в этом параграфе считалось, что все векторы располагаются в одной и той же плоскости. Теперь сделаем обобщение для векторов в пространстве.
Будем считать, что в
пространстве задана Декартова система координат с осями ![]() ,
,
![]() и
и ![]() .
.
Орты осей ![]() ,
,
![]() и
и ![]() будем
обозначать символами
будем
обозначать символами ![]() ,
, ![]() и
и
![]() , соответственно (Рис. 26).
, соответственно (Рис. 26).
Можно показать, что все понятия и формулы, которые были получены для векторов на плоскости, обобщаются для
 Рис.
26.
Рис.
26.
векторов в пространстве. Тройка
векторов  называется ортонормированным базисом
в пространстве.
называется ортонормированным базисом
в пространстве.
Пусть ![]() ,
, 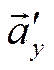 и
и
![]() - вектор-проекции вектора
- вектор-проекции вектора ![]() на оси
на оси ![]() ,
,
![]() и
и ![]() ,
соответственно. Тогда
,
соответственно. Тогда
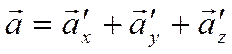 .
.
В свою очередь
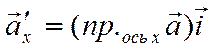 ,
,
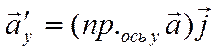 ,
,
 .
.
Если обозначить
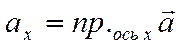 ,
,
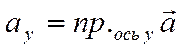 ,
,
 ,
,
То получаем равенство
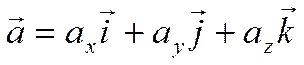 .
.
Коэффициенты перед базисными
векторами ![]() ,
, ![]() и
и ![]() называются координатами вектора
называются координатами вектора ![]() . Таким образом, для любого вектора
. Таким образом, для любого вектора ![]() в пространстве существует тройка
чисел
в пространстве существует тройка
чисел ![]() ,
, ![]() ,
,
![]() , называемых координатами вектора
, называемых координатами вектора ![]() таких, что для этого вектора
справедливо представление
таких, что для этого вектора
справедливо представление
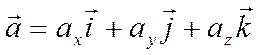 .
.
Вектор ![]() в
этом случае также обозначают в виде
в
этом случае также обозначают в виде  . При этом,
координаты вектора равны проекциям этого вектора на координатные оси
. При этом,
координаты вектора равны проекциям этого вектора на координатные оси
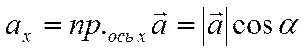 ,
,
 ,
,
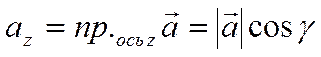 ,
,
где ![]() -
угол между вектором
-
угол между вектором ![]() и осью
и осью ![]() ,
, ![]() -
угол между вектором
-
угол между вектором ![]() и осью
и осью ![]() ,
, ![]() -
угол между вектором
-
угол между вектором ![]() и осью
и осью ![]() .
.
Длина вектора ![]() выражается через его координаты по
формуле
выражается через его координаты по
формуле
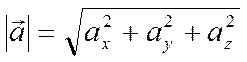 .
.
Справедливы утверждения
о том, что равные векторы имеют равные координаты, при сложении векторов их
координаты складываются, а при умножении вектора на число его координаты
умножаются на это число. ![]() ,
, ![]() и
и ![]() называются
направляющими косинусами вектора
называются
направляющими косинусами вектора ![]() . Они связаны с
координатами вектора формулами
. Они связаны с
координатами вектора формулами
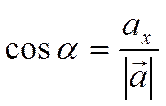 ,
, 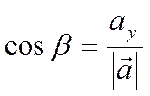 ,
,
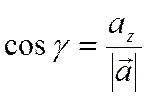 .
.
Отсюда следует соотношение
![]() .
.
Если концы вектора 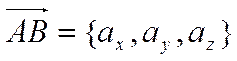 имеют координаты
имеют координаты ![]() ,
, ![]() ,
то координаты вектора
,
то координаты вектора 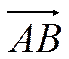 связаны с координатами
концов вектора соотношениями
связаны с координатами
концов вектора соотношениями
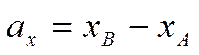 ,
,
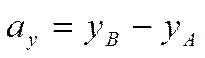 ,
,
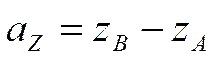 .
.
Пример.
Даны точки ![]() и
и ![]() .
Найти координаты вектора
.
Найти координаты вектора ![]() .
.
Решение.
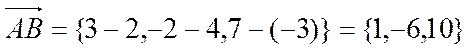 .
.
§4. Скалярное произведение векторов
Определение.
Пусть даны два ненулевых
вектора ![]() и
и ![]() .
Скалярным произведением векторов
.
Скалярным произведением векторов ![]() и
и ![]() называется число, обозначаемое
называется число, обозначаемое 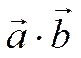 и равное
и равное
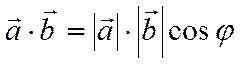 ,
,
где ![]() -
угол между векторами
-
угол между векторами ![]() и
и ![]() .
Если хотя бы один из векторов нулевой, то полагаем, что
.
Если хотя бы один из векторов нулевой, то полагаем, что ![]() .
При обозначении скалярного произведения точка часто опускается.
.
При обозначении скалярного произведения точка часто опускается.
Свойства скалярного произведения сформулируем в виде теоремы.
Теорема.
Свойства скалярного произведения.
1) ![]()
2) 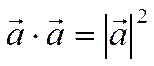
3) 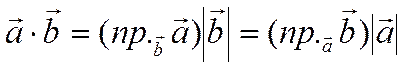
4) 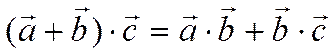
5) Если ![]() ,
,
![]() и
и ![]() -
орты осей координат, то
-
орты осей координат, то
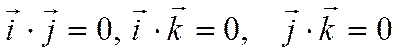 .
.
6) Если
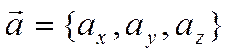 ,
,
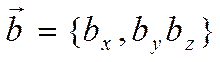 ,
,
то
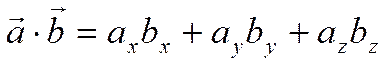 .
.
7) Векторы ![]() и
и ![]() взаимно
перпендикулярны тогда и только тогда, когда
взаимно
перпендикулярны тогда и только тогда, когда
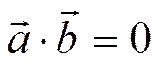
Доказательство.
Свойства 1, 2, 3, 5 следуют непосредственно из определения скалярного произведения. Свойство 4 следует из теоремы 10 о проекции суммы векторов. Действительно,
 .
.
Далее из свойств 4 и 5 получаем свойство 6. Имеем
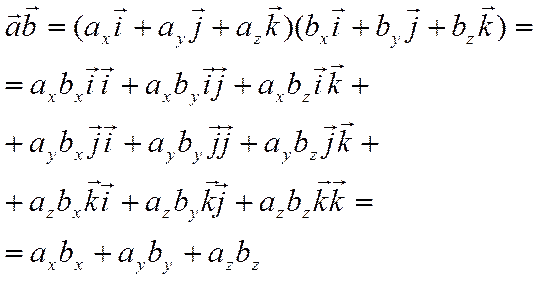
В последних равенствах учтено, что
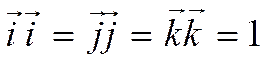 ,
,
а
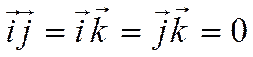 .
.
Рассмотрим свойство 7.
Если векторы ![]() и
и ![]() взаимно
перпендикулярны, то
взаимно
перпендикулярны, то
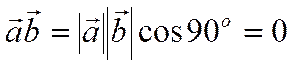 .
.
Если же
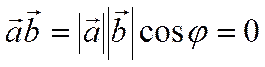 ,
,
где ![]() -
угол между векторами и
-
угол между векторами и ![]() и
и ![]() ненулевые
векторы, то
ненулевые
векторы, то ![]() . Отсюда
. Отсюда 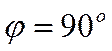 и
значит векторы
и
значит векторы ![]() и
и ![]() взаимно перпендикулярны. Таким
образом, чтобы ненулевые векторы
взаимно перпендикулярны. Таким
образом, чтобы ненулевые векторы ![]() и
и ![]() были взаимно перпендикулярны
необходимо и достаточно, чтобы выполнялось равенство
были взаимно перпендикулярны
необходимо и достаточно, чтобы выполнялось равенство 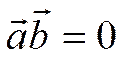 .
.
Из определения
скалярного произведения следует, что если ![]() и
и
![]() ненулевые векторы, то
ненулевые векторы, то
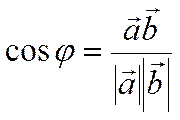 .
.
В свою очередь, зная координаты векторов, можно найти скалярное произведение и длины векторов. Таким образом, зная координаты векторов, можно найти косинус угла между векторами, а зная косинус можно найти и сам угол.
Пример.
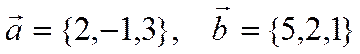 .
.
Найти угол между векторами.
Решение.
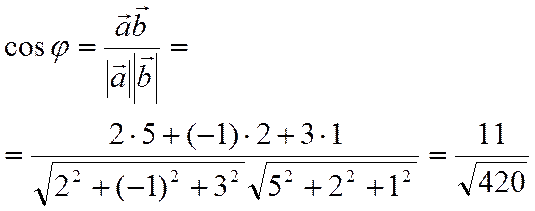
Отсюда
![]()
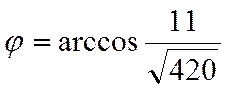 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.