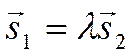 .
.
При этом, если прямые совпадают,
то тройка чисел ![]() , являющихся координатами
точки
, являющихся координатами
точки ![]() , будет решением уравнения прямой
, будет решением уравнения прямой ![]() . Если же прямые параллельны, то
тройка чисел
. Если же прямые параллельны, то
тройка чисел 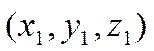 не будет решением
уравнения прямой
не будет решением
уравнения прямой ![]() , то есть при подстановке
этих чисел в уравнение прямой
, то есть при подстановке
этих чисел в уравнение прямой ![]() не будут
получены верные числовые равенства.
не будут
получены верные числовые равенства.
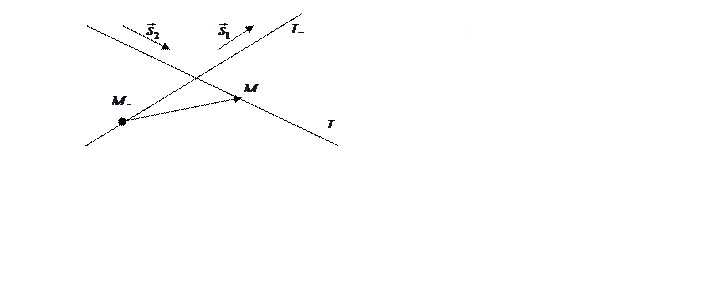
Рис. .35
Если направляющие
векторы прямых ![]() и
и ![]() не
коллинеарны, то прямые либо пересекаются в одной точке, либо скрещиваются.
не
коллинеарны, то прямые либо пересекаются в одной точке, либо скрещиваются.
Если прямые
пересекаются в одной точке, то либо точки ![]() и
и
![]() совпадают, то есть имеют равные
координаты, либо пересекаются в другой точке и тогда точки
совпадают, то есть имеют равные
координаты, либо пересекаются в другой точке и тогда точки 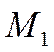 и
и 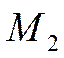 лежат
на разных прямых. В последнем случае векторы
лежат
на разных прямых. В последнем случае векторы ![]() и
и
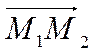 лежат в одной плоскости (смотри
Рис. 18), то есть компланарны. Условием же компланарнасти является равенство
нулю смешенного произведения этих векторов. Поэтому, если
лежат в одной плоскости (смотри
Рис. 18), то есть компланарны. Условием же компланарнасти является равенство
нулю смешенного произведения этих векторов. Поэтому, если
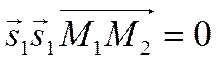 ,
,
то прямые пересекаются в одной точке. Если же смешанное произведение не равно нулю, то прямые скрещиваются.
Рассмотрим пример.
Пример.
Определить взаимное расположение прямых
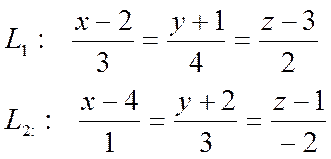 .
.
Направляющие векторы прямых ![]() и
и ![]() не
коллинеарны, так как если бы они были коллинеарны, то существовало бы число
не
коллинеарны, так как если бы они были коллинеарны, то существовало бы число ![]() такое, что справедливо векторное
равенство
такое, что справедливо векторное
равенство
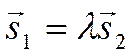 .
.
Или, в координатах
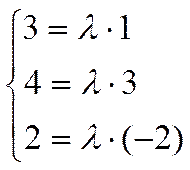 .
.
Но, как легко видеть, эта система
не совместна. Следовательно, прямые либо пересекаются в одной точке, либо
скрещиваются. Первая прямая проходит через точку ![]() ,
вторая через точку
,
вторая через точку ![]() , причем эти точки не
совпадают. Найдем смешанное произведение векторов
, причем эти точки не
совпадают. Найдем смешанное произведение векторов 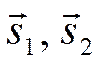 и
и
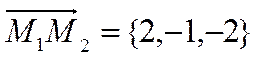
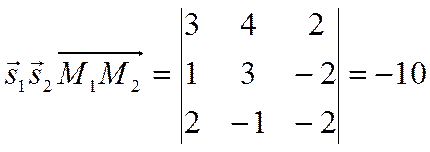 .
.
Так как смешанное произведение не равно нулю, то прямые скрещиваются.
Перейдем к рассмотрению
угла между прямыми в пространстве. Угол между двумя прямыми определяется как
угол между их направляющими векторами. При этом необходимо учесть, что в
зависимости от выбора направлений направляющих векторов угол между ними может
быть как острым, так и тупым (или прямым). Так, если в качестве направляющих
векторов (см. Рис. 18) выбрать ![]() и
и ![]() , то угол между ними будет острым.
Этот угол равен острому углу
, то угол между ними будет острым.
Этот угол равен острому углу ![]() между прямыми.
Если же в качестве направляющих векторов выбрать
между прямыми.
Если же в качестве направляющих векторов выбрать ![]() и
и
![]() , то угол между ними равен
, то угол между ними равен

Рис. 36.
тупому углу ![]() между прямыми. Косинус угла между
направляющими векторами можно определить через скалярное произведение по
формуле
между прямыми. Косинус угла между
направляющими векторами можно определить через скалярное произведение по
формуле
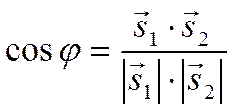
![]() .
.
![]()
При этом , если ![]() , то получаем, что угол
, то получаем, что угол ![]() острый угол между прямыми. Если же
острый угол между прямыми. Если же ![]() , то угол
, то угол ![]() является
тупым углом между прямыми. Однако, острый и тупой угол в сумме составляют 180o. Поэтому, найдя один из них, легко можно найти и
другой. Если же воспользоваться формулой
является
тупым углом между прямыми. Однако, острый и тупой угол в сумме составляют 180o. Поэтому, найдя один из них, легко можно найти и
другой. Если же воспользоваться формулой
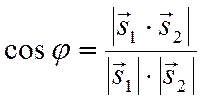 ,
,
то всегда будем получать острый
угол ![]() между прямыми (или прямой).
Рассмотрим пример.
между прямыми (или прямой).
Рассмотрим пример.
Пример.
Найти угол между прямыми
![]()
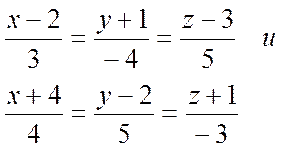 .
.
Направляющие векторы прямых равны
![]() и
и ![]() .
Следовательно, воспользовавшись формулой для нахождения косинуса острого угла,
получим
.
Следовательно, воспользовавшись формулой для нахождения косинуса острого угла,
получим
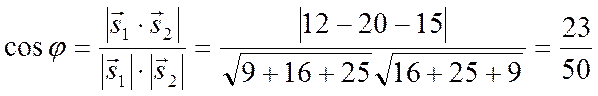 .
.
Тогда острый угол между прямыми равен
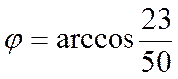
Глава 5. Взаимное расположение прямой и плоскости
Из элементарной геометрии известно, что возможны следующие варианты взаимного расположения прямой и плоскости в пространстве:
а) прямая лежит в плоскости;
б) прямая параллельна плоскости;
в) прямая пересекает плоскость в одной точке.
Выясним как по уравнениям прямой и плоскости определить их взаимное расположение.
Пусть плоскость ![]() задана уравнением
задана уравнением
![]() ,
,
а прямая ![]() задана
каноническим уравнением
задана
каноническим уравнением
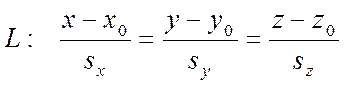 .
.
Тогда нормаль к плоскости равна 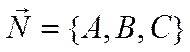 . Прямая проходит через точку
. Прямая проходит через точку ![]() и имеет направляющий вектор
и имеет направляющий вектор 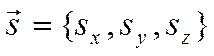 .
.
Если прямая лежит в
плоскости, то направляющий вектор прямой перпендикулярен нормали к плоскости.
Кроме того, точка ![]() должна принадлежать
плоскости и, следовательно, тройка чисел
должна принадлежать
плоскости и, следовательно, тройка чисел 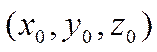 является
решением уравнения плоскости.
является
решением уравнения плоскости.
Таким образом, если 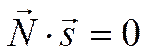 (условие перпендикулярности
векторов) и тройка чисел
(условие перпендикулярности
векторов) и тройка чисел 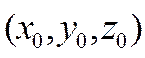 является
решением уравнения плоскости, то прямая лежит в плоскости. Если же
является
решением уравнения плоскости, то прямая лежит в плоскости. Если же 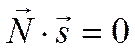 , но тройка чисел
, но тройка чисел 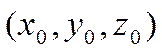 не является решением уравнения
плоскости, то прямая параллельна плоскости.
не является решением уравнения
плоскости, то прямая параллельна плоскости.
Если вектор ![]() не перпендикулярен вектору
не перпендикулярен вектору ![]() , то прямая пересекает плоскость в
одной точке. Рассмотрим на конкретном примере задачу о нахождении координат
точки пересечения прямой и плоскости.
, то прямая пересекает плоскость в
одной точке. Рассмотрим на конкретном примере задачу о нахождении координат
точки пересечения прямой и плоскости.
Пример.
Найти точку пересечения прямой
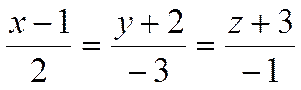
и плоскости
![]() .
.
Решение.
Задачу удобно решать, если уравнение прямой записать в параметрическом виде
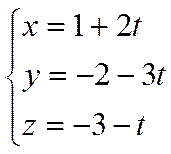 .
.
Так как точка пересечения прямой и плоскости принадлежит одновременно и прямой и плоскости, то ее координаты должны удовлетворять одновременно и уравнению плоскости и уравнениям прямой, то есть ее координаты должны удовлетворять системе уравнений
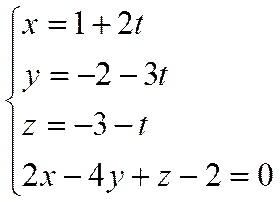
Решая систему, находим 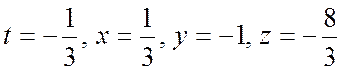 . Следовательно, точка пересечения
прямой и плоскости имеет координаты
. Следовательно, точка пересечения
прямой и плоскости имеет координаты 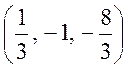 .
.
Если прямая пересекает
плоскость в одной точке и не перпендикулярна плоскости, то углом между прямой и
плоскостью называется острый угол ![]()
![]() (смотри Рис.18) между прямой и
проекцией прямой на плоскость. Если прямая перпендикулярна плоскости, то
полагают, что
(смотри Рис.18) между прямой и
проекцией прямой на плоскость. Если прямая перпендикулярна плоскости, то
полагают, что ![]() . Если же прямая
параллельна плоскости или лежит в плоскости, то полагают, что
. Если же прямая
параллельна плоскости или лежит в плоскости, то полагают, что ![]() . Выясним, как зная уравнения прямой
и плоскости, определить угол между прямой и плоскостью.
. Выясним, как зная уравнения прямой
и плоскости, определить угол между прямой и плоскостью.
Пусть плоскость ![]()
![]() задана
уравнением
задана
уравнением
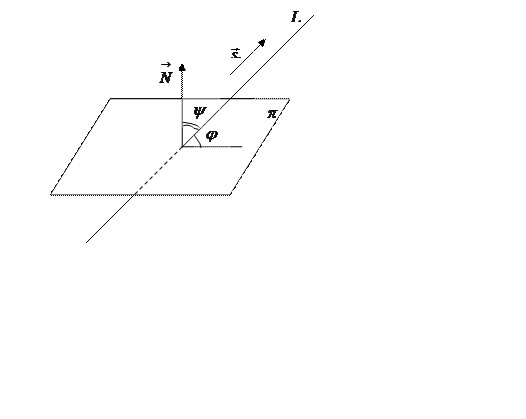
Рис. 37.
![]() ,
,
а прямая ![]() задана
каноническими уравнениями
задана
каноническими уравнениями
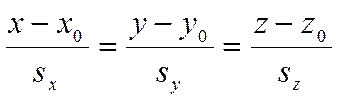 .
.
Тогда вектор нормали к плоскости
равен 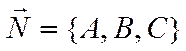 , а направляющий вектор прямой равен
, а направляющий вектор прямой равен
![]() . Косинус острого угла
. Косинус острого угла![]() между нормалью к плоскости и
направляющим вектором прямой (Рис. 18) можно найти используя скалярное
произведение по формуле
между нормалью к плоскости и
направляющим вектором прямой (Рис. 18) можно найти используя скалярное
произведение по формуле
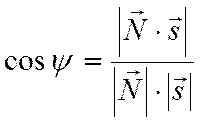 .
.
Отсюда
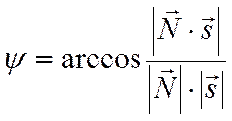 .
.
Тогда острый угол ![]() между прямой и плоскостью равен
(смотри Рис. 18)
между прямой и плоскостью равен
(смотри Рис. 18)
![]()
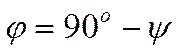 .
.
Рассмотрим пример.
Пример.
Найти угол между прямой
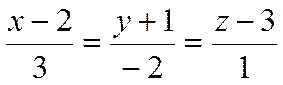
и плоскостью
![]() .
.
Решение.
Направляющий вектор прямой и нормаль к плоскости равны
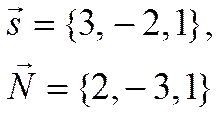
Тогда
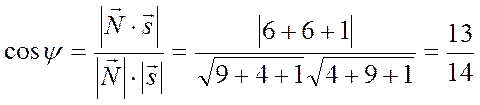 .
.
Отсюда
![]()
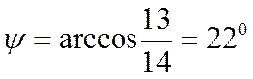 .
.
Тогда острый угол между прямой и плоскостью равен
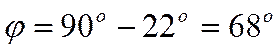 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.