Ниже рассматривается уравнение прямой на плоскости, проходящей через заданную точку и перпендикулярную заданному вектору.
Теорема.
Уравнение прямой,
проходящей через заданную точку 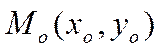 и
перпендикулярной заданному вектору
и
перпендикулярной заданному вектору 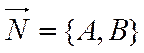 (нормаль к
прямой) имеет вид
(нормаль к
прямой) имеет вид
![]()
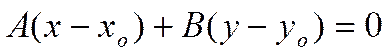 .
.
Доказательство.
Из элементарной
геометрии известно, что на плоскости через заданную точку 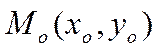 можно провести единственную прямую,
перпендикулярную заданному вектору
можно провести единственную прямую,
перпендикулярную заданному вектору 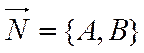 .
.
Рис. 34.
Докажем, что уравнение этой прямой имеет вид
![]() .
.
Пусть ![]() -
произвольная точка прямой, отличная от точки
-
произвольная точка прямой, отличная от точки ![]() .
Покажем, что ее координаты удовлетворяют уравнению
.
Покажем, что ее координаты удовлетворяют уравнению
 ,
,
то есть, что пара чисел ![]() есть решение этого уравнения. Из
рисунка 18 видно, что
есть решение этого уравнения. Из
рисунка 18 видно, что  и значит
и значит 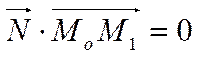 . Вектор
. Вектор 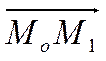 имеет
координаты
имеет
координаты
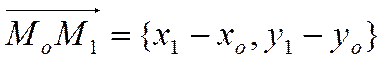 .
.
Следовательно, векторное равенство
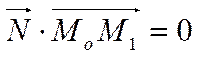
С учетом выражения скалярного произведения через координаты запишется в виде
![]() ,
,
то есть это выражение есть верное
числовое равенство. Но тогда пара чисел 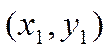 есть
решение уравнения
есть
решение уравнения
![]() ,
,
так как при подстановке вместо ![]() и
и ![]() в
это уравнение чисел
в
это уравнение чисел ![]() и
и ![]() ,
соответственно, получаем верное числовое равенство. Верное числовое равенство
также получается при подстановке пары чисел
,
соответственно, получаем верное числовое равенство. Верное числовое равенство
также получается при подстановке пары чисел ![]() (это
проверяется непосредственно). Итак, координаты любой точки прямой являются
решением этого уравнения. Докажем теперь обратное утверждение о том, что если
пара чисел
(это
проверяется непосредственно). Итак, координаты любой точки прямой являются
решением этого уравнения. Докажем теперь обратное утверждение о том, что если
пара чисел ![]() есть решение уравнения
есть решение уравнения
![]() ,
,
то точка ![]() лежит
на прямой. Доказательство будем проводить от противного. Допустим, что точка
лежит
на прямой. Доказательство будем проводить от противного. Допустим, что точка ![]() не лежит на прямой (см. рисунок 35).
не лежит на прямой (см. рисунок 35).

Рис.35 .
Тогда вектор 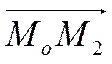 не лежит на прямой и не параллелен
прямой. Следовательно, вектор
не лежит на прямой и не параллелен
прямой. Следовательно, вектор ![]() не
перпендикулярен вектору
не
перпендикулярен вектору 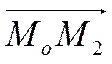 . Но тогда
. Но тогда
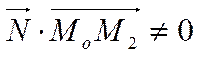
(условие неперпендикулярности двух векторов). В координатах это неравенство принимает вид
![]() .
.
Это означает, что пара чисел 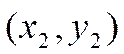 не есть решение уравнения
не есть решение уравнения
![]() .
.
Получили противоречие, так как по
предположению пара чисел ![]() есть решение
этого уравнения. Следовательно, верным является утверждение, что точка
есть решение
этого уравнения. Следовательно, верным является утверждение, что точка ![]() лежит на прямой. Теорема доказана.
лежит на прямой. Теорема доказана.
Рассмотрим пример.
Пример.
Записать уравнение
прямой, проходящей через точку ![]() и
перпендикулярной вектору
и
перпендикулярной вектору ![]() .
.
Решение.
Согласно доказанной выше теореме, уравнение имеет вид
![]()
или
![]() .
.
Если в рассмотренном выше уравнении прямой
![]()
раскрыть скобки, то уравнение примет вид
![]() .
.
Введя обозначение
![]() ,
,
получим уравнение в виде
![]() .
.
Покажем, что уравнение любой прямой можно записать в таком виде и, наоборот, что уравнение такого вида есть уравнение некоторой прямой на плоскости. Утверждение формулируем в виде теоремы.
Теорема 8.
Уравнение любой прямой на плоскости можно записать в виде
![]() ,
,
где хотя бы одно и чисел ![]() и
и ![]() отлично
от нуля, а вектор
отлично
от нуля, а вектор 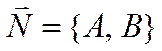 перпендикулярен прямой
(нормаль к прямой); и наоборот, уравнение вида
перпендикулярен прямой
(нормаль к прямой); и наоборот, уравнение вида
![]() ,
,
где хотя бы одно из чисел ![]() и
и ![]() отлично
от нуля, есть уравнение какой-то прямой на плоскости, причем вектор
отлично
от нуля, есть уравнение какой-то прямой на плоскости, причем вектор ![]() перпендикулярен этой прямой.
перпендикулярен этой прямой.
Доказательство.
Пусть на плоскости имеется
прямая. Из элементарной геометрии известно, что существует точка ![]() , лежащая на прямой и существует
ненулевой вектор
, лежащая на прямой и существует
ненулевой вектор 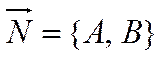 , перпендикулярный этой
прямой ( так как вектор ненулевой, то хотя бы одно из чисел
, перпендикулярный этой
прямой ( так как вектор ненулевой, то хотя бы одно из чисел ![]() и
и ![]() отлично
от нуля). Но тогда, как было показано выше, уравнение прямой имеет вид
отлично
от нуля). Но тогда, как было показано выше, уравнение прямой имеет вид
![]() .
.
Раскрывая скобки, получим
![]() .
.
Обозначим ![]() . Тогда уравнение примет вид
. Тогда уравнение примет вид
![]() ,
,
причем вектор 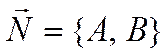 перпендикулярен прямой (нормаль к
прямой) и хотя бы одно из чисел
перпендикулярен прямой (нормаль к
прямой) и хотя бы одно из чисел ![]() и
и ![]() отлично от нуля. Следовательно,
уравнение любой прямой на плоскости можно записать в виде
отлично от нуля. Следовательно,
уравнение любой прямой на плоскости можно записать в виде
![]() ,
,
причем вектор ![]() отличен от нуля.
отличен от нуля.
Теперь докажем что уравнение вида
![]() ,
,
где хотя бы одно из чисел ![]() и
и ![]() отлично
от нуля, есть уравнение какой-то прямой. Пусть, например,
отлично
от нуля, есть уравнение какой-то прямой. Пусть, например, ![]() . Пусть
. Пусть ![]() -
произвольное число. Положим
-
произвольное число. Положим
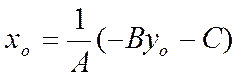
(так как ![]() ,
то
,
то ![]() существует). Непосредственной
подстановкой в уравнение нетрудно убедиться, что пара чисел
существует). Непосредственной
подстановкой в уравнение нетрудно убедиться, что пара чисел ![]() является решением рассматриваемого
уравнения. Следовательно выражение
является решением рассматриваемого
уравнения. Следовательно выражение
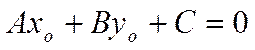
есть верное числовое равенство. Тогда уравнение
![]()
или, что то же самое
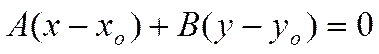
эквивалентно исходному уравнению
![]() .
.
Но, как было показано выше, уравнение
![]()
есть уравнение прямой, проходящей
через точку 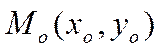 и перпендикулярной вектору
и перпендикулярной вектору ![]() . Следовательно, эквивалентное ему
уравнение
. Следовательно, эквивалентное ему
уравнение
![]()
также является уравнением этой же прямой.
Итак, доказано, что уравнение любой прямой на плоскости можно записать в виде
![]() ,
,
где 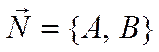 -
нормаль к прямой и наоборот, уравнение вида
-
нормаль к прямой и наоборот, уравнение вида
![]() ,
,
где хотя бы одно из чисел ![]() и
и ![]() отлично
от нуля, есть уравнение какой-то прямой на плоскости, причем вектор
отлично
от нуля, есть уравнение какой-то прямой на плоскости, причем вектор ![]() перпендикулярен этой прямой.
Уравнение прямой, записанное в таком виде, называется общим уравнением прямой.
перпендикулярен этой прямой.
Уравнение прямой, записанное в таком виде, называется общим уравнением прямой.
§2. Параметрические и канонические уравнения прямой на плоскости
Как известно из элементарной геометрии, на плоскости существует единственная прямая, проходящая через заданную току и коллинеарная заданному вектору. Уравнение такой прямой можно записать в виде так называемых параметрических уравнений прямой или канонического уравнения прямой, рассматриваемых ниже. Вначале рассмотрим параметрические уравнения прямой. Утверждение о возможности записи уравнения прямой на плоскости в виде параметрических уравнений сформулируем в виде теоремы.
Теорема.
Пусть прямая проходит через
точку ![]() и коллинеарна вектору
и коллинеарна вектору 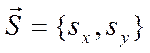 (т.е. вектор
(т.е. вектор ![]() либо
параллелен прямой, либо лежит на прямой). Тогда уравнения этой прямой можно
записать в виде
либо
параллелен прямой, либо лежит на прямой). Тогда уравнения этой прямой можно
записать в виде
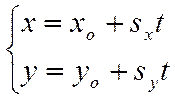 ,
,
где ![]() .
.
Утверждение о том, что эти уравнения являются уравнениями рассматриваемой прямой означает следующее:
1) если ![]() -
любая точка, лежащая на прямой, то существует число
-
любая точка, лежащая на прямой, то существует число ![]() такое,
что тройка чисел
такое,
что тройка чисел ![]() является решением
рассматриваемой системы уравнений;
является решением
рассматриваемой системы уравнений;
2) если тройка чисел ![]() есть любое решение рассматриваемой
системы, то точка
есть любое решение рассматриваемой
системы, то точка ![]() лежит на рассматриваемой
прямой.
лежит на рассматриваемой
прямой.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.