Как известно из
элементарной геометрии, прямую в пространстве можно рассматривать как линию
пересечения двух плоскостей. Пусть в пространстве имеется прямая ![]() . Возьмем точку
. Возьмем точку ![]() , не лежащую на прямой. Тогда через
прямую и точку
, не лежащую на прямой. Тогда через
прямую и точку ![]() можно провести плоскость
и притом только одну. Возьмем еще одну току
можно провести плоскость
и притом только одну. Возьмем еще одну току ![]() ,
не лежащую на прямой и отличную от точки
,
не лежащую на прямой и отличную от точки ![]() .
Тогда через прямую и точку
.
Тогда через прямую и точку ![]() можно провести
единственную плоскость
можно провести
единственную плоскость ![]() . Плоскости
. Плоскости ![]() и
и ![]() пересекаются
по прямой
пересекаются
по прямой ![]() (Рис. 18).
(Рис. 18).
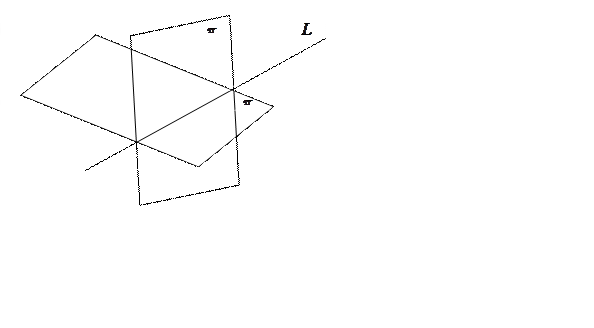
Рис. 33.
Пусть плоскости ![]() и
и ![]() имеют
уравнения:
имеют
уравнения:
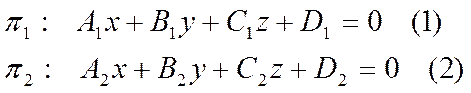
Рассмотрим какую-нибудь точку ![]() лежащую на прямой. Тогда она
одновременно принадлежит и плоскости
лежащую на прямой. Тогда она
одновременно принадлежит и плоскости ![]() и плоскости
и плоскости ![]() и следовательно тройка чисел
и следовательно тройка чисел ![]() является одновременно решением как
уравнения (1), так и уравнения (2), то есть является решением системы уравнений
является одновременно решением как
уравнения (1), так и уравнения (2), то есть является решением системы уравнений
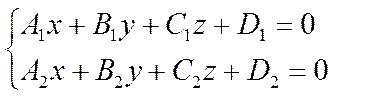 (3)
(3)
Обратно, пусть тройка чисел ![]() является решением системы (3).
Покажем, что в этом случае точка
является решением системы (3).
Покажем, что в этом случае точка ![]() лежит на прямой.
В самом деле, точка
лежит на прямой.
В самом деле, точка ![]() принадлежит плоскости
принадлежит плоскости ![]() так как тройка чисел
так как тройка чисел ![]() есть решение уравнения (1). Одновременно
точка
есть решение уравнения (1). Одновременно
точка ![]() принадлежит плоскости
принадлежит плоскости ![]() так как тройка чисел
так как тройка чисел ![]() есть решение уравнения (2).
Следовательно, точка
есть решение уравнения (2).
Следовательно, точка ![]() лежит на прямой
лежит на прямой ![]() так как она является общей для
плоскостей
так как она является общей для
плоскостей ![]() и
и ![]() .
.
Таким образом, мы
получили, что если точка ![]() лежит на
прямой, то тройка чисел
лежит на
прямой, то тройка чисел ![]() является
решением системы уравнений (3). И обратно, если тройка чисел
является
решением системы уравнений (3). И обратно, если тройка чисел ![]() является решением этой системы
уравнений, то точка
является решением этой системы
уравнений, то точка ![]() лежит на прямой
лежит на прямой ![]() .
.
В этом случае говорят, что система уравнений (3) является системой уравнений прямой в пространстве. Говорят также, что уравнения системы (3) являются общими уравнениями прямой в пространстве.
Произвольная система
уравнений вида (3) будет системой уравнений какой-то прямой в пространстве при
условии, что плоскости ![]() и
и ![]() ,
определяемые соответственно первым и вторым уравнением, не совпадают и не
параллельны. Условия параллельности и совпадения плоскостей были получены выше.
,
определяемые соответственно первым и вторым уравнением, не совпадают и не
параллельны. Условия параллельности и совпадения плоскостей были получены выше.
§2. Параметрические и канонические уравнения прямой в пространстве
Из элементарной геометрии известно, что через заданную точку в пространстве можно провести единственную прямую, коллинеарную заданному вектору. Ненулевой коллинеарный прямой вектор называется направляющим вектором прямой. Выведем уравнения прямой, заданной этими условиями.
Итак, пусть прямая
проходит через точку ![]() и коллинеарна вектору
и коллинеарна вектору 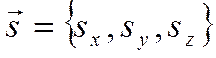 (Рис.18).
(Рис.18).
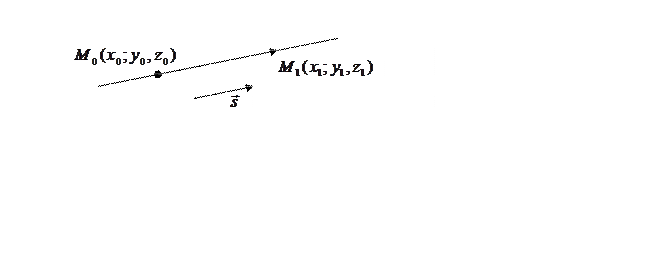
Рис. 34.
Возьмем на прямой еще одну точку ![]() . Тогда вектор
. Тогда вектор 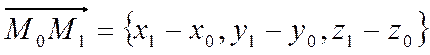 коллинеарен вектору
коллинеарен вектору ![]() и значит существует число
и значит существует число ![]() такое, что выполняется равенство
(условие коллинеарности векторов
такое, что выполняется равенство
(условие коллинеарности векторов
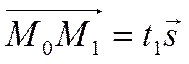 .
.
Из этого векторного равенства следует, что одновременно верны следующие числовые равенства для координат этих векторов
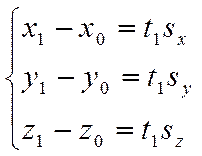 (4)
(4)
А это означает, что четверка
чисел ![]() является решением системы уравнений
является решением системы уравнений
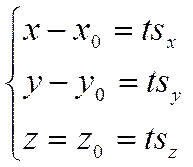
Или
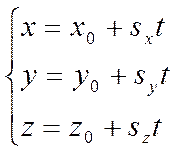 (5)
(5)
Непосредственной подстановкой
легко убедиться, что четверка чисел ![]() также является
решением этой системы уравнений. Итак, какова бы ни была точка
также является
решением этой системы уравнений. Итак, какова бы ни была точка ![]() , лежащая на прямой, найдется
число
, лежащая на прямой, найдется
число ![]() такое, что четверка чисел
такое, что четверка чисел ![]() является решением системы уравнений
(5). Можно также доказать (аналогично тому, как это было доказано для прямой на
плоскости), что если четверка чисел
является решением системы уравнений
(5). Можно также доказать (аналогично тому, как это было доказано для прямой на
плоскости), что если четверка чисел ![]() является
решением системы (5) то точка
является
решением системы (5) то точка ![]() лежит на прямой
лежит на прямой
![]() . Уравнения системы (5) называются
параметрическими уравнениями прямой.
. Уравнения системы (5) называются
параметрическими уравнениями прямой.
Пример.
Записать параметрические
уравнения прямой, проходящей через точку ![]() и
коллинеарной вектору
и
коллинеарной вектору ![]() .
.
Решение.
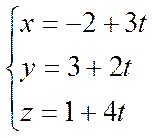 .
.
Снова вернемся к ситуации,
когда прямая проходит через точку ![]() , коллинеарна
вектору
, коллинеарна
вектору ![]() и на прямой взята еще одна точка
и на прямой взята еще одна точка ![]() , не совпадающая с точкой
, не совпадающая с точкой ![]() . Тогда, как показано выше,
существует число
. Тогда, как показано выше,
существует число ![]() такое, что одновременно
верны равенства
такое, что одновременно
верны равенства
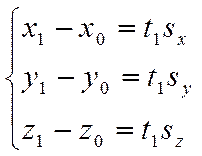
Пусть, кроме того, ни одна из
координат вектора ![]() не равна нулю, то есть
не равна нулю, то есть ![]() . Тогда систему равенств можно
записать в виде
. Тогда систему равенств можно
записать в виде
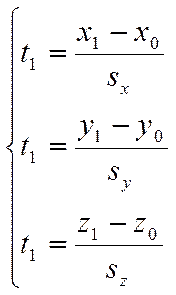 .
.
Из этой системы верных равенств следует, что одновременно верны равенства
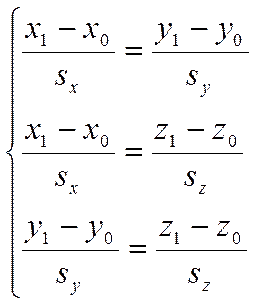 .
.
Каждое из этих трех равенств является следствием двух других. Поэтому достаточно рассмотреть, например, систему равенств
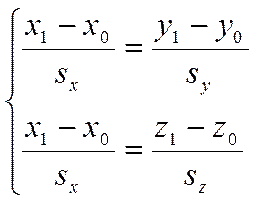 .
.
Но если эти равенства верные, то
тройка чисел ![]() является решением системы
уравнений
является решением системы
уравнений
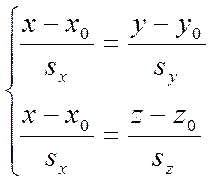 (6)
(6)
Непосредственной подстановкой
легко убедиться, что этой системе уравнений удовлетворяет также тройка чисел ![]() . Таким образом, если
. Таким образом, если ![]() есть произвольная точка прямой и
одновременно
есть произвольная точка прямой и
одновременно ![]() , то тройка чисел
, то тройка чисел ![]() является решением системы уравнений
(6). Можно показать (аналогично тому, как это сделано для прямой на плоскости),
что если тройка числе
является решением системы уравнений
(6). Можно показать (аналогично тому, как это сделано для прямой на плоскости),
что если тройка числе ![]() есть решение системы (6),
то точка
есть решение системы (6),
то точка ![]() лежит на прямой. Таким образом,
система уравнений (6) есть система уравнений прямой в пространстве. Вместо
системы уравнений (6) можно записать эквивалентную ей систему, например,
лежит на прямой. Таким образом,
система уравнений (6) есть система уравнений прямой в пространстве. Вместо
системы уравнений (6) можно записать эквивалентную ей систему, например,
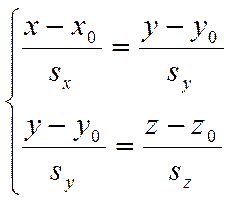 .
.
Эти системы принято записывать в виде двойного равенства
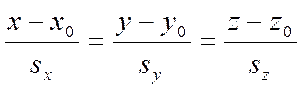 ,
,
из которых следует любая из эквивалентных систем. Уравнения прямой, записанные в таком виде, называются каноническими уравнениями прямой в пространстве.
Пример.
Прямая проходит через
точку ![]() и коллинеарна вектору
и коллинеарна вектору ![]() . Записать каноническое уравнение
прямой.
. Записать каноническое уравнение
прямой.
Решение.
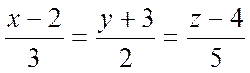 .
.
Замечание.
При выводе уравнения
прямой в каноническом виде предполагалось, что ни одна из координат
направляющего вектора 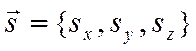 не равна нулю,
так как в противном случае в знаменателе канонических уравнений прямой появятся
нули и уравнение не будет иметь смысла. Тем не менее, если одна или две
координаты вектора
не равна нулю,
так как в противном случае в знаменателе канонических уравнений прямой появятся
нули и уравнение не будет иметь смысла. Тем не менее, если одна или две
координаты вектора ![]() (но не все три) равны
нулю, то условно применяют запись того же вида, что и при не равных нулю всех
координат вектора
(но не все три) равны
нулю, то условно применяют запись того же вида, что и при не равных нулю всех
координат вектора ![]() . Такая запись также
называется каноническими уравнениями прямой. Рассмотрим пример.
. Такая запись также
называется каноническими уравнениями прямой. Рассмотрим пример.
Пример.
Прямая проходит через
точку ![]() и имеет направляющий вектор
и имеет направляющий вектор ![]() . Тогда выражение
. Тогда выражение
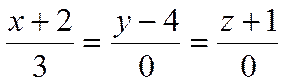
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.