Снова возьмем на прямой две точки
![]() и
и ![]() как
показано на рисунке 43. Из рисунка следует, что
как
показано на рисунке 43. Из рисунка следует, что ![]() .
Далее, из рисунка видно, что
.
Далее, из рисунка видно, что
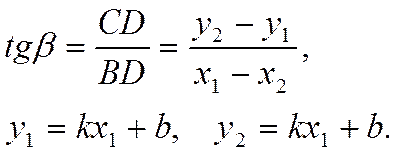
![]()
Тогда
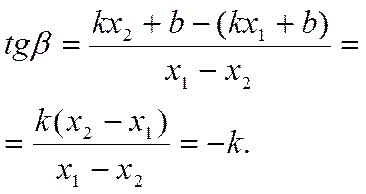
Так как ![]() ,
то
,
то
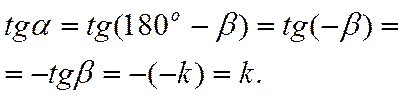
Таким образом, и в этом случае
![]()
Заметим, что в случае, когда
![]() ,
,
тангенс угла наклона прямой
отрицателен и значит ![]() . Наконец, если угол
наклона равен нулю, то есть прямая параллельна оси
. Наконец, если угол
наклона равен нулю, то есть прямая параллельна оси ![]() ,
то
,
то
![]()
С другой стороны, уравнение прямой в этом случае имеет вид
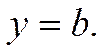
В самом деле, если уравнение
![]()
записать в виде
![]() ,
,
то видно, что вектор нормали к
этой прямой равен 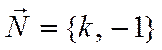 . Но если прямая
параллельна оси
. Но если прямая
параллельна оси ![]() , то вектор
, то вектор ![]() коллинеарен вектору
коллинеарен вектору ![]() . Следовательно
. Следовательно
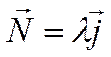 .
.
Отсюда следует, что ![]() и уравнение прямой имеет вид
и уравнение прямой имеет вид
![]() .
.
Следовательно, и в этом случае ![]() и
и ![]() ,
то есть
,
то есть ![]() .
.
Пример.
Уравнение прямой имеет вид
![]() .
.
Найти угол наклона прямой.
Решение.
Обозначим угол
наклона через ![]() . Тогда
. Тогда ![]() . Следовательно
. Следовательно
![]() .
.
Запишем в виде теоремы условия параллельности и перпендикулярности прямых, заданных уравнениями с угловым коэффициентом.
Теорема
Пусть прямые ![]() и
и ![]() заданы
уравнениями с угловым коэффициентом:
заданы
уравнениями с угловым коэффициентом:
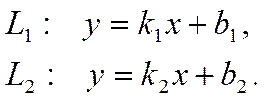
Эти прямые параллельны тогда и
только тогда, когда ![]() (при условии, что
(при условии, что 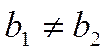 ; если
; если 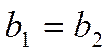 ,
то прямые совпадают). Прямые перпендикулярны тогда и только тогда, когда
,
то прямые совпадают). Прямые перпендикулярны тогда и только тогда, когда ![]() .
.
Доказательство.
Уравнения прямых можно записать в виде
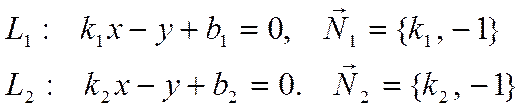
Вначале докажем условие
параллельности. Если прямые параллельны, то векторы нормалей ![]() и
и 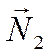 коллинеарны,
то есть существует такое число
коллинеарны,
то есть существует такое число ![]() , что
, что
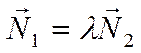 .
.
Отсюда следует равенство координат
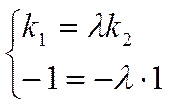 .
.
Следовательно ![]() и
и ![]() .
.
Обратно, если 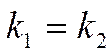 , то векторы нормалей равны и значит
прямые параллельны (при условии, что
, то векторы нормалей равны и значит
прямые параллельны (при условии, что 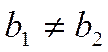 .
.
Теперь рассмотрим условие перпендикулярности. Прямые перпендикулярны тогда и только тогда, когда перпендикулярны векторы нормалей, то есть
![]()
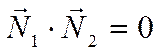 .
.
Или, в координатах,
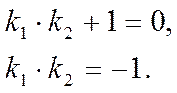
Что и требовалось доказать.
Пример.
Доказать, что прямые
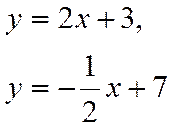
перпендикулярны.
Решение.
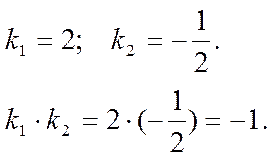
Следовательно, прямые перпендикулярны.
Получим выражение для угла между прямыми в случае, когда прямые заданы уравнениями с угловым коэффициентом. Утверждение сформулируем в виде теоремы.
Теорема.
Пусть прямые ![]() и
и 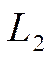 заданы
уравнениями с угловым коэффициентом:
заданы
уравнениями с угловым коэффициентом:
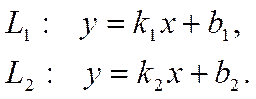
Тогда тангенс острого угла межу прямыми выражается по формуле
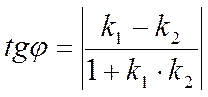 .
.
Доказательство.
Уравнения прямых запишем в виде
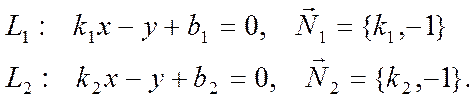
Здесь ![]() и
и
![]() - векторы нормалей между прямыми.
Как было показано выше, косинус острого угла между прямыми можно найти по
формуле
- векторы нормалей между прямыми.
Как было показано выше, косинус острого угла между прямыми можно найти по
формуле
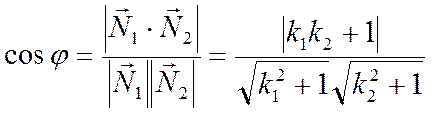 .
.
С учетом соотношения
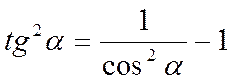
получаем
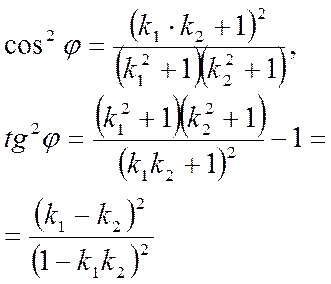
Тогда, с учетом того, что тангенс острого угла есть число положительное, получаем
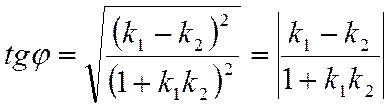
![]() .
.
(т.е. инеарна вектору одит через точку виде теоремы. рассматриваемых ниже.х
Глава 3. Плоскость в пространстве.
§1. Уравнение плоскости в пространстве
Определение.
Уравнением с тремя неизвестными называется выражение вида
![]()
например,
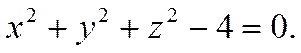
Определение.
Решением уравнения ![]() называется любая упорядоченная
тройка чисел
называется любая упорядоченная
тройка чисел 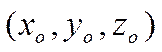 такая, что при подстановке
вместо
такая, что при подстановке
вместо ![]() и
и ![]() чисел
чисел
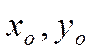 и
и ![]() ,
соответственно, получается верное числовое равенство. Например, тройка чисел
,
соответственно, получается верное числовое равенство. Например, тройка чисел ![]() является решением уравнения
является решением уравнения
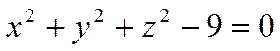
так как при подстановке этих чисел в уравнение получается верное числовое равенство.
Далее будем всегда
предполагать, что в пространстве задана Декартова система координат. Тем самым,
между тройками чисел ![]() и точками пространства
установлено взаимно однозначное соответствие.
и точками пространства
установлено взаимно однозначное соответствие.
Определение.
Уравнение вида ![]() называется уравнением поверхности в
пространстве если выполнено следующее:
называется уравнением поверхности в
пространстве если выполнено следующее:
1) Пусть точка ![]() лежит на поверхности. Тогда тройка
чисел
лежит на поверхности. Тогда тройка
чисел ![]() является решением уравнения.
является решением уравнения.
2) Пусть тройка чисел ![]() является решением уравнения, тогда
точка
является решением уравнения, тогда
точка ![]() лежит на рассматриваемой
поверхности.
лежит на рассматриваемой
поверхности.
Ниже будем рассматривать один из видов поверхностей, а именно плоскость. При рассмотрении плоскости будем опираться на понятия и утверждения, рассматриваемые в элементарной (школьной) геометрии.
Из элементарной геометрии известно, что существует единственная плоскость, проходящая через заданную точку и перпендикулярная заданному вектору. Выведем уравнение этой плоскости. Утверждение сформулируем в виде теоремы.
Теорема.
Уравнение плоскости,
проходящей через заданную точку ![]() и
перпендикулярной заданному вектору
и
перпендикулярной заданному вектору ![]() (нормаль к
плоскости) имеет вид
(нормаль к
плоскости) имеет вид
![]() .
.
Доказательство.
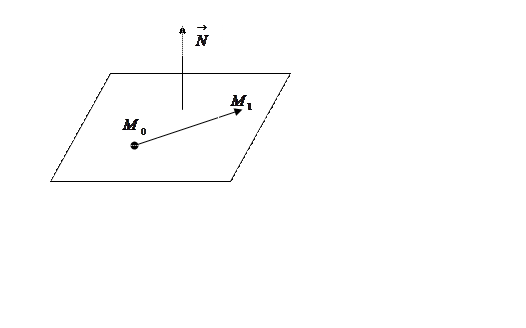
Рис. 44.
Пусть плоскость проходит
через заданную точку ![]() и перпендикулярна
заданному вектору
и перпендикулярна
заданному вектору ![]() . Возьмем на плоскости
произвольную точку
. Возьмем на плоскости
произвольную точку ![]() , отличную от точки
, отличную от точки ![]() . Тогда из элементарной геометрии
следует, что вектор
. Тогда из элементарной геометрии
следует, что вектор 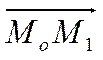 перпендикулярен вектору
перпендикулярен вектору ![]() . Следовательно,
. Следовательно,
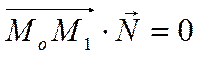 .
.
Поскольку
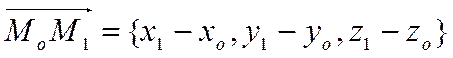 ,
,
получаем, что равенство, выражающее скалярное произведение в координатной форме
![]()
![]()
является верным числовым
равенством. А это означает, что тройка чисел ![]() является
решением уравнения
является
решением уравнения
![]() .
.
Непосредственной подстановкой в
уравнение легко убедиться, что тройка чисел 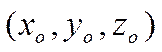 также
является решением этого уравнения. Таким образом, если точка лежит на
плоскости, то ее координаты образуют решение рассматриваемого уравнения.
также
является решением этого уравнения. Таким образом, если точка лежит на
плоскости, то ее координаты образуют решение рассматриваемого уравнения.
Докажем теперь, что если тройка чисел есть решение рассматриваемого уравнения, то точка, координаты которой есть эти числа, лежит на плоскости.
Пусть тройка чисел ![]() есть решение уравнения
есть решение уравнения
![]() ,
,
то есть
![]()
есть верное числовое равенство.
Докажем, что точка ![]()
![]() принадлежит
плоскости. Доказательство проведем от противного. Допустим, что точка
принадлежит
плоскости. Доказательство проведем от противного. Допустим, что точка ![]() не лежит на плоскости (Рис. 45)
не лежит на плоскости (Рис. 45)
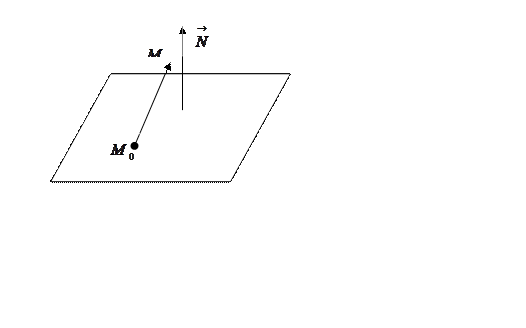
Рис. 45.
Из элементарной геометрии следует, что вектор
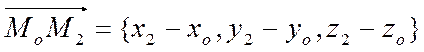
не перпендикулярен вектору ![]() . Тогда равенство
. Тогда равенство
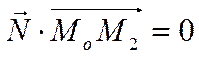
не является верным числовым равенством. Или соответствующее равенство для координат
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.