Основные понятия векторной алгебры. Проекция вектора на ось. Координаты вектора. Скалярное произведение векторов, страница 3

           Проекцию вектора на ось можно выразить через длину вектора и косинус угла между вектором и осью. Имеет место следующая теорема.

Теорема 8.

         Пусть даны вектор  и ось . Пусть  - угол между вектором и осью. Тогда

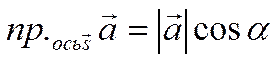.       (3)

Доказательство.

       Обозначим через  вектор-проекцию вектора   на ось. 1)Пусть 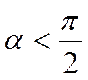 . Тогда, как видно из рисунка 14,  вектор-проекция   и ось   сонаправлены. Следовательно, как видно из рисунка,

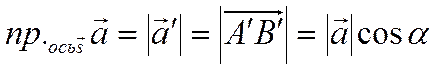
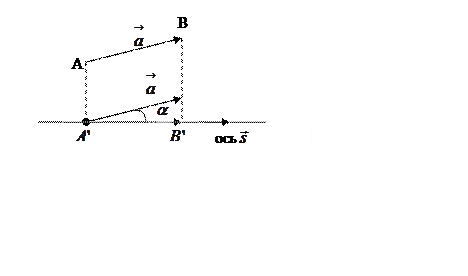
Рис. 14.

2) Пусть 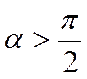. В этом случае, как видно из рисунка 15,

                                          Рис.15.

вектор-проекция   и ось противонаправлены. Следовательно 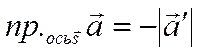. Но, как видно из рисунка 18,

.

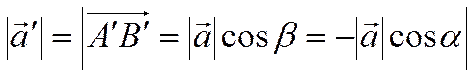Здесь учтено, что . Тогда

.

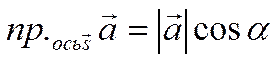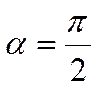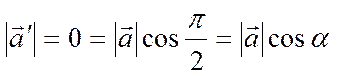3) Если , то . Следовательно, и в этом случае верна формула (3).

         Рассмотрим теорему, устанавливающую связь вектор-проекции вектора на ось с его проекцией на эту же ось.

        Предварительно введем понятие орта вектора.

Определение.

         Пусть  ненулевой вектор. Ортом вектора  будем называть вектор единичной длины, коллинеарный и сонаправленный с вектором  .Орт вектора  будем обозначать как .

Из самого определения орта вектора следует, что для любого ненулевого вектора  имеет место равенство 

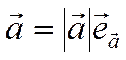
Имеет место следующая теорема.

Теорема 9.

         Вектор-проекция любого вектора на ось равна произведению проекции вектора на эту ось на орт оси, то есть

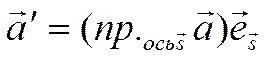,      (4)

Где - вектор-проекция вектора   на ось ,  -орт оси .

Доказательство.

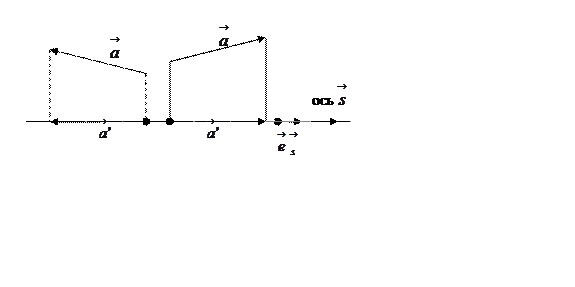
Рис. 16.

Как видно из рисунка 16, если сонаправлен с осью , то из определения проекции и вектор-проекции вектора на ось следует, что

.

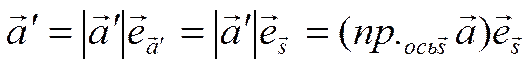Здесь учтено, что 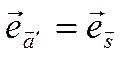.  Если противонаправлен оси , то

.

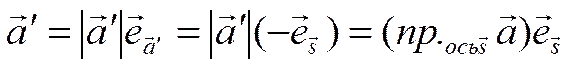В последних равенствах учтено, что 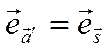 и  .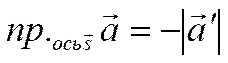

         Рассмотрим  связь проекции суммы векторов с проекциями слагаемых.

Теорема 10.

Пусть 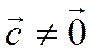. Тогда  для  любых  и 

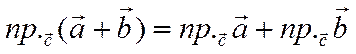
Доказательство.

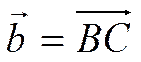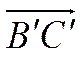            Пусть  .  Вектор отложим от точки и обозначим его   , т.е. . Проведем через вектор  прямую. Получим ось, которую обозначим ось . Пусть и   - вектор-проекции векторов  и 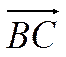 на ось .  Тогда 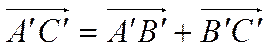  есть вектор-проекция вектора  на ось . При этом возможны следующие варианты:

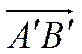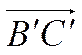1) и   сонаправлены с осью .

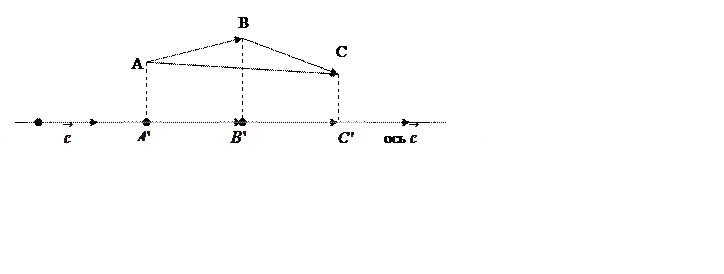
           Рис. 17.

2) 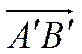 сонаправлен,  а 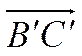 противонаправлен  оси .

3) 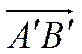противонаправлен , а 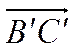 сонаправлен с осью .

4) 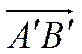 противонаправлен оси и  противонаправлен оси .

         Первый из возможных вариантов изображен на рисунке 18. Из рисунка видно, что

.

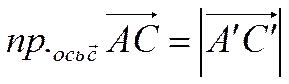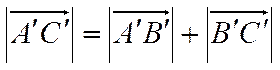
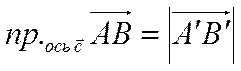
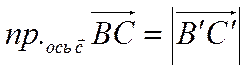
Следовательно

.

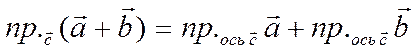Оставшиеся варианты рассматриваются аналогично. Рассмотрим, например 2-й вариант. Из рисунка 18 видно, что

        Рис. 18.

.

.

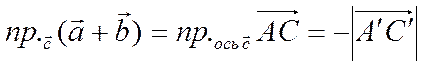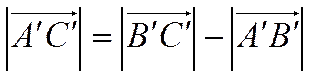Следовательно

.

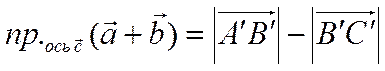Из этого же рисунка видно, что

,

.

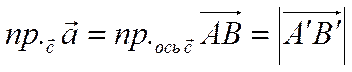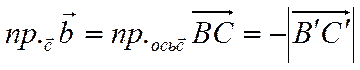Отсюда следует, что

.

     

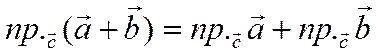§3. Координаты вектора

           До   сих пор считалось, что векторы рассматриваются в пространстве. Начиная с этого момента будим считать, что все векторы рассматриваются на плоскости. Будем также полагать, что на плоскости задана Декартова система координат (даже если об этом не говорится), представляющая две взаимно перпендикулярные числовые оси – горизонтальная ось и вертикальная ось . Тогда каждой точке на плоскости ставится в соответствие пара чисел 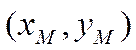, которые являются ее координатами. Обратно, каждой паре чисел  соответствует точка плоскости такая, что пара чисел  являются ее координатами.

Рис. 19.

        Из элементарной геометрии известно, что если на плоскости имеются две точки  и 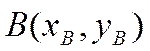 , то расстояние между этими точками выражается через их координаты по формуле

.

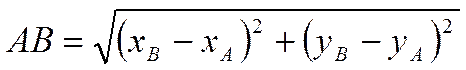         Пусть на плоскости задана Декартова система координат. Орт оси  будем обозначать символом , а орт оси символом .  Проекцию  произвольного вектора  на ось  будем обозначать символом 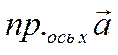, а проекцию на ось символом  .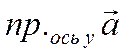

     

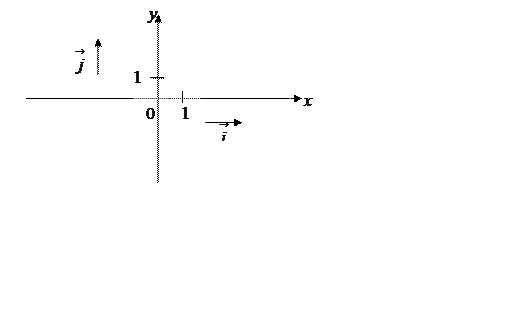
                                                Рис. 20.

       Пусть  - произвольный вектор на плоскости. Имеет место следующая теорема.

Теорема 22.

         Для любого вектора  на плоскости существует пара чисел 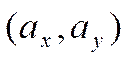  таких, что справедливо равенство

.

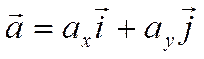При этом ,  .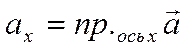

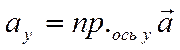Доказательство.

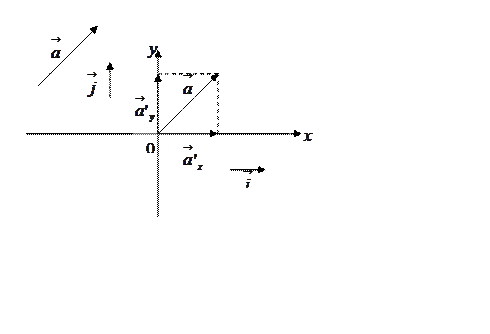
Рис. 21.

       Пусть дан вектор. Отложим вектор   от начала координат. Обозначим через   вектор-проекцию вектора  на ось , а через  вектор-проекцию вектора  на ось  . Тогда, как видно из рисунка 21, имеет место равенство

.

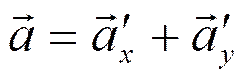Согласно теореме 9,

,

.

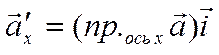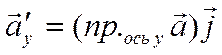Обозначим 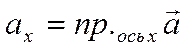  ,   . Тогда получаем

.

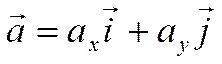Итак, доказано, что для любого вектора  существует пара чисел 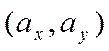  таких, что справедливо равенство

,

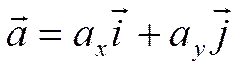Причем,

,

.

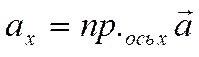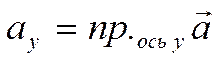При другом расположении вектора   относительно осей доказательство аналогично.

Определение.

           Пара чисел  и   таких, что 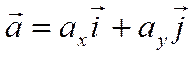, называются координатами вектора . Число  называется иксовой координатой, а число  игрековой координатой.

Определение.

         Пара ортов осей координат 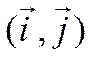 называется ортонормированным базисом на плоскости. Представление любого вектора  в виде 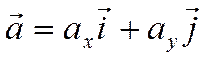 называется разложением вектора  по базису .

         Непосредственно из определения координат вектора следует, что если координаты векторов равны, то равны и сами векторы. Справедливо также и обратное утверждение.

Теорема.

       Равные векторы имеют равные координаты.

Доказательство.

      Пусть

,

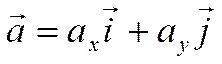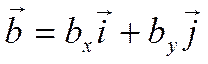
и 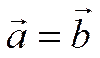 . Докажем, что  ,  .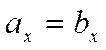

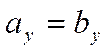Из равенства векторов следует, что

.

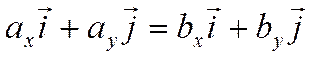Отсюда

.

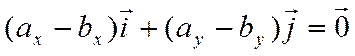Допустим, что 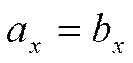, а  .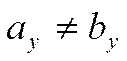

Тогда 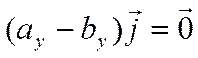  и значит 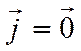, что не верно. Аналогично, если  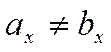, но , то  .  Отсюда 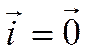,  что не верно. Наконец, если допустить, что 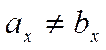  и 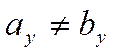 , то получаем, что

.

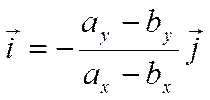Это означает, что векторы и  коллинеареы. Но это не верно, так как они перпендикулярны. Следовательно, остается, что , , 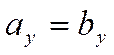что и требовалось доказать.

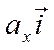        Таким образом, координаты вектора полностью определяют сам вектор. Зная координаты  и вектора   можно построить сам вектор   , построив векторы  и 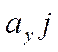  и сложив их. Поэтому часто сам вектор   обозначают в виде пары его координат и пишут . Такая запись означает, что  .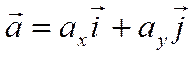

        Непосредственно из определения координат вектора следует следующая теорема.

Теорема.