Методическое руководство к практическим занятиям по курсу "Основы математической теории надежности и её приложения к задачам электроэнергетики"

                                   ПРЕДИСЛОВИЕ

   Методическое руководство к практическим занятиям по курсу "Основы математической теории надежности и её приложения к задачам электроэнергетики" представляет собой сборник задач для индивидуальной работы над разделами курса. Как правило, типовые задачи решаются лектором во время чтения курса.Практическое же освоение студентами материала основывается на выполнении ими индивидуальных заданий по соответствующим разделам курса.Объем каждого задания ориентирован на его выполнение в течение двух академических часов аудиторных занятий.Задания могут выполняться как во время аудиторных занятий, так и вне аудитории с последующей сдачей задания на очередном занятии  или консультации.

   Вследствие ограниченного объема настоящего руководства в нем отсутствуют сведения из теории, изложенные , в частности, в учебном пособии " Основы математической теории надежности   и её приложения к задачам электроэнергетики" [1], в котором даются ссылки и на другие источники в  части как математической теории надежности , так и её приложений к задачам электроэнергетики. По каждому из разделов руководства приведено решение типовых задач и даны задачи для индивидуальной работы студента под контролем преподавателя.

   Материал руководства может быть также использован и для самостоятельной работы над курсом как студентами, так и аспирантами электроэнергетических специальностей.

   При написании настоящей работы автор основывался на  опыте преподавания данной дисциплины в Санкт-Петербургском и Новосибирском государственных технических университетах, а также на опыте научной работы , связанной с вопросами, составляющими предмет курса.

                                    ОГЛАВЛЕНИЕ

                                                                                                                         Стр.

  1.Надежность элемента и системы, эксплуатируемых до первого отказа

  2.Надежность системы с зависимыми элементами . . . . . . . . . . . . . . . . .

  3.Надежность восстанавливаемого элемента . . . . . . . . . . . . . . . . . . . . . .

3.1 Время восстановления элемента пренебрежимо мало . . . . . . . . . .

3.2 Время восстановления элемента соизмеримо со временем его

           эксплуатации до отказа ........ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

4. Резервирование в технических системах . . . . . . . . . . . . . . . . . . . . . . .

5. Законы распределения сроков службы стареющих элементов . . . . . .

6. Предупредительные замены стареющих элементов . . . . . . . . . . . . . . .

  7. Определение сроков службы стареющих элементов . . . . . . . . . . . . . .

      1. НАДЕЖНОСТь ЭЛЕМЕНТА И СИСТЕМЫ,ЭКСПЛУАТИРУЕМОЙ

                                        ДО ПЕРВОГО ОТКАЗА

                                   Типовые задачи с решениями

   Во всех вариантах первой задачи задания приняты следующие допущения:

n функции надежности всех единичных элементов , входящих в систему, описываются экспоненциальным законом при интенсивности  отказов l₁;

n резервные элементы эксплуатируются совместно с рабочими элементами и имеют те же характеристики надежности, что и рабочие элементы ;

n число элементов, включенных в смысле надежности последовательно, обозначено ;

n число цепочек, включенных в смысле надежности параллельно, включающее в себя как рабочие , так и резервные цепочки, обозначено s;

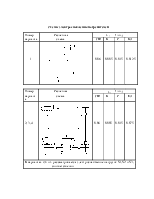
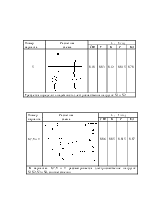
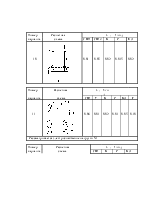
n приняты следующие обозначения для схем включения резервных

       цепочек:

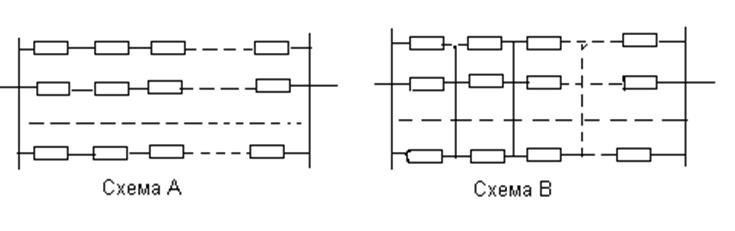
                Рис.1.1  Возможные схемы включения резервных цепочек

   1.1. Система состоит из 8 равнонадежных элементов, соединенных в  смысле надежности последовательно, при этом вероятность безотказной эксплуатации элемента после 8 лет эксплуатации  составляет Р(8)=0.80. Для повышения надежности эксплуатации система дополняется двумя параллельными цепочками , подключаемыми по схемам А или В . Определить вероятности безотказной эксплуатации нерезервированной системы , а также систем, резервированных по схемам А и В , при t=8 лет. Для всех трех систем определить также средние времена их эксплуатации до первого отказа.

   Решение. При последовательном соединении равнонадежных  элементов , характеризующихся экспоненциальным законом надежности ,  функция надежности системы определяется как :

                                        Р(t)=0.8⁸=0.168.

   При подключении двух резервных цепочек по схемам А и В функции         надежности резервированных систем запишутся в виде:

                          Р_А(t)= 1-(1-P(t))^s =1-(1-0.8⁸)³ =0.424,

                          P_B(t)=(1-(1-P₁(t))^s)=(1-(1-0.8)³)⁸=0.938.

  Среднее время эксплуатации системы до её первого отказа определяется как:

                                     T_ср=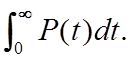

   В рассматриваемой задаче

                                      T_ср^н/р=,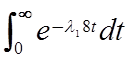

где- интенсивность отказа единичного элемента, определяемая из условия:

                               Р₁(8)==0,8;  =0.0279 1/год.

     Следовательно,   T_ср^н/р = 1/l₁*8= 4.48 года.

   Среднее время эксплуатации системы, резервированной по схеме А,определяется как

   T_ср^A=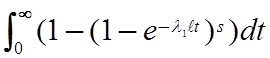=T_ср^н/р(1+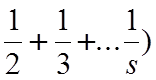= 4.48´1.833=8.2 года.

   Среднее время эксплуатации системы, резервированной по схеме В,будет

  T_ср^В=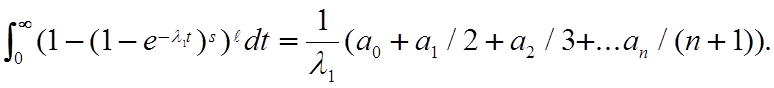   (1.1)

   В выражении (1)    () 

                 при (k+1)s-1³ i ³ ks , n=s - 1.

   В рассматриваемой схеме

   T_ср^В=(1+1/2+1/3-7/4-7/5-7/6+21/7+21/8+21/9-35/10-35/11-35/12+35/13 +35/14+35/15-21/16-21/17-21/18+7/19+7/20+7/21-1/22-1/23-1/24)=21.82 года.

   Из приведенного примера видно, что резервирование по схеме В приводит к увеличению среднего срока службы системы по сравнению с резервированием по схеме А в 2.66 раза.

1.2 Система состоит из 6 равнонадежных элементов, соединенных в смысле надежности последовательно.Функция надежности единичного элемента к моменту времени t=10 часов составляет Р₁(t)=0.80. Определить необходимое число резервных цепочек , соединенных по схемам А и В, чтобы функции надежности резервированных систем к моменту времени t=10 часов

     Р(t)³0.95. Определить также  средние времена эксплуатации нерезервированной и резервированных систем.

   Решение. Функция надежности нерезервированной системы составляет

P^н/р(t)=(0,8)⁶=0.262. Определим требуемые числа резервных цепочек из выражений:

                P_A(t)=1-(1-P₁⁶(t))^s=0.95;                 P_B(t)=(1-(1-P₁(t))^s)⁶=0.95.      (1.2)

   Подставляя в выражения (1.2) P₁(10)=0.8 ,получим s_A=9.86, s_B=3.1. Соответственно,  принимаем s_A=10, s_B=4.

   Средние времена эксплуатации нерезервированной и резервированной систем при этом будут:

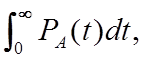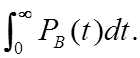        T_ср^н/р=1/6l₁,             T_ср^А=             T_ср^В=         (1.3)

   Интенсивность отказа единичного элемента l₁ определяется из условия

                    P₁(10)=   отсюда   l₁=0.023 1/час.

   Следовательно T_ср^н/р=7.25 часа. Способы вычисления интегралов (1.3) даны в п.1.1 пособия .В рассматриваемой задаче  T_ср^А=21.22 часа , T_ср^В=38.95 часа.