Методическое руководство к практическим занятиям по курсу "Основы математической теории надежности и её приложения к задачам электроэнергетики", страница 4

Номер	Расчетная	l , 1/год
варианта	схема	СШ	В	ВЛ	ОД	КЗ
15		0.06	0.03	0.50	0.02	0.02
Определить надежность электроснабжения нагрузок S1 и S2

 2. Надежность системы с зависимыми элементами

                               Типовые задачи с решениями

Предполагается, что система состоит из n одинаковых элементов , соединенных параллельно. Интенсивности отказов каждого из элементов системы не зависят от времени, но зависят от числа отказавших элементов. Так, например, если ограничитель перенапряжений скомплектован из n  параллельных колонок, то выход из строя колонки  варисторов приводит к перегрузке током остальных колонок и увеличению их интенсивности отказа.

   Среднее время эксплуатации такой системы при условии , что она выходит из строя при выходе из строя последнего элемента , определится как

             T_ср = 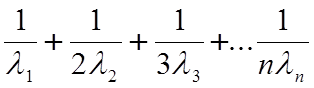.                              (2.1)

   Если же  отказ системы наступает , когда в ней остается m элементов, среднее время эксплуатации будет

              Т_ср(m) =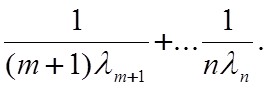                                                    (2.2)

   В выражениях (2.1) и (2.2)  _m ( m=1...n) - интенсивность отказа единичного элемента при эксплуатации в системе m элементов.

2.1 Система состоит из 4-х элементов, включенных в смысле надежности параллельно. Предполагая независимость элементов, определить среднее время эксплуатации системы при интенсивности отказа единичного элемента l = 1 1/год.

 Предполагая далее, что элементы зависимы , определитьинтенсивность отказа единичного элемента в системе из 4-х элементов (l₄), если интенсивности отказов обратно пропорциональны числу элементов, находящихся в эксплуатации, а  среднее время эксплуатации системы то же , что и для системы с независимыми элементами.

   Решение. Среднее время эксплуатации системы с независимыми элементами, включенными в смысле надежности параллельно, определяется как                                                          

                         Т_ср=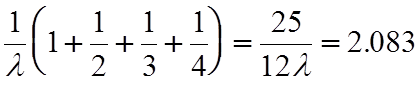 года.

   При эксплуатации системы с зависимыми элементами при заданном условии относительно интенсивности отказов элементов в неполной системе:

  l₃=l₄´4/3, l₂=l₄´4/2, l₁=l₄´4. Следовательно

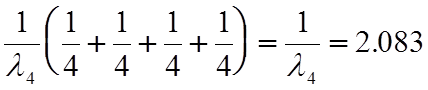                  Т_ср=года.

       и ₄=0.48 1/год.

2.2 Система состоит из 5 соединенных параллельно в смысле надежности элементов. Интенсивности отказов элементов обратно пропорциональны квадрату их количества в системе . Определить среднее время эксплуатации системы, если её отказ наступает в результате отказа трех элементов. Интенсивность отказа единичного элемента в полной системе составляет = 0.1 1/год.

   Решение. Если отказ системы наступает при отказе 3-х элементов , то m=2

( m  - число оставшихся в системе элементов к моменту её отказа).Следовательно, среднее время эксплуатации системы определится как

                                  Т_ср = 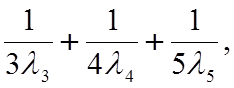                                       (2.3)        

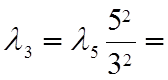где l₄=l₅₌0.1´1.5625=0.15625 1/год, 0.1´2.78=0.278.

   Подставляя l₃ ,l₄ и l₅ в (2.3),получим Т_ср= 4.8 года.

           Задачи для самостоятельного решения по разделу 2

                                   Задание 2

Задача 1. Варианты 1...6. Система состоит из n элементов, соединенных в смысле надежности параллельно. Отказ системы наступает после отказа всех её элементов. Интенсивность отказа элементов при их эксплуатации в полной системе - l_n. Задано соотношение между интенсивностями отказов элементов при их эксплуатации в системе из любого числа элементов m (m=1...n). Определить среднее время эксплуатации системы (Т_ср.зав.) и сравнить это время со средним временем эксплуатации системы с независимыми элементами (l=l_n).

№ варианта	n	ln, 1/год	lm , 1/год ( m= 1...n )
1	3	0.5	Обратно пропорциональна кубу числа
2	3	0.4	элементов, находящихся в эксплуатации
3	4	0.4	Обратно пропорциональна квадрату числа
4	4	0.3	элементов, находящихся в эксплуатации
5	5	0.3	Обратно пропорциональна квадратному
6	5	0.2	корню из числа элементов, находящихся
			в эксплуатации

   Варианты 7...12. Система состоит из n элементов, соединенных в смысле надежности параллельно. Отказ системы наступает после отказа всех её элементов. Определить среднее время эксплуатации системы с независимыми элементами при интенсивности отказа единичного элемента

l=0.1 1/год, а также интенсивность отказа единичного элемента в полной системе с зависимыми элементами ( l_n ) , при которой средние времена эксплуатации системы с независимыми и зависимыми элементами будут одинаковы. Соотношение между интенсивностями отказов элементов в системе с зависимыми элементами при любом их числе  задано.

№ варианта	n	lm , 1/год  (m = 1...n )
7	3	Обратно пропорциональна четвертой степени  числа
8	5	элементов, находящихся в эксплуатации
9	3	Обратно пропорциональна квадратному корню из
10	4	числа элементов, находящихся в эксплуатации
11	4	Обратно пропорциональна кубу числа элементов ,
12	5	находящихся в эксплуатации