Методическое руководство к практическим занятиям по курсу "Основы математической теории надежности и её приложения к задачам электроэнергетики", страница 9

P^**(t)=1-Q^**(t)=1-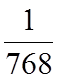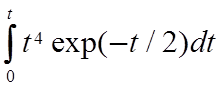=exp(-t/2)(t⁴/16+t³/2+3t²+12t+24) (5.11)

   Интенсивность потока отказов l^**(t) при этом будет

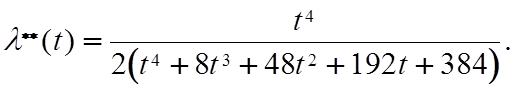                                          (5.12)

    Полная интенсивность потока отказов рассматриваемого элемента определится следующим образом:

                            l(t)=0.5+l**(t).                                                            (5.13)

   Результаты расчетов l(t) сведены в таблицу .

t, год	0	1	2	3	4	5	6	7	8	9
l,1/год	0.500	0.500	0.508	0.524	0.548	0.575	0.603	0.630	0.655	0.678
t, год	10	20	30	40	50	60	70	80	90	100
l,1/год	0.699	0.823	0.877	0.906	0.923	0.936	0.945	0.951	0.957	0.961

   Из таблицы  видно, что примерно до 3-4 лет эксплуатации элемента наибольший вклад в интенсивность его отказов вносят так называемые случайные отказы, характеризуемые постоянной интенсивностью , а затем все больший удельный вес приобретают отказы,обусловленные старением

элемента.

                 Задачи для самостоятельного решения по разделу 5

                                             Задание 5

   Во всех вариантах пятого задания следует получить зависимость интенсивности потока отказов стареющего элемента от времени его эксплуатации.

№ варианта	q(t)	Параметры закона
1	Г-распределение	1 час
2		,    1 час
3	Закон Релея
4
5	Закон Вейбулла	,   c= 1 1/час3
6		,   с= 1 1/час2
	- распределение
7		n=4

        -

№ варианта	q	Параметры закона
8	- распределение	n=2
9		n=3
	Закон Максвелла
10		= 1 год
11	Законы экспоненциальный и	l*=3 1/год,
	Максвелла	=1 год
12	Законы экспоненциальный и	l*=0.3 1/год
	Г-распределение	a=3 ,  b= 1 год
13	Законы экспоненциальный и	l* = 1 1/год
	Релея	= 1 1/год
14	Законы экспоненциальный и	l*= 1 1/год
	Вейбулла	a= 1,   с= 1 1/час3
15	Законы экспоненциальный и	l*=0.3 1/год
	c2 - распределение	n=6

 6. Предупредительные замены стареющих элементов

                     Типовая задача с решением

 Стареющие элементы часто целесообразно заменять , не дожидаясь выхода их из строя. Если элемент является составной частью какой-либо системы , то такая плановая его замена может существенно повысить надежность эксплуатации системы в целом .Следовательно, замены стареющего элемента происходят либо через некоторое заранее установленное время t_пл, либо в результате его внезапного отказа .

   Эффективность такого способа эксплуатации стареющего элемента может быть оценена путем сравнения математических ожиданий времен эксплуатации элемента при отсутствии его плановых замен и при некотором их числе n.

   Среднее время эксплуатации элемента при его n предупредительных заменах определяется как

             .     (6.1)

   В выражении (6.1) применены следующие обозначения

                  - плановый срок замены стареющего элемента,

               - значение функции надежности при  ,

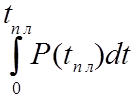             = - среднее время эксплуатации элемента при

                                                плановой его замене ,                                (6.2)

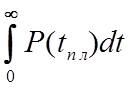               =   - среднее время эксплуатации элемента при

                                            отсутствии замен.                                           (6.3)

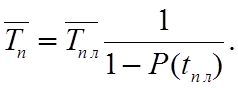    При       n           lim                                       (6.4)

   Определим средние времена  ,  ,  и lim  при n эксплуатации элемента, функция надежности которого подчинена усеченному нормальному закону с параметрами  s₀= 1 год , t₀= 2 года, а плановые сроки замен отвечают P(t_пл) = 0.2 и 0.5.

 Решение.  В  рассматриваемом случае t_пл определяется из  выражения (2.5):

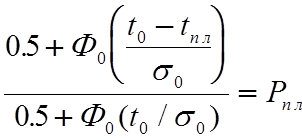                            .                                           (6.5)

   Если обозначить 0.5+, то

                            t_пл=t₀-arcF₀(b₀P_пл - 0.5)´s₀ .                                         (6.6)

   При принятых параметрах усеченного нормального закона t_пл=2.028 года при P_пл=0.5 и t_пл=2.858 года при Р_пл=0.2.

   Математические ожидания времени эксплуатации элемента при заменах его через плановые сроки () и при отсутствии таких замен () при полученных значениях интервалов времени между плановыми заменами определятся как :

           года ,                года,

          =2.06 года.