Математика \ Основы математической теории надежности и её приложения к задачам электроэнергетики

Методическое руководство к практическим занятиям по курсу "Основы математической теории надежности и её приложения к задачам электроэнергетики", страница 5

  Варианты 12...15. Система состоит из n элементов, соединенных в смысле надежности параллельно. Отказ системы наступает после отказа всех её элементов. Определить среднее время эксплуатации системы с зависимыми элементами , если ln=0.1 1/год, а интенсивности отказов единичных элементов в неполной системе обратно пропорциональны квадрату числа эксплуатируемых элементов. Найти также интенсивность отказа l единичного элемента в системе с независимыми элементами, при которой средние времена эксплуатации в системах с зависимыми и независимыми элементами будут одинаковыми.

№ варианта

            13

           14

           15

           n                          

             4

            5

            6

   Задача 2. Во всех вариантах определить в условиях первой задачи среднее время эксплуатации системы с зависимыми элементами , выходящей из строя  при отказе q элементов.

№ вар.

 1

 2

 3

 4

 5

 6

 7

 8

 9

10

11

12

13

14

15

     q

 2

 2

 2

 2

 3

 3

 1

 2

 2

 3

 3

 4

 2

 2

 3

           3. Надежность восстанавливаемого элемента

                Типовые задачи с решениями

3.1 Время восстановления элемента пренебрежимо мало.

   Примем далее , что поток отказов элемента является простейшим потоком , т.е. потоком Пуассона . Вероятность того,что за время t произойдет ровно к отказов, в этом случае определяется как

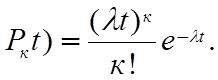                                                                          (3.1)

   Вероятность того, что за время t число отказов превысит n ,будет

               P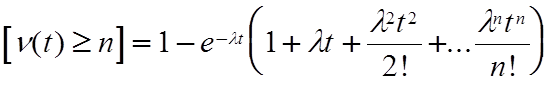.          (3.2)

   При достаточно большом значении n ряд, входящий в (3.2), может быть при использовании центральной предельной теоремы Ляпунова просуммирован:

              P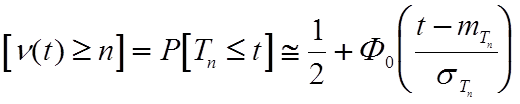,                (3.3)

где 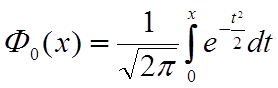   - функция Лапласа,

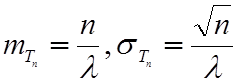       - математическое ожидание и среднеквадратическое отклонение времени наступления n-го отказа (Тn.).

       3.1.1 Элемент эксплуатируется с заменами при пренебрежимо малом времени его восстановления. Какое число запасных элементов необходимо иметь, чтобы их хватило на эксплуатацию в течение года с вероятностями 0.90 , 0.95 и 0.99 ? Интенсивность потока отказов элемента l = 5 1/год.

        Решение . Применим для решения асимптотическое выражение (3.3).Для надежной эксплуатации элемента необходимо, чтобы число запасных элементов n  отвечало бы условию где Р = 0.90;0.95 и 0.99. Следовательно

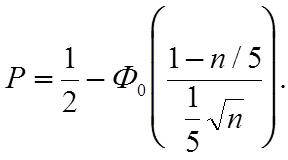        и  .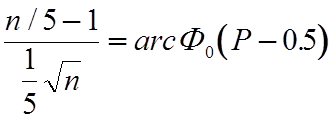

     Из последнего выражения получаем n »9 , »11 и » 14  при Р=0.90; 0.95 и 0.99 , соответственно.

3.1.2 Элемент эксплуатируется с заменами при пренебрежимо малом времени его восстановления.Какова должна быть интенсивность отказа единичного элемента, чтобы при его эксплуатации в течение  года потребовалось бы с вероятностью не менее 0.95 не более трех замен?

     Решение. В рассматриваемой задаче из-за малого значения  n нельзя воспользоваться асимптотическим выражением (3.3). Поэтому согласно (3.2) будем иметь:

                      (3.4)

   Или при t=1год и при замене знака неравенства знаком равенства выражение (3.4) запишется в виде

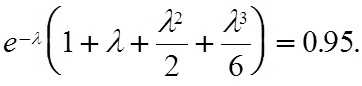                                                           (3.5)

   Решая трансцендентное уравнение (3.5) каким-либо численным методом, получим  l= 1.36 1/год.

3.2. Время восстановления элемента соизмеримо со временем его эксплуатации до отказа .

   Одной из основных характеристик этого процесса является коэффициент готовности КГ(t) , т.е. вероятность того, что в момент времени t  элемент находится в исправном состоянии. В случае, если потоки отказов и восстановлений являются потоками Пуассона и рассматривается стационарный режим эксплуатации

                                КГ=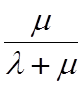,                                                               (3.6)

   где  l и m - интенсивности потоков отказов и восстановлений элемента .

   Вводится также понятие наработки на отказ Тt в течение времени эксплуатации элемента t. При Пуассоновских потоках отказов и восстановлений закон распределения суммарной наработки на отказ асимтотически нормален , причем М[Tt]=KГ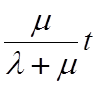t =, D[Tt] =

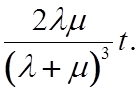
   Можно оценить доверительный интервал для времени наработки на отказ при некоторой доверительной вероятности Рд:

              Рд= Р(t1£Tt£t2)= F0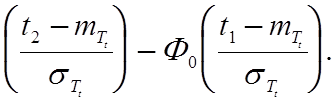                                  (3.7)

3.2.1. Элемент эксплуатируется с заменами при конечном времени его восстановления. Интенсивности потоков отказов и восстановлений составляют l= 0.5 1/час и m= 0.2 1/час.Математическое ожидание времени наработки на отказ за время t составляет М[Tt]=600 часов.Определить вероятность того, что время наработки на отказ будет находиться в диапазоне 550...650 часов.

       Решение. Суммарное время эксплуатации элемента определится как

                              t=M[Tt]´(l+m)/l=600´0.7/0.2=2100 часов.

   Следовательно, дисперсия времени наработки на отказ будет

        D[Tt]=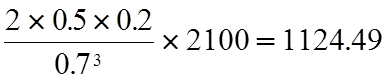час2  и s[Tt]=35 часов.

   Вероятность того,что время наработки на отказ будет находиться в диапазоне 550...650 часов ,определится как

                  Pд=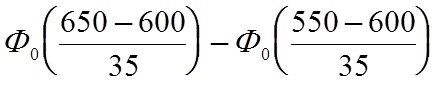=0.8468.

3.2.2. Элемент эксплуатируется с заменами при конечном времени его восстановления. Интенсивность потока его отказов l=2 1/час, КГ=0.4. Определить суммарное время эксплуатации элемента  t , если доверительный интервал для времени наработки на отказ  при Рд=0.90 составляет 250 часов ?

       Решение. По заданным коэффициенте готовности КГ и интенсивности потока отказов l определим интенсивность потока восстановлений m:

                                    0.4=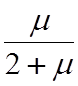  , откуда m=1.33(3).

Скачать файл