В варианте 13 при заданных интенсивностях потоков отказов l=m= 1 1/час определить суммарное время эксплуатации t и математическое ожидание времени наработки на отказ M[Tt] , если доверительный интервал Tt при доверительной вероятности Рд=0.997 ( вокруг M[Tt]) составляет 120 часов.
В варианте 14 при заданных интенсивности потока отказов l=0.8 1/час, суммарном времени эксплуатации элемента t = 1300 часов и математическом ожидании времени наработки на отказ M[Tt]= 800 часов определить интенсивность потока восстановления элемента m , а также доверительную вероятность попадания Tt в интервал 800...1000 часов.
В варианте 15 при заданных интенсивностях потоков отказов l= 5 1/час , восстановлений m= 1 1/час и математическом ожидании времени наработки на отказ M[Tt] = 600 часов определить суммарное время эксплуатации элемента t , а также доверительный интервал для времени наработки на отказ
( вокруг M[Tt] ), отвечающий Рд=0.99.
4. Резервирование в технических системах
Типовая задача с решением
Резервирование является одним из способов повышения надежности технических систем. Обычно рассматриваются следующие виды резерва:
n нагруженный или горячий резерв,
n ненагруженный или холодный резерв,
n облегченный резерв.
Возможная схема эксплуатации системы с резервированием приведена на рис.4.1. Каждый отказавший элемент поступает в ремонтное устройство, содержащее r ремонтных единиц, каждая из которых может мгновенно восстанавливать один элемент. Если все ремонтные места заняты, то элемент ставится в очередь.Система эксплуатируется исправно, если число рабочих элементов не меньше j (j£ n ).
Нагруженный 
Рабочие
резерв элементы
( m ) ( n )
Облегченный
Ремонтное
резерв 
устройство
( 
)
( r )
 |
Ненагруженный
резерв
( s )
Рис.4.1 Схема эксплуатации системы с резервированием
Вероятность того, что система находится в состоянии к ( в системе отказало к элементов ), определяется как
pk=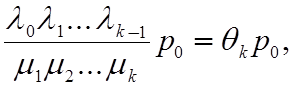
где к=1...(N-j) . (4.1)
Входящая в выражение (4.1) вероятность р0 определяется следующим образом
, 
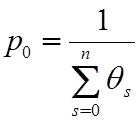(4.2)
Интенсивности отказа и восстановления системы , находящейся в к-ом состоянии , определяются по выражениям:
(n+m)
при
0£ к £ s,
= (n+m)l +
при s £ k £s+
(4.3)
(n+m+
при s+
k
при 
mk = (4.4)
при
> r .
4.1. В системе эксплуатируется 4 рабочих элемента(n=4),
2 элемента; находящихся в горячем резерве (m=2) и 1
элемент - в облегченном резерве(
.
Интенсивности отказов элементов , находящихся в рабочем режиме и в режиме
нагруженного горячего резерва , составляют l=0.5
1/час , в режиме облегченного резерва =0.25
1/час.Число ремонтных единиц r=2. Интенсивность потока
восстановления m=1 1/час.
Определить вероятности эксплуатации системы при к отказавших элементах ,
математическое ожидание числа отказавших элементов , а также вероятность
сохранения работоспособности системы ( система выполняет свои функции, если в
ней эксплуатируется не менее трех рабочих элементов ). Сравнить полученные
результаты с результатами в системе , содержащей 4 ремонтных единицы ( r=4).
Решение. Интенсивности
потоков отказов системы, находящейся в к-м состоянии, будут: l0=(4+2)l+=3.25 1 1/час, 
В случае 2-х ремонтных единиц
интенсивности потоков восстановления системы, находящейся в к-м состоянии ,
определятся как 
1/час, mк=2m
( к=2...7).
Вероятности эксплуатации системы при к отказавших элементов согласно (4.1) и (4.2) будут: р0=3.41647´10-2, р1=1.1088158´10-1, р2=1.6632238´10-1,
р3=р4=2.0790297´10-1, р5=1.5592723´10-1, р6=7.79963514´10-2, р7=3.8901808´10-2. Математическое ожидание
числа отказавших элементов составляет М[k]=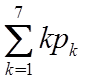
=3.419.Вероятность сохранения работоспособности системы
отвечает эксплуатации не менее 3-х элементов: Р=р0+р1+р2+р3+р4=0.727.
В случае, если число ремонтных
единиц составляет r=4, интенсивности потоков
восстановления будут: 
(к=1...4), m5=4!´4, m6=4!´42,m7=4!´43. При этом вероятности рк
определятся как: р0=0.0640504,р1=2.0816367´10-1, р2=3.122455´10-1, р3=2.6020459´10-1, р4=1.3010229´10-1, р5=9.9871956´10-3,
р6=1.219709´10-2,р7=3.0492725´10-3. При этих значениях вероятностей pk
M[k]=2.278 , P=p0+p1+p2+p3+p4=0.975.
Таким образом, увеличение числа ремонтных единиц с 2-х до 4-х привело к уменьшению математического ожидания числа отказавших элементов с 3.419 до 2.278 и к увеличению вероятности сохранения работоспособности системы с 0.727 до 0.975.
Задачи для самостоятельного решения по разделу 4
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.