Методическое руководство к практическим занятиям по курсу "Основы математической теории надежности и её приложения к задачам электроэнергетики", страница 6

При нормальном законе распределения =2F₀(k).

   Cледовательно, при Р_д=0.9  F₀(к)=0.45 и к=1.645. По заданию 1.645s=125 часов , s[T_t]=76 часов и D[T_t]=5776 час². Суммарное время эксплуатации элемента определится  из выражения

                  5776=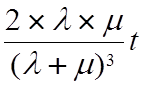. Отсюда t=40111часов.

   Математическое ожидание времени наработки на отказ составит

                 M[T_t]=K_Г´t=0.4´40111=16044 часа.

                 Задачи для самостоятельного решения по разделу 3

                                                   Задание 3

Задача 1. Варианты 1 и 2. Элемент эксплуатируется с заменами при пренебрежимо малом времени его восстановления. Интенсивность потока отказов l=5 1/год. Сколько должно быть запасных элементов (n) , чтобы с вероятностью не менее Р элемент эксплуатировался бы в течение t лет?

Номер варианта	Р	t ,  года
1	0.90,    0.95 ,    0.99	3
2	0.90,    0.95,     0.99	1

  Варианты 3...6. Элемент эксплуатируется с заменами при пренебрежимо малом времени его восстановления. Интенсивность потока отказов  -l. Определить время , при котором с вероятностью Р произойдет не более n замен.

Номер варианта	l ,  1/год	Р	n
3	0.5	0.95	3
4	10	0.90	100
5	5	0.95	50
6	3	0.90	30

   Варианты 7...12. Элемент эксплуатируется с заменами при пренебрежимо малом времени его восстановления. Какова должна быть интенсивность потока отказов элемента в год, чтобы при его эксплуатации в течение времени t потребовалось бы с вероятностью не менее Р не более n замен?

Номер варианта	t , года	Р	n
7	2	0.90	4
8	10	0.95	100
9	1	0.95	2
10	5	0.90	50
11	2	0.95	50
12	3	0.90	100

   Варианты 13...15. Элемент эксплуатируется с заменами при пренебрежимо малом времени его восстановления. Имеется n запасных элементов с интенсивностью потока отказов l. Какова вероятность, что этих элементов достаточно для эксплуатации в течение t лет?

Номер варианта	n	l ,  1/год	t ,  года
13	3	0.5	2.5
14	50	5	10
15	100	10	10

   Задача 2.Варианты 1...6. Элемент эксплуатируется с заменами при конечном времени его восстановления. Заданы: интенсивности потоков отказов (l) и восстановлений (m) , математическое ожидание времени наработки на отказ M[T_t] . Определить вероятность Р_д попадания T_t  некоторый диапазон T_t.

Номер варианта	l , 1/час	m , 1/час	M[Tt] , час	Tt , час
1	0.2	0.3	600	550...650
2	4	4	800	800...830
3	0.3	0.1	500	300...600
4	0.5	0.8	800	M[Tt]
5	0.3	0.2	500	M[Tt]
6	0.2	0.3	600	M[Tt]

   Варианты 7 и 8. Элемент эксплуатируется с заменами при конечном времени его восстановления. Заданы: суммарное время его эксплуатации t, интенсивности потоков отказов(l) и восстановлений (m). Определить вероятность того , что время наработки на отказ (T_t) окажется в диапазоне

T_t  часов.

Номер варианта	l , 1/час	m , 1/час	t , час	Tt , час
7	0.1	0.2	3000	2000...2800
8	0.2	0.3	1000	500... 700

   Варианты 9 и 10.  Элемент эксплуатируется с заменами при конечном времени его восстановления. Заданы: суммарное время его эксплуатации t, интенсивности потоков отказов (l) и восстановлений (m). Определить интервал времени наработки на отказ M[T_t], отвечающий доверительной вероятности Р_д.

Номер варианта	l , 1/час	m , 1/час	t , 1/ час	Рд
9	0.2	0.3	1000	0.95
10	0.1	0.2	3000	0.90

   В варианте 11 при заданных коэффициенте готовности К_Г=1/3 , интенсивности потока отказов l= 1 1/час и доверительном интервале для времени наработки на отказ 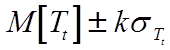= 200 часов при Р_д=0.95 определить суммарное время эксплуатации элемента t .

   В варианте 12  при заданных интенсивностях потоков l=0.2 1/час , m=0.3 1/час  и дисперсии времени наработки на отказ D[T_t]=960 час² определить суммарное время эксплуатации элемента  t  и диапазон времени наработки на отказ T_t ( вокруг M[T_t] ), отвечающий доверительной вероятности Р_д= 0.90.