Методическое руководство к практическим занятиям по курсу "Основы математической теории надежности и её приложения к задачам электроэнергетики", страница 11

    Срок службы аппарата определится из уравнения(7.4):

                    0.5-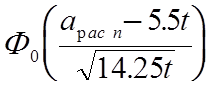=0.95.

   Отсюда  _расп-5.5t=3.586.Подставляя _расп=106, получим квадратное уравнение для определения срока службы t:

                             x² - 1.129x - 19.27=0  ( x =).

   Решив уравнение , получим t=25 лет. Следует отметить, что такой срок службы аппарата на уровне надежности 0.95 вполне приемлем.

7.2. Защитный аппарат среднего класса напряжения состоит из 5 последовательно соединенных варисторов (s=5). Разрушающий ток генеральной совокупности элементов распределен по нормальному закону с параметрами M[I_р]=400 A , s[I_р]=90 A.  Сравнить функции распределения разрушающего тока для генеральной совокупности варисторов и для наиболее " слабого" элемента из этой совокупности. Определить также математическое ожидание и среднеквадратическое отклонение разрушающего тока для наиболее "слабого" варистора.

   Решение. Согласно (7.8) функция распределения разрушающего тока наиболее "слабого" варистора из 5 запишется в виде:

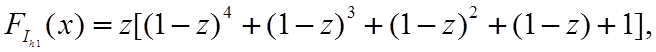                  ( 7.10)

     где 

                          z=0.5+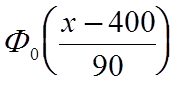- функция распределения разрушающего тока совокупности из пяти единичных варисторов .

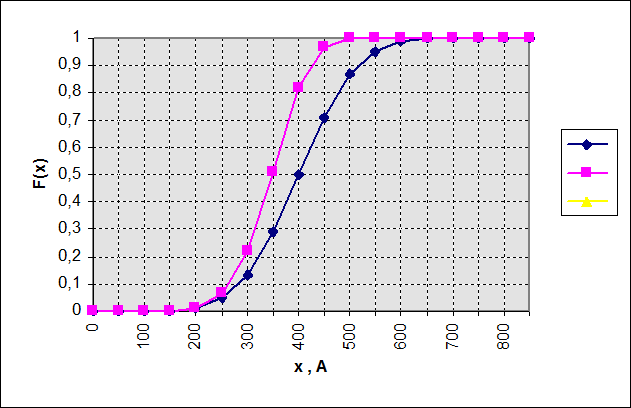
      Результаты расчетов приведены на рисунке, на котором указаны расчетные точки. Правая кривая отвечает  функции распределения разрушающего тока совокупности из пяти варисторов , левая - наиболее "слабому "варистору из пяти.

                           

   Математическое ожидание ожидание и среднеквадратическое отклонение разрушающего тока наиболее "слабого" варистора из генеральной совокупности определяются как

    M[I_p1] = 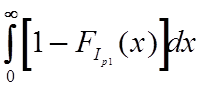  ,   D[I_p1] = 2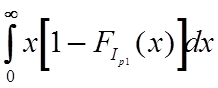-M²[I_p1].        (7.11)

   В рассматриваемом примере , вычисляя интегралы (7.11) численно, получаем M[I_p1]=295 A ,  D[I_p1]=61.8 A.

              Задачи для самостоятельного решения по разделу 7

                                                Задание 7

    Варианты 1...12. Токовые воздействия на ОПН  определяются, в основном, двумя коммутациями, для которых заданы  числовые характеристики расходуемого ресурса (во всех вариантах принять s[А_расх1j]=2M[А_расх1j], j =1,2). Интенсивности потоков этих коммутаций составляют l₁=5 1/год , l₂=10 1/год.

   В вариантах 1...6 определить величину требуемого располагаемого ресурса аппарата , при которой срок службы ОПН на уровне надежности 0.95 составляет 25 лет ( F_T(25) = 0.95).

   В вариантах 7...12 при заданном значении располагаемого ресурса определить срок службы аппарата на уровне надежности 0.95.

Характеристики	Номер варианта
расход. ресурса	1 , 7	2 , 8	3 , 9	4 , 10	5 , 11	6 , 12
М[Aрасх11]	0.7	0.6	0.5	0.7	0.6	0.5
M[Aрасх12]	0.1	0.1	0.05	0.05	0.2	0.1
арасп	83	74	54	71	98	66

             Примечание: а_расп задано в вариантах  7...12.

   В вариантах  13...15  построить функции распределения разрушающего тока аппарата с параметрами варисторов,отвечающими их генеральной совокупности объемом s, и c параметрами наиболее "слабого" варистора из

этой генеральной совокупности.

   Заданы числовые характеристики разрушающего тока с параметрами варисторов , отвечающими генеральной совокупности.

   Определить также математическое ожидание и среднеквадратическое отклонение разрушающего тока наиболее "слабого" варистора.

Номер варианта	M[Iр] , A	s[Ip] , A	s
13	300	90	4
14	300	90	5
15	500	100	5

                                              Литература

   1.Кадомская К.П. Основы математической теории надежности и её приложения к задачам электроэнергетики: Учебное пособие/Новосиб.гос.техн.ун-т.-Новосибирск.-1995.-68 с.

     Кадомская К.П. Основы математической теории надежности и её приложения к задачам электроэнергетики: Сборник задач/Новосиб.гос.техн. ун-т.-Новосибирск-1998.-       с.

   В сборнике рассматриваются способы решения задач из некоторых разделов математической теории надежности и её приложений к задачам электроэнергетики.По каждому разделу даны типовые задачи с подробными их решениями и приводятся задачи для самостоятельного их решения студентами.

         Рецензент канд.техн. наук , доцент

                         И.А. Ефремов

   Работа подготовлена кафедрой техники и электрофизики высоких

                                             напряжений

                                                                     Новосибирский государственный

                                                                     технический университет,1998 г.

                                           Редактор И.Л.Кескевич

                                          Корректор

621

                                                К.П.КАДОМСКАЯ

ОСНОВЫ МАТЕМАТИЧЕСКОЙ

                                   ТЕОРИИ НАДЕЖНОСТИ

                                      И ЕЕ ПРИЛОЖЕНИЯ

                         К ЗАДАЧАМ ЭЛЕКТРОЭНЕРГЕТИКИ

                                              Сборник задач

                        

                                             Новосибирск

                                                     1998