Методическое руководство к практическим занятиям по курсу "Основы математической теории надежности и её приложения к задачам электроэнергетики", страница 8

В системе эксплуатируется 3 рабочих элемента (n=3), один - в нагруженном резерве ( m=1)  и один в ненагруженном резерве (=1). Интенсивности потоков отказов составляют 2 1/час , = 1 1/час. Остальные характеристики надежности системы заданы в таблице. Определить вероятности эксплуатации системы при к отказавших элементах , математическое ожидание числа этих элементов M[k] , а также вероятность сохранения работоспособности системы Р (система работоспособна, если число рабочих элементов не меньше j).

Номер варианта	m, 1 1/час	r	j
1		1	3
2		2	2
3	1	3	1
4		4	3
5		5	2
6		1	3
7		2	2
8	2	3	1
9		4	3
10		5	2
11		1	3
12		2	2
13	3	3	1
14		4	3
15		5	2

5. Законы распределения сроков службы стареющих

                                 элементов

                              Типовые задачи с решениями

   В предыдущих заданиях в качестве закона надежности принимался экспоненциальный закон , характеризующийся независимостью интенсивности отказа элементов от времени. Вместе с тем некоторые элементы стареют, начиная с некоторого срока их эксплуатации , а иногда с момента  начала эксплуатации. Интенсивность отказа таких элементов возрастает во времени . При известном законе надежности интенсивность отказа элемента определится как

                                         l(t)=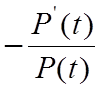.                                         (5.1)

   5.1.Усеченный нормальный закон. Поскольку срок службы любого технического  изделия Т³ 0, то в качестве закона надежности стареющего элемента может быть принят, в частности, нормальный закон, усеченный слева:

                                  P(t)=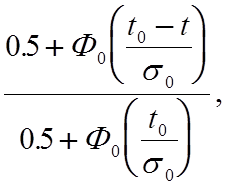                                       (5.2)

   Входящие в (5.2) параметры  и  связаны с математическим ожиданием и дисперсией срока службы Т следующими соотношениями:

                                 M[T] = t₀+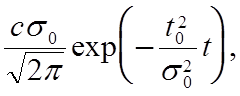                               (5.3)

                            D[T] = 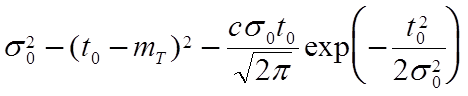.        (5.4)

   В выражениях (5.3) и (5.4) 

                             c=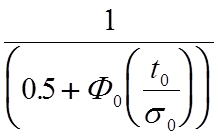-  коэффициент усечения.

   Производная от Р(t) ,будет

                                  P^'(t) = 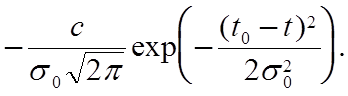                   (5.5)

   Следовательно , зависимость интенсивности отказов от времени при усеченном нормальном законе распределения определяется по выражению:

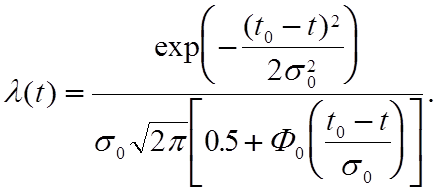                                                   (5.6)

   Задан параметр s₀= 1 год. Построить зависимость l(t) при t₀= 1, 2 и 5 лет.

Решение. Результаты расчетов по выражению (5.6) приведены в таблице 5.1.

   Из таблицы следует достаточно очевидный вывод: с увеличением параметра t₀, связанного с математическим ожиданием срока службы с помощью выражения (5.3), рост интенсивности потока отказов со временем уменьшается.

                                                                                                 Таблица 5.1

        Зависимость интенсивности потока отказов стареющего  элемента при

        функции надежности , подчиненной  усеченному нормальному закону

t0	t ,  года
года	0	1	2	3	4	5	6	7	8	9
1	0.288	0.798	1.525	2.373	3.283	4.226	5.186	6.158	7.138	8.274
2	0.055	0.288	0.798	1.525	2.373	3.283	4.226	5.186	6.158	7.138
5	0.000	0.000	0.004	0.055	0.288	0.798	1.525	2.373	3.283	4.226

5.2. Комбинированный закон. В ряде случаев функция надежности стареющего элемента может быть описана комбинированным законом :

                                      Р(t)=P^*(t)´P^**(t).                                          (5.7)

     При этом интенсивность отказа элемента определится как

                                     l(t)=l^*(t)+ l^**(t),                                           (5.8)

   где

                l^*(t) = 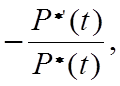       l^**(t) = 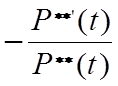.                           (5.9)

    Пусть функция надежности некоторого элемента описывается комбинацией  экспоненциального закона  и Г-распределения:

                  q^*(t)=l^*exp(-l^*t)  ,  q^**(t) = 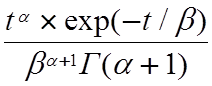,                 (5.10)

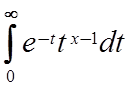
                       где Г(х) = - гамма-функция .   

   Определим зависимость интенсивности потока отказов от времени при следующих параметрах Р^*(t) и Р^**(t) : l^*=0.5 1/год , a=4 , b= 2 года.

   Функция надежности, отвечающая частости потока отказов (5.10), при принятых параметрах Г-распределения определится как