Формула полной вероятности и вычисление вероятности события. Ковариация двух случайных величин

Министерство Российской Федерации по связи и информатизации

Сибирский Государственный Университет Телекоммуникаций и Информатики

Межрегиональный центр переподготовки специалистов

ОТЧЕТ

по курсовой работе

«Теория вероятностей и математическая статистика»

Вариант № 6

2011

Часть I: Теория вероятностей и математическая статистика

Задача 1.

В партии из N деталей ровно M бракованных. Дайте ответы на следующие вопросы (запишите формулы и сделайте вычисления с подробными объяснениями):

а) какова вероятность того, что наудачу выбранная деталь из партии окажется бракованной?

б) какова вероятность того, что наудачу выбранная деталь из партии окажется НЕ бракованной?

в) какова вероятность того, что из K₁ случайно выбранных из партии деталей ровно L₁ окажется бракованными?

г) какова вероятность того, что из K₂ случайно выбранных из партии деталей не более L₂ окажется бракованными?

д) какова вероятность того, что из K₃ случайно выбранных из партии деталей не менее L₃ окажется НЕ бракованными?

е) из партии выбрано случайно K₄ деталей, из них L₄ оказалось бракованными; какова вероятность, что больше в выборке нет бракованных деталей?

ж) из партии выбрано K₅ деталей, и которых не менее L₅ оказалось бракованными; какова вероятность того, что в последующей выборке из K₆ деталей бракованных окажется не более L₆ (предыдущая выборка в партию не возвращается)?

Числовые данные

N=140000, M=10920, K1=1097, L1=39, K2=1000, L2=10, K3=1107, L3=5, K4=517, L4=67, K5=917, L5=13, K6=423, L6=11

Решение:

a) Из N деталей можно выбрать один N способами, а один бракованный M способами, следовательно  P=M/N=0.078.

б) Тут имеем событие, противоположенное событию из пункта а), => p=1-M/N=(N-M)/N=0.922.

в) Ясно, что если  L1 > M, то невозможно, чтобы из K1 случайно выбранных деталей ровно L1 вышло бракованными. Пусть    Из N деталей можно выбрать   способами.

L1 бракованные детали надо выбрать из M, а остальные   K1-L1  небракованные из  N-M не бракованных. Количество выборов в 1-ом случае  равно   , во втором случае   =>

По принцыпу умножения  получим число выборов, в которых ровно L1  бракованные:

г) Если   то ясно что в любой выборке не более M => не более L₂ элементов не бракованные.  Пусть  L₂ < M. Из N элементов можно выбрать  K₂,     способами. Пусть

  любое целое число. Пусть X – число бракованных элементов среди выбранных K₂. Найдем   Из M бракованных элементов можно выбрать  способами, из N-M  не бракованных можно выбрать остальные   способами  =>  по принцыпу умножения получим:

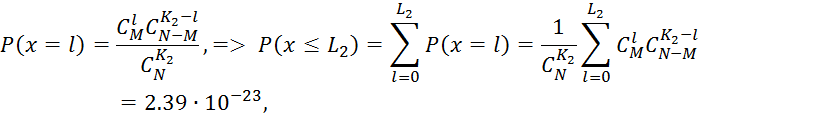
д)  Если   

 Аналогично получим:

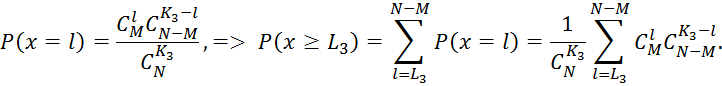
е) Тут речь идет о условной вероятности  Аналогично пункта д) и используя формулу Байеса, получим:

.

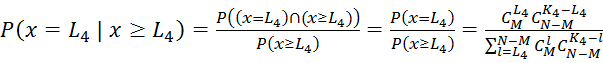ж) В данной задаче проведено два эксперимента:

I. Выбрали  деталей из N;

II. Выбрали  деталей из .

У первого эксперимента может быть  исхода. Результаты второго эксперимента зависят от результатов первого.

Вероятность в первом эксперименте выбрать одну бракованную деталь равна . Пусть в первом эксперименте выбрали s бракованных деталей, . Вероятность выбрать s бракованных деталей в первом эксперименте (обозначим это событие ) можно вычислить по формуле Бернулли:  , где . События  составляют полную группу событий.

После проведения первого эксперимента в партии осталось  деталей, из них  бракованных. Вероятность выбрать одну бракованную деталь во втором эксперименте равна . Вероятность выбрать во втором эксперименте r бракованных деталей при условии, что в первом эксперименте их было s штук, равна , .  Вероятность выбрать во втором эксперименте от 0 до () бракованных деталей при условии  можно вычислить как сумму вероятностей событий {выбрали r бракованных деталей}, , то есть по формуле . Далее по формуле полной вероятности вычисляем вероятность события {выбрали от 0 до  бракованных деталей}:

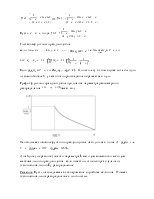
. Результат получен с помощью программы в математическом пакете Maple:

> P:=0:PHss:=0:for s from 13 to 917 do

PHs:=binomial(K5, s)*p^s*q^(K5-s); #P(H_s)

p_s:=(M-s)/(N-K5);  q_s:=1-p_s;   P:=P+PHs*sum(binomial(K6, r)*p_s^r*q_s^(K6-r) , r=0..L6);# прибавляем P(H_s)*P(L_6|s) od:

Задача 2.

«Неправильную» монетку (вероятность выпадения «орла» составляет A) подбрасывают N раз. Рассматриваются следующие величины: x — количество выпавших «орлов», y — количество выпавших «решек», , , . Ответьте на следующие вопросы об этих случайных величинах:

а) опишите распределения с.в. x, y, z₁, z₂, z₃; найдите математические ожидания, вторые моменты, дисперсии;

б) опишите условное распределение с.в. x|y;

в) в процессе подбрасывания на M-том броске оказалось, что уже выпало ровно L «орлов», какова вероятность того, что всего выпадет не более K решек?

г) найдите ковариацию и коэффициент корреляции величин x и y;

д) найдите ковариацию и коэффициент корреляции величин x² и y;

Числовые данные

A=0,69; N=252; M=142; L=80; K=55

Решение а) опишите распределения с.в. x, y, z₁, z₂, z₃; найдите математические ожидания, вторые моменты, дисперсии;