Формула полной вероятности и вычисление вероятности события. Ковариация двух случайных величин, страница 5

Найдем по таблице критических точек распределения по уровню значимости  и числу степеней свободы критическую точку правосторонней критической области .

Так как наблюдаемое значение критерия значительно больше  критического значения критерия , то делаем вывод о том, что наблюдения не согласуются с экспоненциальным  распределением на уровне значимости .

В пункте д) была найдена оценка параметра .

Найдем плотность предполагаемого нормального распределения с парметрами 0,0295 и 1

,

Найдем теоретические частоты:

,

,

,

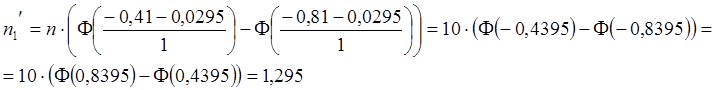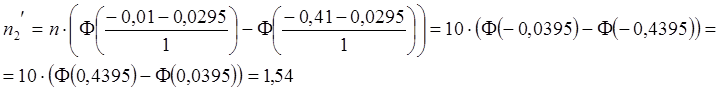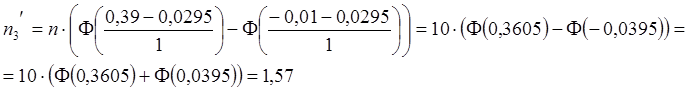Сравним эмпирические и теоретические частоты, используя критерий Пирсона

[-0,81;-0,41]	1	1,295	-0,295	0,16	0,067
[-0,41;-0,01]	3	1,54	1,46	2,1316	1,38
[-0,01;0,39]	1	1,57	-0,57	0,3249	0,21
[0,39;0,79]	4	1,36	2,64	6,9696	5,12
сумма	10

Найдем по таблице критических точек распределения по уровню значимости  и числу степеней свободы критическую точку правосторонней критической области .

Так как наблюдаемое значение критерия больше  критического значения критерия , то делаем вывод о том, что наблюдения не согласуются с нормальным  распределением с параметрами 0, 0295 и 1 на уровне значимости .

В пункте е) была найдена оценка параметра ,

Найдем плотность предполагаемого нормального распределения с парметрами 0,0295 и 0,48

,

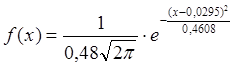Найдем теоретические частоты:

,

,

,

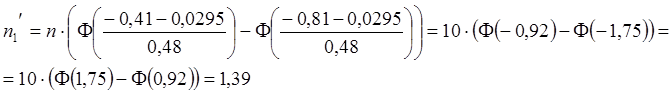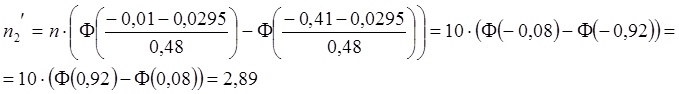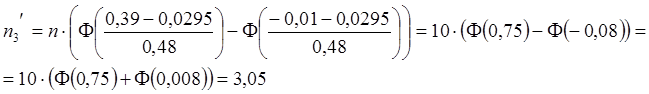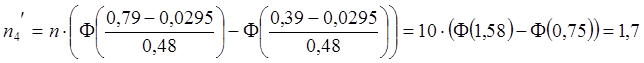
Сравним эмпирические и теоретические частоты, используя критерий Пирсона

[-0,81;-0,41]	1	1,39	-0,39	0,1521	0,109
[-0,41;-0,01]	3	2,89	0,11	0,0121	0,004
[-0,01;0,39]	1	3,05	-2,05	4,2025	1,378
[0,39;0,79]	4	1,7	2,3	5,29	3,112
сумма	10

Найдем по таблице критических точек распределения по уровню значимости  и числу степеней свободы критическую точку правосторонней критической области .

Так как наблюдаемое значение критерия больше  критического значения критерия , то делаем вывод о том, что наблюдения не согласуются с нормальным  распределением с параметрами 0, 0295 и 0,48  на уровне значимости .

Из представленных распределений указанная выборка лучше всего согласуется с равномерным распределением на отрезке , т.к. в этом случае получено наименьшее наблюдаемое значение критерия.

Часть II: Математическая статистика (практикум)

Задание 1.

По данной выборке X_i выполните следующие вычисления:

а) постройте гистограмму, полигон, выборочную функцию распределения;

б) вычислите выборочные моменты и связанные величины (первый, второй, третий, дисперсию, СКО, эксцесс и коэффициент асимметрии);

в) оцените методом моментов или/и методом максимального правдоподобия по выборке параметры основных непрерывных распределений (равномерное, экспоненциальное, нормальное и пр.), оцените близость оценок теоретических распределений к выборочному; подберите качественное описание выборочного распределения теоретическим;

г) предположив, что выборка получена из нормального распределения, протестируйте гипотезы равенства среднего нулю при неизвестной дисперсии; равенства среднего нулю при дисперсии, равной выборочной;

Числовые данные