Формула полной вероятности и вычисление вероятности события. Ковариация двух случайных величин, страница 2

Решение. В данной задаче идет речь о независимых испытаниях () в каждом из которых событие А – выпал «орел» может появиться с вероятностью 0,69, а событие  В – выпала «решка» с вероятностью 0, 31.

Случайные величины : x — количество выпавших «орлов», y — количество выпавших «решек» распределены по биномиальному закону:

вероятность того, что случайная величина  примет значение, равное может быть вычислена по формуле

, вероятность того, что случайная величина  примет значение, равное может быть вычислена по формуле

.

Для того, чтобы найти математические ожидания, вторые моменты и дисперсии данных случайных величин, составим их производящие функции. Так как формула Бернулли получается из разложения бинома Ньютона, то очевидно, что

 - производящая функция случайной величины ,

 - производящая функция случайной величины .

Тогда для случайной величины  имеем:

,

,

.

Тогда для случайной величины  имеем:

,

,

.

.

Случайная величина   - постоянная величина, принимающая значение, равное 252 с вероятностью 1.

Поэтому , .

Случайная величина , поэтому ,

.

б) опишите условное распределение с.в. x|y;

Решение. Вероятность  может принимать только два значения.

, если  и , если . в) в процессе подбрасывания на 142-том броске оказалось, что уже выпало ровно 80 «орлов», какова вероятность того, что всего выпадет не более 55 решек?

Решение. Найдем вероятность того, что событие А – выпал «орел» в 142 испытаниях произошло ровно 80 раз. Для этого воспользуемся локальной формулой Лапласа:

, .

В нашем случае , , , .

Поэтому ,

.

.

Найдем вероятность того, что в 252 подбрасываниях выпадет не более 55 «решек», т.е. не менее 197 «орлов», используя интегральную формулу Лапласа

, , .

В нашем случае , , , .

Поэтому

, .

.

Найдем вероятность того, что всего выпадет не менее 197 «орлов» при условии, что на 142-том броске уже выпало ровно 80 «орлов».

.

г) найдите ковариацию и коэффициент корреляции величин x и y;

Решение. Ковариация двух случайных величин может быть найдена по формуле

.

Так как , то .

.

Поэтому

.

Следовательно,

.

Вычислим коэффициент корреляции

д) найдите ковариацию и коэффициент корреляции величин x² и y;

Решение. Ковариация двух случайных величин  x² и y может быть найдена по формуле

.

Так как , то .

.

,

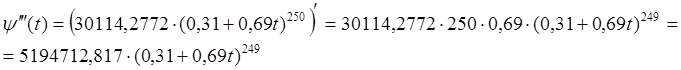
Поэтому

.

Следовательно,

.

Найдем дисперсию случайной величины  по формуле

.

.

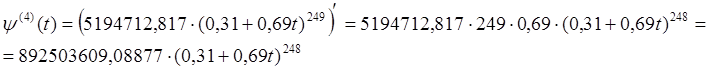
Вычислим коэффициент корреляции

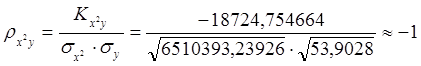
Задача 3.

Срок службы электрической лампы имеет показательное распределение с математическим ожиданием L часов. Ответьте на следующие вопросы:

а) какова вероятность того, что лампа прослужит от m₁ до M₁ часов?

б) какова вероятность того, что прослужившая уже m₂ часов лампа прослужит еще не менее M₂ часов?

в) какова вероятность того, что средний срок службы для N₃ ламп составит не менее M₃ часов?

г) какова вероятность того, что для N₄ ламп срок службы составит от m₄ до M₄ часов?

Числовые данные

L=76; m1=75; M1=109; m2=77; M2=99; N3=820; M3=81; N4=890; m4=93; M4=139.

Решение

Плотность распределения величины X(срок службы электрической лампы) имеет вид:

, где .

Функция распределения имеет вид: .

a) ;

б) .

в) сроки службы ламп друг от друга независимы. Введём в рассмотрение событие  — средний срок службы i-ой лампы составил не менее M3  часов. Интересующее нас событие , то есть одновременное наступление событий , то есть их произведение. Тогда по теореме о произведении вероятностей

г) так как события  независимы,

Задача 4.

Рассмотрите случайную выборку Xi из некоторого известного распределения и ответьте на следующие вопросы:

а) найдите оценку параметра A методом моментов, если известно, что выборка сделана из равномерного распределения U(–1;A)

б) найдите оценку методом моментов параметра B, если известно, что выборка сделана из равномерного распределения U(-B;B)

в) найдите оценки методом максимального правдоподобия параметров c и C, если известно, что выборка сделана из равномерного распределения U(c; C);