Формула полной вероятности и вычисление вероятности события. Ковариация двух случайных величин, страница 3

г) найдите (и сравните) оценки параметра L методом моментов и методом максимального правдоподобия, если известно, что выборка сделана из экспоненциального E_L распределения;

д) найдите оценку параметра m методом моментов, если известно, что выборка сделана из нормального распределения N(m, 1)

е) найдите оценки параметров M и S любым известным методом, если известно, что выборка сделана из нормального распределения N(M, S);

ж) постройте гистограмму и полигон по выборке, количество интервалов — K;

з) в каждом из пунктов (а) — (е) оцените близость данного теоретического распределения к эмпирическому на основе критерия Пирсона; какое из распределений (а) — (е) лучше описывает выборку?

Числовые данные

i1=-0,036;

i2=-0,809;

i3=0,315;

i4=-0,265;

i5=0,471;

i6=-0,386;

i7=0,576;

i8=-0,556;

i9=0,508;

i10=0,477;

K=3

Решение

а) найдите оценку параметра A методом моментов, если известно, что выборка сделана из равномерного распределения U(–1;A)

Решение. Известно, что для равномерно распределенной на отрезке случайной величины математическое ожидание может быть вычислено по формуле . Точеной оценкой математического ожидания является среднее арифметическое .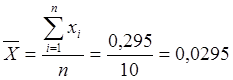

В нашем случае имеем .

б) найдите оценку методом моментов параметра B, если известно, что выборка сделана из равномерного распределения U(-B;B).

Решение. Известно, что для равномерно распределенной на отрезке случайной величины дисперсия может быть вычислено по формуле . Точеной оценкой дисперсии является выборочная дисперсия  .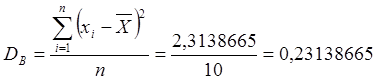

В нашем случае имеем

в) найдите оценки методом максимального правдоподобия параметров c и C, если известно, что выборка сделана из равномерного распределения U(c; C);

Решение.

Запишем функцию плотности вероятностей

.

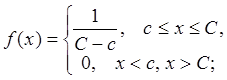
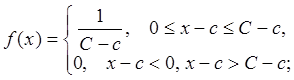Пусть , тогда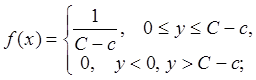

Составим функцию правдоподобия:

если , , …, , т.е , то

.

Если , то , поскольку в этом случае хотя бы один из сомножителей указанного произведения обращается в нуль.

График функции правдоподобия при оценке параметра равномерного распределения имеет вид

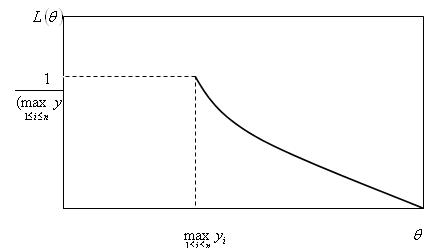
Наибольшее значение функции правдоподобия находиться в точке , т.е. .

г) найдите (и сравните) оценки параметра L методом моментов и методом максимального правдоподобия, если известно, что выборка сделана из экспоненциального E_L распределения;

Решение. Пусть наблюдаемая в эксперименте случайная величина  имеет экспоненциальное распределение с плотностью

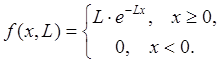
Применяя метод максимального правдоподобия, найдем точечную оценку для параметра .

Составим функцию правдоподобия 

.

Применяя операцию логарифмирования, получаем

.

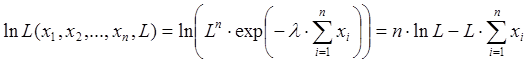Следовательно, уравнение правдоподобия имеет вид

.

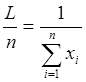
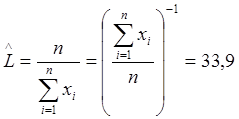Применяя метод моментов, найдем точечную оценку для параметра .

Найдем математическое ожидание случайной величины, имеющей экспоненциальное распределение:

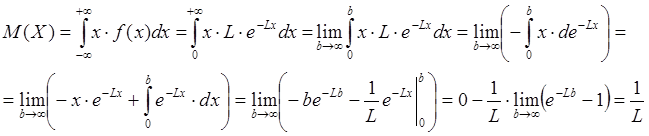
Так как точеной оценкой математического ожидания является среднее арифметическое 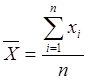, то получаем .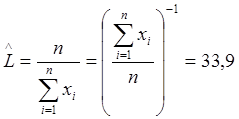

Применяя два различных метода, мы получили один и тот же результат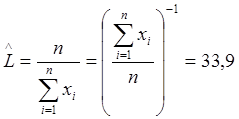

д) найдите оценку параметра m методом моментов, если известно, что выборка сделана из нормального распределения N(m, 1).

Решение. Пусть непрерывная случайная величина распределена по нормальному закону с параметрами  и .

Тогда плотность вероятности имеет вид

.

Найдем математическое ожидание случайной величины :

.

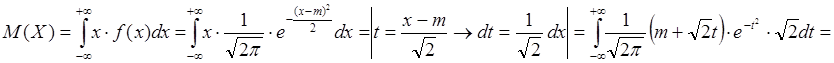
Первый интеграл равен нулю как интеграл от нечетной функции по симметричному относительно начала координат промежутку, второй интеграл  - интеграл Эйлера-Пуассона.

Так как точеной оценкой математического ожидания является среднее арифметическое 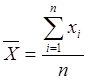, то получаем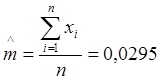

е) найдите оценки параметров M и S любым известным методом, если известно, что выборка сделана из нормального распределения N(M, S);

Решение. Пусть непрерывная случайная величина распределена по нормальному закону с параметрами  и .

Тогда плотность вероятности имеет вид

.

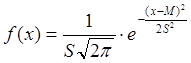Найдем математическое ожидание случайной величины :

.

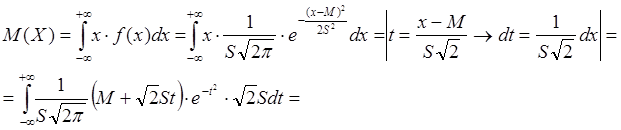
Первый интеграл равен нулю как интеграл от нечетной функции по симметричному относительно начала координат промежутку, второй интеграл  - интеграл Эйлера-Пуассона.