Формула полной вероятности и вычисление вероятности события. Ковариация двух случайных величин, страница 10

Протестируем принадлежность остатка модели регрессии  Y=kX+d, k=5.09, d=0.02 к нормальному распределению. Будем использовать критерий Пирсона. Для этого разобьём область (-0.08, 0.022) на 5 интервалов с границами -0.08, -0.025, -0.021, -0.017, -0.013, 0.022 и подсчитаем число элементов выборки, попавших в каждый интервал. Вычислим гипотетическую вероятность попадания в эти же интервалы случайной величины Z~N(0,0.02) (распределение остатков модели должно иметь математическое ожидание 0; дисперсия вычислена по выборке).

По таблице можно заключить, даже не вычисляя реализацию статистики , что эмпирическая (выборочная) частоты слишком отличаются, чтобы принадлежать одному распределению. Всё же вычислим её: . Это значение соответствует очень малому уровню значимости(меньше 0.01), поэтому гипотезу следует отвергнуть.

Протестируем принадлежность остатка модели регрессии  X=aY+b. а=0.2, b=-0.03 к нормальному распределению. Будем использовать критерий Пирсона. Для этого разобьём область (-0.8, 0.8) на 5 интервалов с границами -0.8, -0.2, 0.025, 0.05, 0.1, 0.8 и подсчитаем число элементов выборки, попавших в каждый интервал. Вычислим гипотетическую вероятность попадания в эти же интервалы случайной величины Z~N(0,0.305) (распределение остатков модели должно иметь математическое ожидание 0; дисперсия вычислена по выборке).

, поэтому гипотезу о принадлежности остатков модели к нормальному распределению следует отвергнуть.

Построим доверительный интервал для математического ожидания величины Y следующим образом:

,

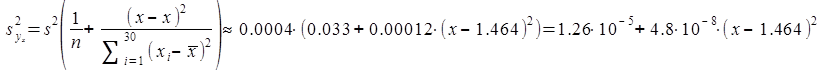
где  – стандартная ошибка групповой средней , ,   – выборочная остаточная дисперсия (дисперсия остатка модели); статистика  при  примет значение 2.05. Таким образом,

или .

Построим график зависимости ожидаемых значений Y при известных значениях Х.

Как и следовало ожидать (судя по величине остатков моделей), графики на рисунке выше неразличимы.