Формула полной вероятности и вычисление вероятности события. Ковариация двух случайных величин, страница 6

вариант:	6
i	Xi
1	0,15
2	-3,28
3	5,13
4	0,19
5	-40,44
6	11,06
7	-2,17
8	0
9	0,26
10	-7,68
11	0,33
12	-8,03
13	0,37
14	23,67
15	44,56
16	-1,62
17	42,31
18	2,62
19	21,84
20	-1,7
21	-0,49
22	-0,2
23	0,35
24	-32,11
25	13,72
26	-0,02
27	-1,95
28	-12,02
29	-7,96
30	-2,97

Решение:

а) Построим гистограмму, полигон, выборочную функцию распределения.

По данной выборке построим интервальный вариационный ряд, выделив пять частичных интервалов: -40 – -23, -23 – -6, -6 – 11, 11 – 28, 28 – 45. Длина частичных интервалов . Полученный интервальный статистический ряд запишем в виде таблицы:

Найдем плотность частоты и запишем в таблицу:

Построим полигон и гистограмму:

 

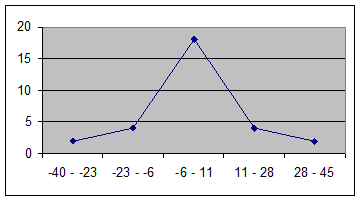
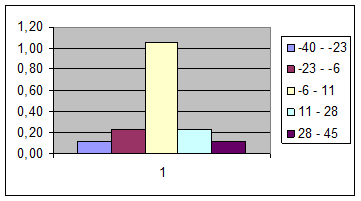
Из интервального ряда составим вариационный ряд, выбрав в качестве вариант середины интервалов. Запишем полученный ряд в виде таблицы:

Построим выборочную функцию распределения , учитывая, что объем выборки .

Значения  наблюдались 0 раз; следовательно,  при .

Значения  наблюдались 2 раза; следовательно,  при . Значения  наблюдались 6 раз; следовательно,  при .

Значения  наблюдались 24 раза; следовательно,  при . Значения  наблюдались 28 раз; следовательно,  при .

Значения  наблюдались 30 раз; следовательно,  при .

Выборочная функция распределения  имеет вид:

.

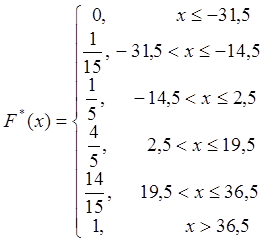б) Вычислим выборочные моменты и связанные величины (первый, второй, третий, дисперсию, СКО, эксцесс и коэффициент асимметрии). Воспользуемся методом произведений, для чего составим расчетную таблицу: варианты записываем в первый столбец; частоты – во второй, сумму частот поместим в нижнюю клетку столбца

1	2	3	4	5	6	7
-31,5	2	-2	-4	8	-16	32
-14,5	4	-1	-4	4	-4	4
2,5	18	0	0	0	0	0
19,5	4	1	4	4	4	4
36,5	2	2	4	8	16	32