Формула полной вероятности и вычисление вероятности события. Ковариация двух случайных величин, страница 4

Так как точеной оценкой математического ожидания является среднее арифметическое 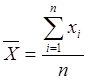, то получаем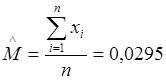

Найдем дисперсию случайной величины :

.

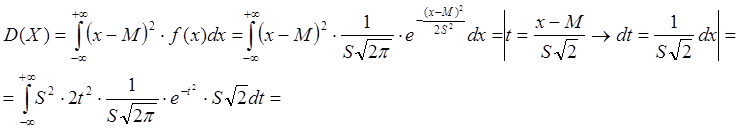
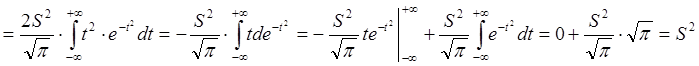Точеной оценкой дисперсии является выборочная дисперсия  .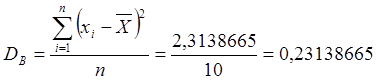

Поэтому

ж) постройте гистограмму и полигон по выборке, количество интервалов — 3;

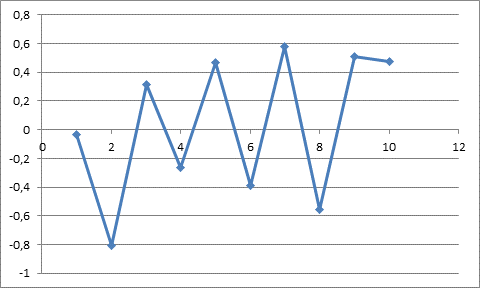
Найдем максимальное и минимальное значения по выборке:

 , .

Размах варьирования .

Рассмотрим три равных частичных интервала, в которые попадают все элементы выборки

	[-0,81;-0,34]	[-0,34;0,13]	[0,13;0,6]
	3	2	5

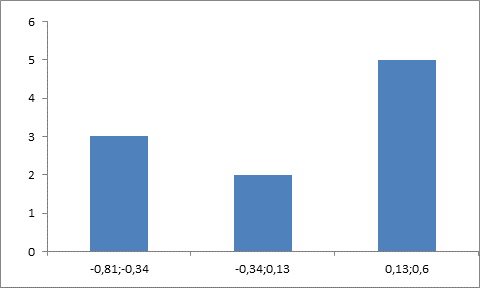
з) в каждом из пунктов (а) — (е) оцените близость данного теоретического распределения к эмпирическому на основе критерия Пирсона; какое из распределений (а) — (е) лучше описывает выборку?

Решение.

	[-0,81;-0,41]	[-0,41;-0,01]	[-0,01;0,39]	[0,39;0,79]
	2	3	1	4

В пункте а) была найдена оценка параметра .

Найдем плотность предполагаемого равномерного распределения на отрезке

,

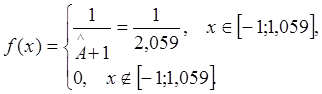Найдем теоретические частоты:

,

,

,

Сравним эмпирические и теоретические частоты, используя критерий Пирсона

[-0,81;-0,41]	2	1,94	0,06	0,0036	0,0019
[-0,41;-0,01]	3	1,94	1,06	1,1236	0,5792
[-0,01;0,39]	1	1,94	-0,94	0,8836	0,4555
[0,39;0,79]	4	1,94	2,06	4,2436	2,1874
сумма	10

Найдем по таблице критических точек распределения по уровню значимости  и числу степеней свободы критическую точку правосторонней критической области .

Так как наблюдаемое значение критерия меньше критического значения критерия (3,224<3,8), то делаем вывод о том, что наблюдения согласуются с равномерным распределением на рассматриваемом отрезке на уровне значимости .

В пункте б) была найдена оценка параметра .

Найдем плотность предполагаемого равномерного распределения на отрезке

,

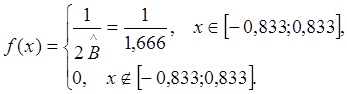Найдем теоретические частоты:

,

,

,

Сравним эмпирические и теоретические частоты, используя критерий Пирсона

[-0,81;-0,41]	2	2,4	-0,4	0,16	0,0667
[-0,41;-0,01]	3	2,4	0,6	0,36	0,15
[-0,01;0,39]	1	2,4	-1,4	1,96	0,8167
[0,39;0,79]	4	2,4	1,6	2,56	1,0667
сумма	10

Найдем по таблице критических точек распределения по уровню значимости  и числу степеней свободы критическую точку правосторонней критической области .

Так как наблюдаемое значение критерия меньше критического значения критерия (2,1001<3,8), то делаем вывод о том, что наблюдения согласуются с равномерным распределением на рассматриваемом отрезке на уровне значимости .

В пункте u) была найдена оценка параметра .

Найдем плотность предполагаемого экспоненциального распределения ,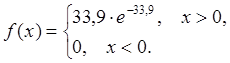

Найдем теоретические частоты:

,

,

,

Сравним эмпирические и теоретические частоты, используя критерий Пирсона

[-0,81;-0,41]	2	8419603071104	-8419603071102	8419603071100
[-0,41;-0,01]	3	10870723	-10870720	10870715
[-0,01;0,39]	1	474,6	-473,6	472,6
[0,39;0,79]	4	0,0007	3б9993	22849,14
сумма	10