Аффинные преобразования плоскости и пространства. Изометрические преобразования (ИП). Связь с движениями.

Раздел I

Аффинные преобразования плоскости и пространства

 Определение. Биективное отображение множества точек плоскости (пространства) на себя называется преобразованием плоскости (пространства).

Определение. Пусть на плоскости введены 2 АСК: I: Oē₁ē₂ и I’: O’ē’₁ē’₂, тогда преобразование плоскости при котором АСК I переходит в АСК I’, а произвольная т. М переходит в некоторую т. М’, которая в АСК I’ имеет те же координаты, что и т.М в АСК I, называется аффинным преобразованием  (АП) плоскости.

М(х;у) в I

M→ М’(х;у) в I’

Определение.Пусть в пространстве введены 2 АСК: I:Oē₁ē₂ē₃ и I’: O’ē’₁ē’₂ē’₃, тогда преобразование пространства, при котором АСК I переходит в I’, а произвольная т.М переходит в т.М’, которая в АСК I’ имеет те же координаты что и т.М в АСК I, называется аффинным преобразованием пространства.

М(х;у;z) в I

M→ М’(х;у;z) в I’

Частный случай

Определение. АПплоскости (пространства), в которой ПДСК переходит в ПДСК, называется движением плоскости (пространства).

А – аффинное преобразование.

Д – движение.

М(x;y) в ПДСК Oīj (I)

Д

М → М’

М’(x;y) в ПДСК O’ī’j’ (I’)

М₁(x₁;y₁) в I М₁’(x₁;y₁) в I’

М₂(x₂;y₂) в I М₂’(x₂;y₂) в I’

          Только ПДСК!!!

Утверждение

При движении расстояние между точками сохраняется.

Доказательство выше.

Свойства аффинных преобразований

 Если при АП А  , если  в I , то и  в I’

Доказательство:

Пусть

М₁(x₁;y₁) М₂(x₂;y₂) в I

А

М₁→ М₁’(x₁;y₁) в I’

М₂→М₂’(x₂;y₂) в I’

 в I’

                        ч.т.д.

 При А     

Доказательство:

 в I

 в I

  в I

в силу свойства

 в I’

 в I’

 в I’

 в I’

 

 

 

Доказательство:

 в I

 в I

 в I’

 в I’

 в I’ =>  

 

 Пусть имеем  и набор чисел

, тогда

 

 

Доказательство:

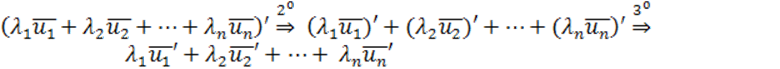
 Линейно-зависимая система векторов при А переходит в линейно зависимую систему.

Пусть  – лин. завис. система векторов

, где хотя бы одно число ≠0, для этой системы векторов выполняется равенство

 

А

 

 

=>- л/з по определению.

 Преобразование обратное к аффинному преобразованию тоже является аффинным преобразованием.

I                            I’

    

М(x;y) в I→М’(x;y) в I’

 

М(x;y) в IМ’(x;y) в I’

Преобразование А^-1 удовлетворяет определению аффинного преобразования.

 Линейно-независимая система векторов при аффинном преобразовании переходит в линейно-независимую систему.

Доказательство: от противного.

Пусть лин.независ. сист. лин.завис. сист.

лин.независ. сист. лин.завис. сист.

Это противоречит свойству , получили противоречие. Наше предположение неверно.

л/н. сист. л/н. сист.

 Пусть имеется аффинное преобразование A

    

I                            I’

М(x;y) в I→М’(x;y) в I’

тогда, если при этом преобразовании  АСК (репер)

    

II                           II’

то для произв. т.М выполняется условие:

M(ξ;η) в II→ M’(ξ;η) в II’

(это свойство позволяет менять системы координат в определении А).

 Композиция двух аффинных преобразований в плоскости А₁ и А₂ является снова аффинным преобразованием плоскости.

А₁                                                       А₂

I→I’                                                   II→II’

М(x;y) в I→М’(x;y) в I’                    Р(ξ;η) в II→ Р’(ξ;η) в II’

Рассмотрим, в какую АСК перейдет система  I’ при преобразовании А₂. Пусть 

В силу свойства  точка М’

 

 – композиция A₁ и A₂

АСК      

 

Таким образом, композиция двух аффинных преобразований является аффинным преобразованием по определению.

 Пусть E – тождественное преобразование плоскости, оно является аффинным. (def)

E – единица в группе аффинных преобразований.

 Рассмотрим аффинное преобразование А и А^-1 оно является аффинным по .

Рассмотрим композицию:

М →М’→М

 

 Ассоциативность

 

 Множество всех преобразований плоскости (пространства) образуют группу, где групповой операцией является композиция аффинных преобразований (доказательство на основании свойств ).

Свойства прямых и плоскостей и других геометрических фигур  при аффинном преобразовании.

 При АП множество точек плоскости, удовлетворяющее уравнению

(1)   F(x;y) = 0 в АСК I, переходит во множество точек плоскости, которое удовлетворяет этому же уравнению, но в АСК I’.

Следствие

 При АП плоскости прямая → прямую, эллипс → эллипс, гипербола → гиперболу, парабола→параболу. (в силу 14^о).

Свойство, аналогичное  справедливо для пространства.

14^о’. Множество точек пространства, удовлетворяющее уравнению

(2)  F(x;y;z)=0 в I, при аффинном преобразовании A

переходит во множество точек пространства, которое удовлетворяет уравнению (2), но в системе I’.

 При АП плоскости и пространства: параллельные прямые→в параллельные прямые, а параллельные плоскости→в параллельные плоскости.

Доказательство:

в I          в I’

в I          в I’

после АП плоскости переходят в такие же плоскости, которые в системе I’ имеют такие же уравнения, что и в системе I

 

 

Аналитическое задание АП

   

М(x;y) в I→М’(x;y) в I’

Пусть М’(x’;y’) в I .

Рассмотрим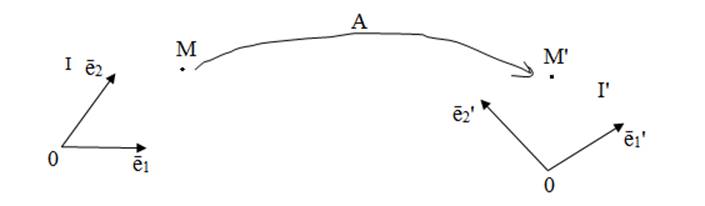

Как связаны координаты точек М’(x’;y’) и М(x; y) в старой системе I?

Для ответа на этот вопрос рассмотрим координаты точки М’ в старой и в новой системах координат: М’(x;y) в I’ , но М’(x’;y’) в I.

Запишем формулы преобразования аффинной системы координат для координат точки М’ (1 семестр)

 , где                                                                  (3)

ē’₁           ē’₂       O’

 

 

O’(a;b) в I

Возвращаясь к логике АП плоскости, видим, что формула (3) дает нам связь координат т. М’(x’;y’) в I и М(x;y) в I.

Аналогично выводятся формулы АП в пространстве.

Oē₁ē₂ē₃ O’ē’₁ē’₂ē’₃

II’

 

 

 

O’(a;b;c) в I

М(х;у;z) в I  М’(х;у;z) в I’

М’(х’;у’;z’) в I

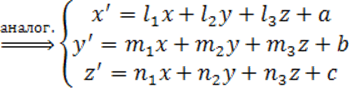  (4)

(3)  и (4) – формулы АП плоскости и пространства.

Сохранение отношений площадей фигур

при аффинном преобразовании плоскости