Т: ![]() – перенос плоскости на вектор {a;b}
– перенос плоскости на вектор {a;b}
Утверждение.Преобразование DC можно представить в виде композиции DC0 и Т, т.е. поворота плоскости вокруг начала координат на угол φ и переноса на вектор {a;b}.
С другой стороны преобразование DC при ненулевом угле φ равносильно повороту плоскости вокруг т.М0 (без переноса).
Рассмотрим несобственное движение.
DН : (VVV) ![]()
Рассмотрим частный случай.
φ=0 a=b=0
Sx: ![]() симметрия относительно оси Ох
симметрия относительно оси Ох
Утверждение
Любое DН представимо в виде композиции
![]()
Изометрические преобразования (ИП). Связь с движениями.
Определение. АП, при котором сохраняется скалярное произведение векторов, называется изометрическим преобразованием.
![]()
![]()
![]()
Свойства изометрических преобразований
![]() При ИП длины векторов сохраняются.
При ИП длины векторов сохраняются.
![]()
![]()
![]() ,
, ![]() .
.
Следствие. При ИП сохраняется расстояние между точками.
![]() совпадают со свойствами движения 1, 2, 3, 4, их
доказательства так же совпадают.
совпадают со свойствами движения 1, 2, 3, 4, их
доказательства так же совпадают.
Теорема о связи ИП и Д.
Любое ИП – это движение, любое движение – это ИП.
Доказательство:
1) имеем ИП.
Докажем, что это движение.
![]() – ПДСК
– ПДСК ![]()
![]()
![]()
![]()
![]() в силу
в силу ![]() ИП
ИП
![]() - ПДСК
- ПДСК
При ИП ПДСК→в ПДСК =>оно движение по определению.
2) пусть имеем D – произвольное движение.
Докажем что это ИП
![]()
![]()
т.к. при движении расстояние между точками сохраняется.
![]()
![]() в силу
в силу ![]() движения
движения
![]()
![]()
=>Движение есть ИП по определению.
Гомотетия. Преобразование подобия.
Определение.
Гомотетией Г с центром в т. М0 и коэффициентом kназывают АП
плоскости, при котором т. М ![]() М’, так что
М’, так что ![]() , где М0 – двойная точка.
, где М0 – двойная точка.
Формулы гомотетии.
![]() Пусть M0(x0;y0), M(x;y), M’(x’;y’)
Пусть M0(x0;y0), M(x;y), M’(x’;y’)
![]()
![]()
![]()
![]()
![]()
![]()
![]() =>Г:
=>Г: ![]()
Г. с центром в начале координат O и k
Г0: ![]()
 |
Свойства гомотетии
![]() При гомотетии с коэффициентами k
расстояние между точками изменяется в k раз.
При гомотетии с коэффициентами k
расстояние между точками изменяется в k раз.
Доказательство:
|
|
|
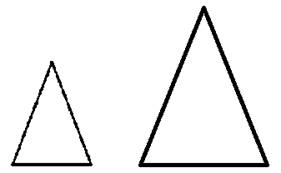
![]() При гомотетии треугольники переходят в треугольники,
подобные первоначальным.
При гомотетии треугольники переходят в треугольники,
подобные первоначальным.
Доказательство: Признак подобия по трем сторонам.
![]() При гомотетии углы между векторами сохраняются.
При гомотетии углы между векторами сохраняются.
Доказательство: из ![]() свойства.
свойства.
Δ→ в подобные Δ, а углы между соответствующими сторонами в подобных треугольниках равны.
![]() При гомотетии с коэффициентом k
площади Δ изменяются в k2 раз.
При гомотетии с коэффициентом k
площади Δ изменяются в k2 раз.
Доказательство:
![]()
![]()
![]()
![]()
![]()
Преобразование подобия (ПП).
Определение. АП, при котором расстояние между любыми двумя точками изменяется в k раз, называется преобразованием подобия с коэффициентом k.
Свойства преобразования подобия
![]() При ПП Δки→ в Δки подобные
первоначальным, с коэффициентом подобия k.
При ПП Δки→ в Δки подобные
первоначальным, с коэффициентом подобия k.
Доказательство: по определению.
![]() При ПП углы между векторами сохраняются.
При ПП углы между векторами сохраняются.
![]() При ПП площади треугольников изменяются в k2 раз.
При ПП площади треугольников изменяются в k2 раз.
Свойства 2 и 3 доказываются абсолютно аналогично, как и для гомотетии
Замечание. При ПП и при Г площадь любой замкнутой фигуры изменяется в k2 раз.
Теорема. Любое ПП с коэффициентом k можно представить в виде композиции гомотетии с коэффициентом k и некоторого движения.
Доказательство:
Пусть имеем ПП Pс коэффициентом k, при этом преобразовании расстояние между точками изменяется в k раз.
Рассмотрим Г с
коэффициентом ![]() и с центром в произвольной точке М0.
и с центром в произвольной точке М0.
При этой Г, в силу ее
свойств, расстояние между двумя любыми точками изменяется в ![]() раз.
раз.
Если мы выполним композицию этих преобразований, то получим, что расстояние между точками не изменилось. Следовательно, композиция этих преобразований – это некоторое движение.
![]()
Рассмотрим Г-1 – гомотетия с центром в точке М0 и коэффициентом k.
Возьмем вышеупомянутую композицию и умножим слева на Г-1.
![]()
![]()
![]()
![]() (*) ч.т.д.
(*) ч.т.д.
в формуле (*) центр гомотетии можно брать где угодно.
Формулы ПП
Рассмотрим гомотетию с центром в начале координат.
Г-1: ![]()
D: ![]()
Р(ПП): ![]() (**) – формула любого ПП с коэффициентом k.
(**) – формула любого ПП с коэффициентом k.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.