Аффинные преобразования плоскости и пространства. Изометрические преобразования (ИП). Связь с движениями., страница 2

Рассмотрим площадь параллелограмма, построенного на векторах  и .

 

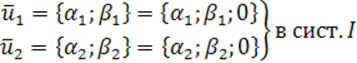
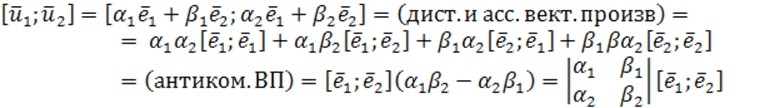
Пусть имеется преобразование А, которое переводит

I(Oē₁ē₂ )    I’(O’ē’₁ē’₂)

Каковы формулы преобразования для координат векторов?

 в I    в I’

 в I

 в I

 в I

в силу (3)

              

Аналогично

                                                                              (5)

формула АП для координат векторов

в I в I’

в I

в Iв I’

в I

в силу (5)

в I   (**)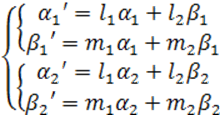

В силу (*)

 

В силу (**)

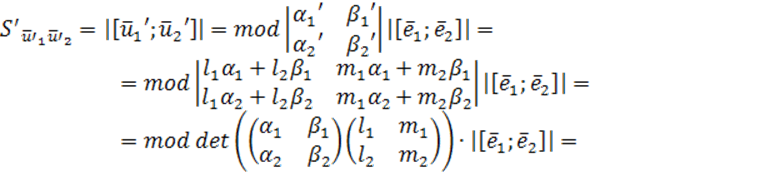
Из алгебры известен закон: определитель произведения двух квадратных матриц есть произведение определителей этих матриц.

det (A*B)=det A * det B

Пусть   – определитель матрицы АП

      (6)    площадь параллелограмма

Пусть S₁ и S₂ – площади двух параллелограммов

S₁  S₁’

S₂  S₂’

S₁’= S₁|J|

S₂’= S₂|J|

Теорема 1. При АП плоскости отношение площадей двух параллелограммов сохраняется.

Доказательство выше.

Рассмотрим произвольную фигуру на плоскости и разобьем ее на некоторое количество параллелограммов, так, чтобы они покрывали площадь фигуры, при стремлении числа параллелограммов к бесконечности. то можно сказать, что в пределе сумма площадей параллелограммов равна площади фигуры.

S_ф=S₁+S₂+…+S_n+…

S_ф'=|J|S₁+|J|S₂+…+|J|S_n+…=|J|( S₁+S₂+…+S_n+…)= |J|S_ф

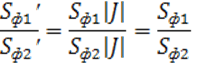
Теорема 1’. Отношение площадей плоских замкнутых фигур сохраняется при АП плоскости (доказательство выше).

Сохранение отношений объемов тел при аффинном преобразовании пространства.

Рассмотрим параллелепипед, построенный на трех векторах. Его объем равен:

 

 

                в Oē₁ē₂ē₃

 

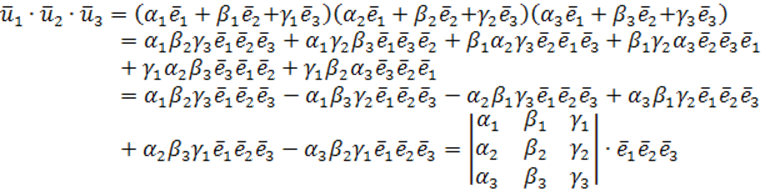
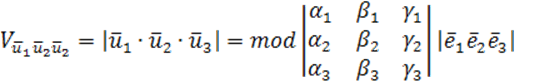(V)

Аффинное преобразование пространства. Выведем формулы преобразования координат вектора в пространстве. Преобразование координат точек:

 

 

 

 

 

 

 

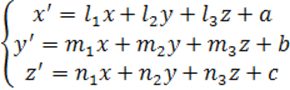
Рассмотрим преобразование трех векторов

 

       в I Oē₁ē₂ē₃  

 

  

  

  

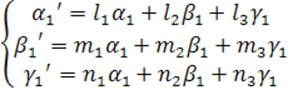
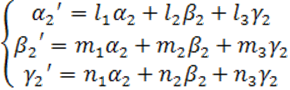
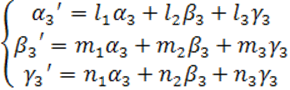
Рассмотрим V параллелепипеда, построенного на

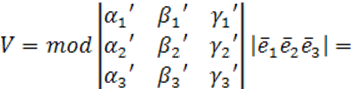
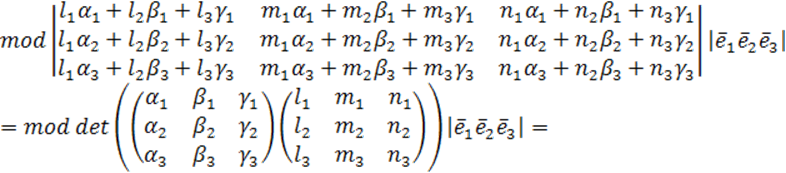
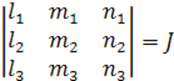 - определитель матрицы АП пространства

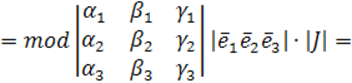(V)=

 

Для двух параллелепипедов

 

 

;

Мы доказали теорему.

Теорема 2. При АП пространства отношение объемов параллелепипедов сохраняется.

Утверждение. Отношение объемов тел при АП сохраняется.

Представление произвольного АП плоскости в виде композиции движения и двух сжатий по взаимно перпендикулярным направлениям.

Теорема 3. Любое АП плоскости можно представить в виде композиции движения и двух сжатий по взаимно перпендикулярным направлениям.

Лемма. При выполнении произвольного АП плоскости существуют два взаимно перпендикулярных направления плоскости, которые переходят в два взаимно перпендикулярные направления этой же плоскости.

Доказательство леммы:

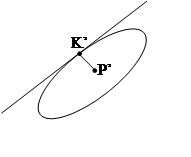Рассмотрим любое АП плоскости А и рассмотрим окружность с центром в т.Р.

	N’

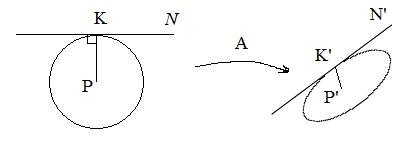
Мы знаем, что окружность эллипс.

Центр окружности т.Р  центр эллипса P’(центр симметрии)

Найдем на эллипсе (образе окружности) точку ближайшую к центру Р’, обозначим ее К’

К’Р’ – наименьшее расстояние до точек эллипса от его центра.

Пусть при АП А т.К (окр.) → т.К’ (элл.)

Рассмотрим касательную к окружности в т.К, по свойству касательной она перпендикулярна радиусу РК. Возьмем на касательной т.N, не принадлежащую PК.

При АП А касательная NK→в касательную эллипса N’K’.

Доказательство этого факта: (от противного)

Пусть K’N’ не является касательной. Тогда она пересечет эллипс в двух точках, но К не может перейти в две точки в силу определения отображения. Следовательно, K’N’ – касательная к эллипсу, где K’ – точка касания. Является ли отрезок K’P’ наименьшим расстоянием до прямой K’N’? Доказательство этого факта: (от противного) Пусть существует L’ | L’P’|<| K’P’| Тогда отрезок  L’P’ пересекает эллипс в некоторой точке H0. Но по условию , где Н0 – точка на эллипсе, но К’Р’ – наименьшее расстояние до точек эллипса от его центра, следовательно, по предположению | L’P’|<| Н0P’|<|K’P’|, противоречие.