Пояснительная записка к курсовой работе по прочности ”Расчет на прочность элементов конструкции самолета”, страница 14

.

Из этого условия определим отношение  и размер  

, .

Тогда .

В конце хода поршня  функция трения .

4.2.2.4 Определение приведенной длины газовой камеры

Приведенная длина газовой камеры  находится из соотношения

, где     -   показатель политропы, ;

.

Отношение  не должно превышать 0,8, иначе в конце хода поршня может возникнуть слишком большое давление  в камере амортизатора. Вычисленное значение превышает допустимое.

Уменьшим величину до значения .

Тогда

;

;

;

.

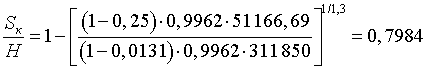Условие  выполняется.

Приведенная высота газовой камеры ,

4.2.2.5 Определение площади газового поршня, объема газовой камеры и уровня жидкости

Площадь газового поршня определяется по формуле

, где    . Примем .

Давление  примем равным 4 МПа. Тогда

.

По известной площади поршня, определяется начальный объем газовой камеры

, .

Высота уровня жидкости над верхней буксой находится по формуле

, где     -    максимальный ход поршня;

 - диаметр штока;

 -  внутренний диаметр цилиндра.

Примем .

Внутренний диаметр цилиндра определим из площади поршня:

, , .

Тогда высота уровня жидкости над верхней буксой

.

Из конструктивных соображений выберем площадь плунжера

.

Примем , . Диаметр плунжера

.

4.2.2.6 Определение площади проходных отверстий для гидросмеси

Площадь проходных отверстий определяется по формуле

, где     - скорость перемещения поршня;

 -   коэффициент гидравлического сопротивления, примем ;

 -   плотность гидросмеси, примем ;

 - сила сопротивления жидкости.

Силу сопротивления жидкости можно найти для любого значения хода поршня  по формуле

.

Для этого необходимо иметь диаграмму обжатия амортизатора .

Диаграмма проводится через две точки – при ,  и при , , так, чтобы площадь, ограниченная этой кривой, равнялась работе амортизатора , и кривая имела наибольшую ординату в конце хода поршня.

;

.

Диаграмма обжатия амортизатора представлена на Рис.18.

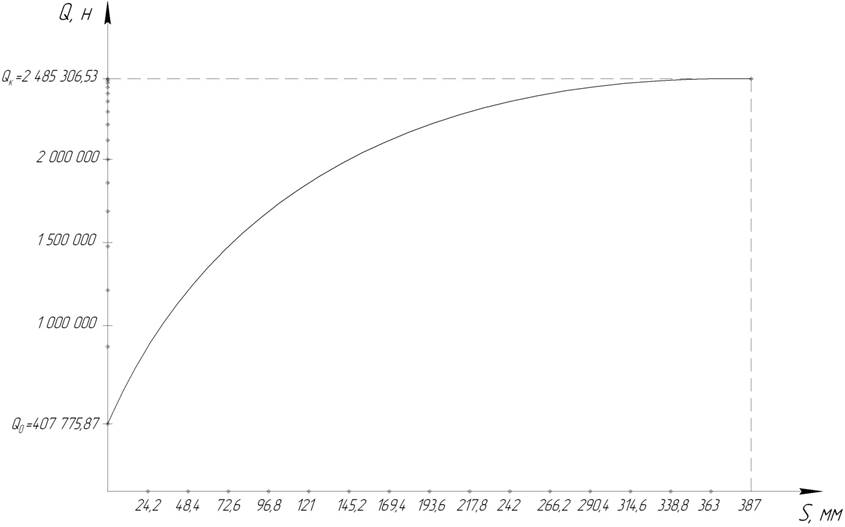
Рис. 18 Диаграмма обжатия амортизатора

Полный ход поршня разбивается на ряд небольших интервалов . На каждом интервале определяется скорость .

, где     -скорость опускания центра масс самолета;

, где     - приращение величины опускания центра масс самолета;

;

 -   приращение работы амортизатора;

 -   приращение работы пневматика;

, величины  снимаются с диаграммы .

Далее находится сила обжатия пневматика

и определяется приращение работы пневматика

.

Приращение величины опускания центра масс самолета

.

Скорость опускания центра масс самолета к моменту трогания поршня

, где     -   скорость опускания центра масс самолета к моменту касания пневматиками земли;

 -   обжатие пневматика к моменту трогания поршня, ;

 -    работа пневматиков к моменту трогания поршня;

, где     -  нормированная работа. Расчет будем вести по максимальной работе, ;

 -  обжатие пневматика к концу хода поршня, ;

;

Работа пневматиков к моменту трогания поршня определится

, ;

.

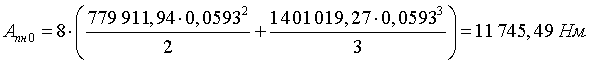Результаты расчета сведены в таблицу 14.

Диаграммы , ,  представлены на Рис.19.

Диаграммы , , ,  представлены на Рис. 20.

Рис. 19 Диаграммы , ,

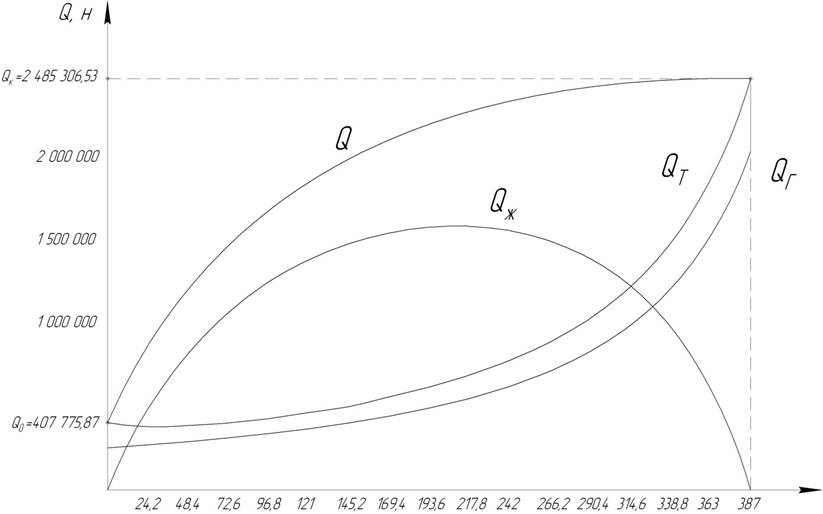
Рис. 20 Диаграмма обжатия амортизатора

4.3 Расчет шасси на прочность

4.3.1. Определение усилий в основных силовых элементах

Заданным расчетным случаем для шасси является случай Еш – посадка на три точки.

Эксплуатационная перегрузка

, .

Максимальный коэффициент эксплуатационной перегрузки

, .

Коэффициент безопасности

, . Примем .

Эксплуатационная нагрузка

, .

Расчетная нагрузка

, .

Нагрузка направлена перпендикулярно поверхности аэродрома. Т.к. стойка имеет угол выноса, то расчетная нагрузку можно разложить на две составляющие – направленную по оси стойки  и перпендикулярную оси стойки .

, ;

, ;

Необходимо учесть возможную несимметрию нагружения стойки. Поэтому распределим нагрузку следующим образом

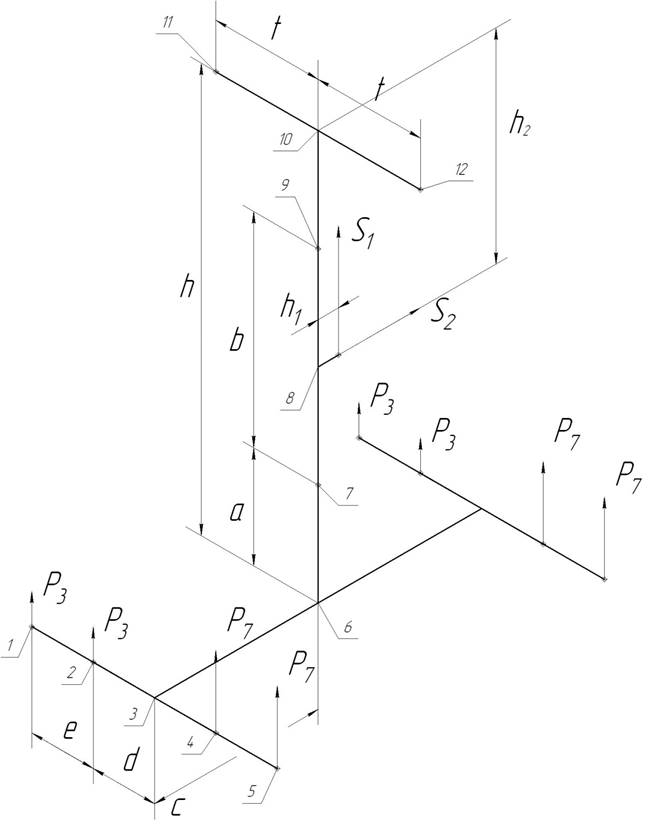
Рис. 21 Распределение нагрузки на стойке

На Рис.21 обозначено:

, ;

, .

Пусть подкос подходит к стойке под углом . Тогда . Силы в подкосе и

, .

Примем следующие геометрические параметры стойки:

, ;

, ;

, , , , , , .