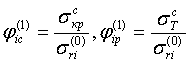 (2.19)
(2.19)
Повторяем расчет до тех пор, пока в двух следующих друг за
другом приближениях значения редукционных коэффициентов станут близки к
заданной степени точности. Если для стрингеров окажется, что ![]() , то
следует принять для них
, то
следует принять для них ![]() .
Имея
.
Имея ![]() ,
вычисленные с заданной степенью точности, можно найти истинные нормальные
напряжения
,
вычисленные с заданной степенью точности, можно найти истинные нормальные
напряжения
![]() (2.20)
(2.20)
Выполним все приближения с помощью электронной таблицы Excel.
![]()
Тогда
![]()
Так как угол α мал, то за главные
центральные оси сечения принимаем оси ![]() .
.
Полученные в таблице редукционные коэффициенты больше единицы. Принимая их равными единице, мы получим те же самые результаты. Поэтому больше выполнять приближения не имеет смысла
Таблица 8. (Продолжение)
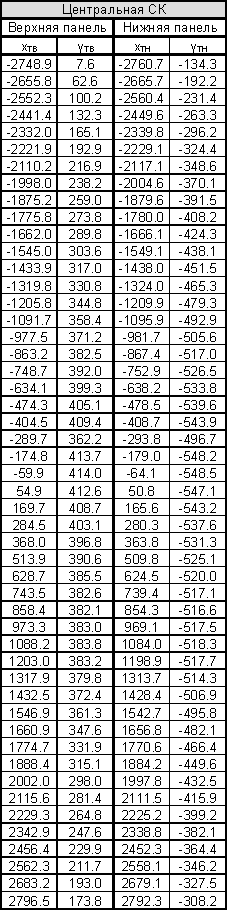
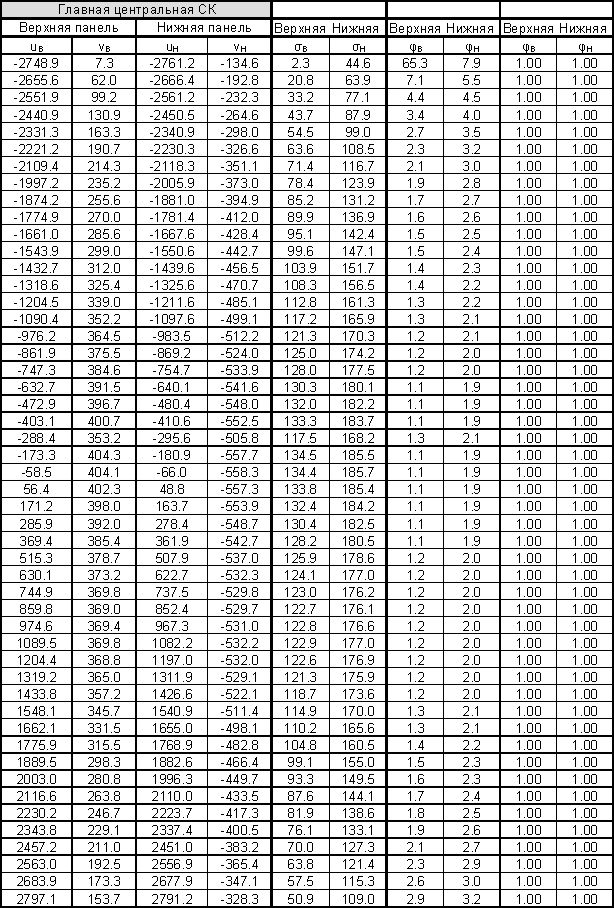
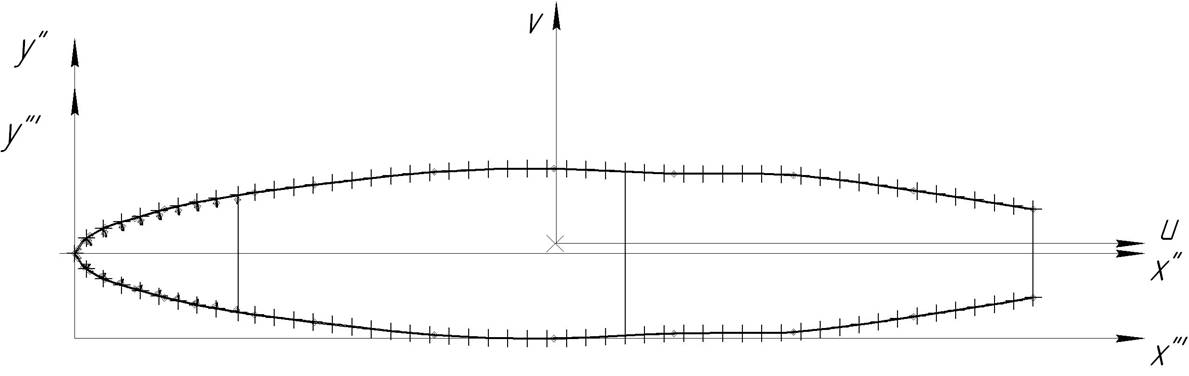
Рис.6 Сечение крыла
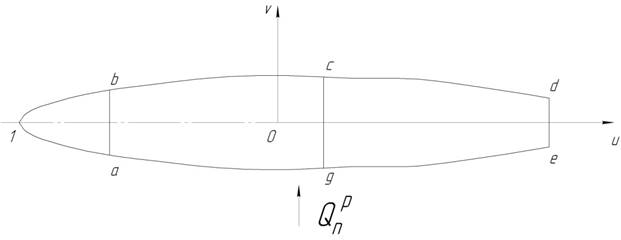
Рис. 7 К определению касательных напряжений при простом изгибе
Для любого участка i,i+1 сечения крыла касательное усилие при простом изгибе находится по формуле
![]() , где
, где ![]() - касательное
усилие на участке i, i+1 сечения в предположении, что в точках j = 1,2,... касательные
усилия равны нулю (каждая из этих точек служит началом отсчета дуг для
соответствующего контура);
- касательное
усилие на участке i, i+1 сечения в предположении, что в точках j = 1,2,... касательные
усилия равны нулю (каждая из этих точек служит началом отсчета дуг для
соответствующего контура);
![]() - вспомогательные
функции, Рис.8.
- вспомогательные
функции, Рис.8.
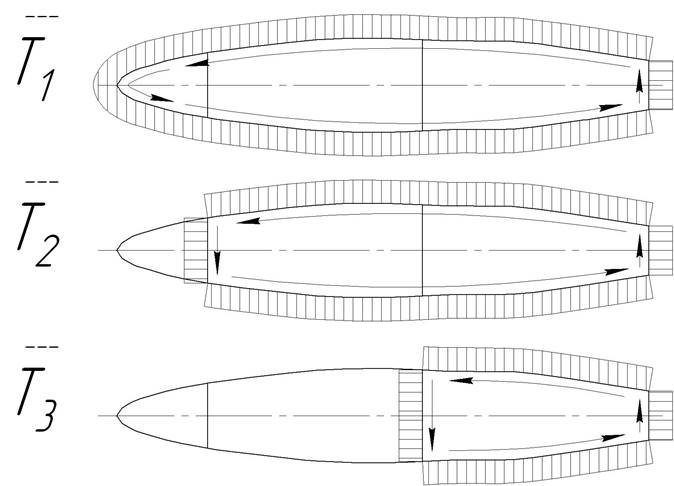
Рис.8 Вспомогательные единичные функции
Неизвестные усилия ![]() в точках
1,2,3 определяются из системы уравнений
в точках
1,2,3 определяются из системы уравнений
![]() ,
,
![]() , где
, где 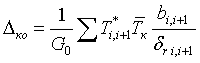 ;
;
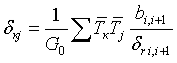 ;
;
![]() .
.
![]() - редукционный
коэффициент обшивки и стенок при работе на сдвиг
- редукционный
коэффициент обшивки и стенок при работе на сдвиг
![]() ;
;
Для обшивки принимаем ![]() , для
стенок лонжеронов
, для
стенок лонжеронов ![]() .
.
Усилия ![]() вычисляются
по формуле
вычисляются
по формуле
![]() .
.
Значения момента инерции приведенного сечения ![]() относительно
главной оси и, редуцированных площадей
относительно
главной оси и, редуцированных площадей ![]() элементов
продольного набора, расстояний
элементов
продольного набора, расстояний ![]() от
оси и до центров тяжести редуцированных площадей элементов берутся по
результатам последнего приближения расчета нормальных напряжений.
от
оси и до центров тяжести редуцированных площадей элементов берутся по
результатам последнего приближения расчета нормальных напряжений.
Доля перерезывающей силы, воспринимаемой обшивкой и стенками лонжеронов крыла, равна
![]() ,
,
![]() , где
, где ![]() - число
элементов продольного набора в сечении крыла;
- число
элементов продольного набора в сечении крыла;
![]() - угол
между осью i-го элемента продольного набора и
плоскостью хорд.
- угол
между осью i-го элемента продольного набора и
плоскостью хорд.
Результаты расчета касательных напряжений при простом изгибе сведены в таблицу 9.
Эпюры погонных касательных сил приведены на Рис.9.
Проверка правильности построения для эпюры ![]()
![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
, ![]() ;
;
для эпюры ![]()
![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
, ![]() ;
;
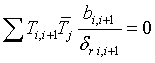 ,
,
 ,
, 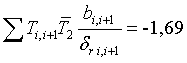 ,
, 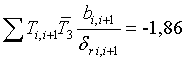 .
.
Таблица 9. Расчет касательных сил при простом изгибе
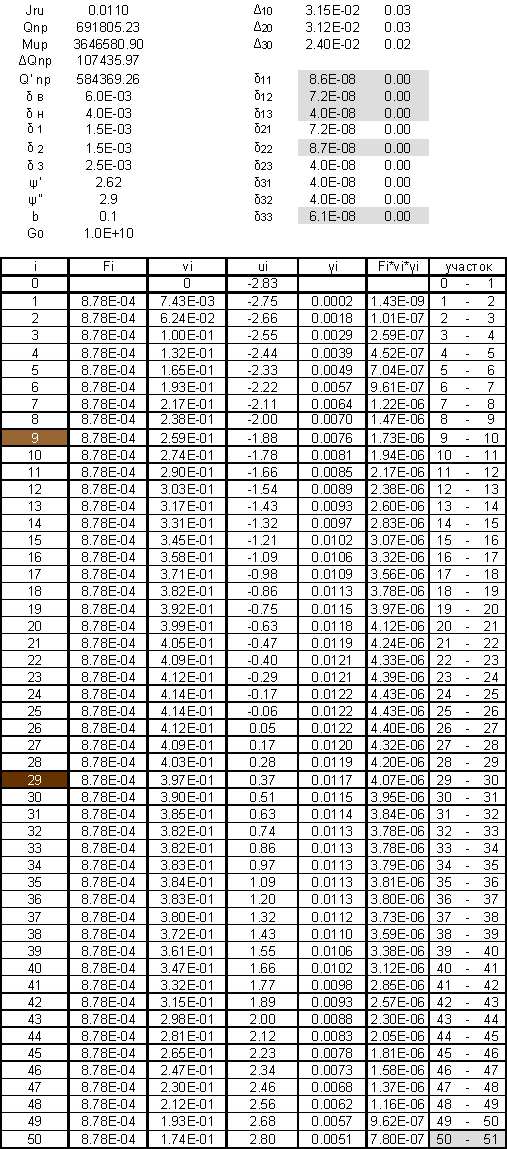
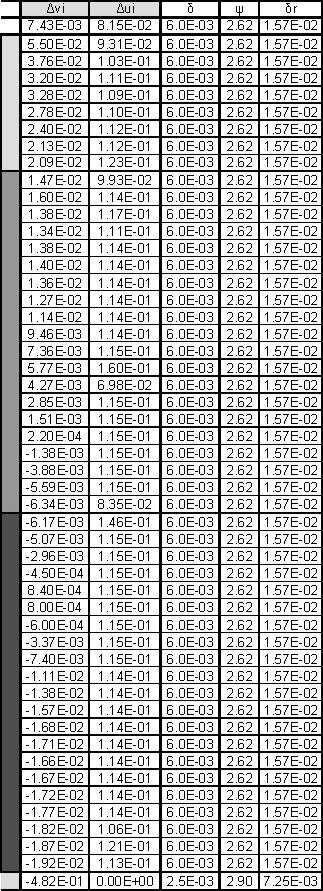
Таблица 9. (Продолжение)
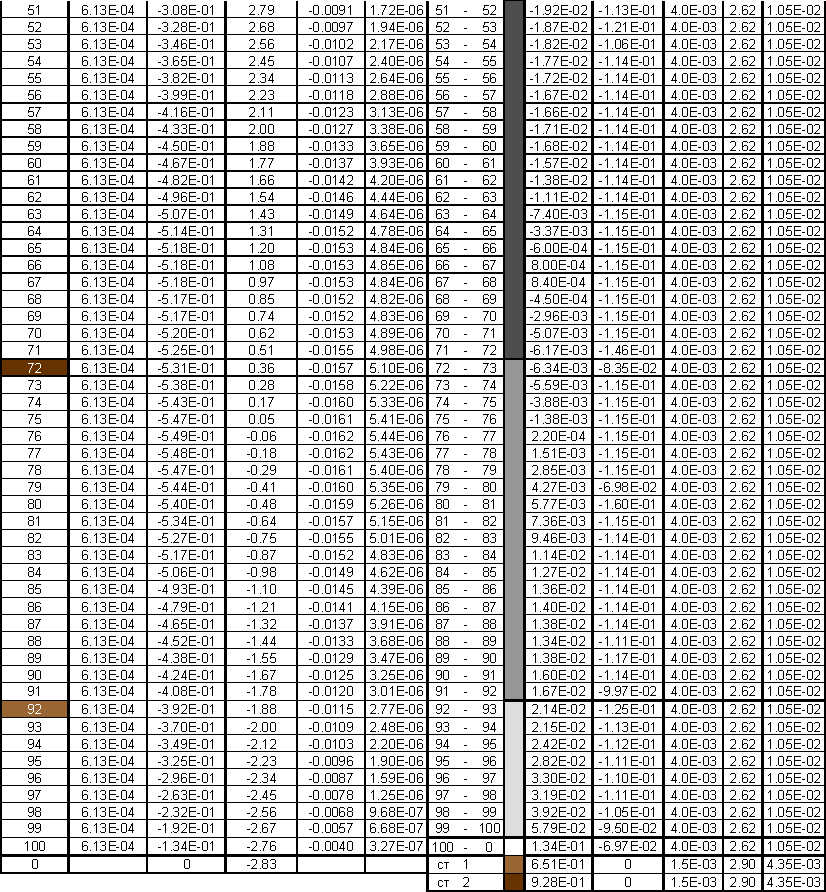
Таблица 9. (Продолжение)

Таблица 9. (Продолжение)

Таблица 9. (Продолжение)
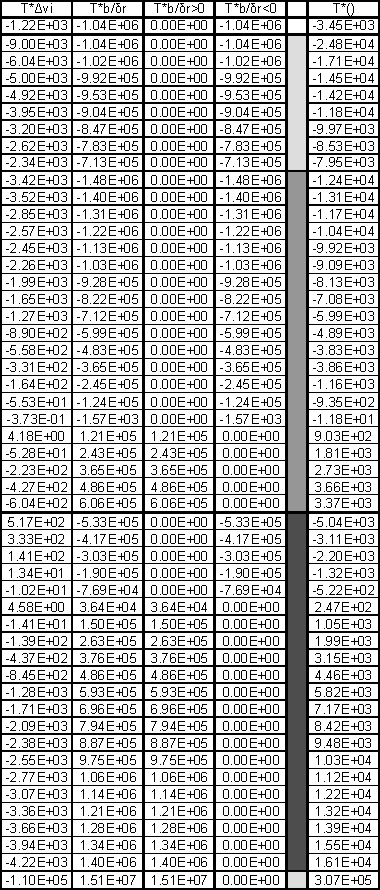
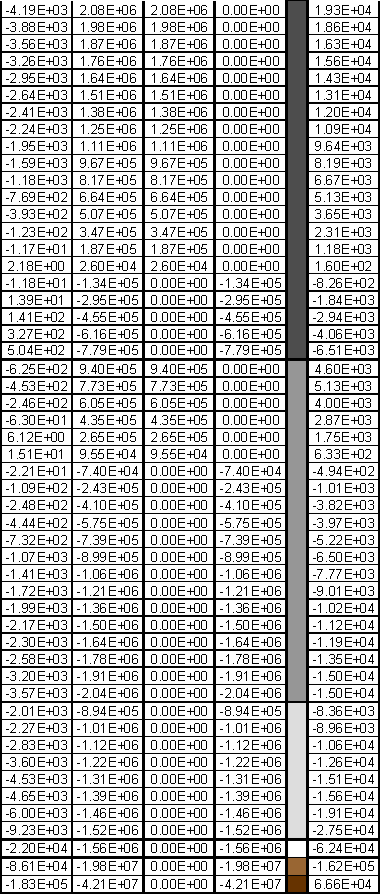
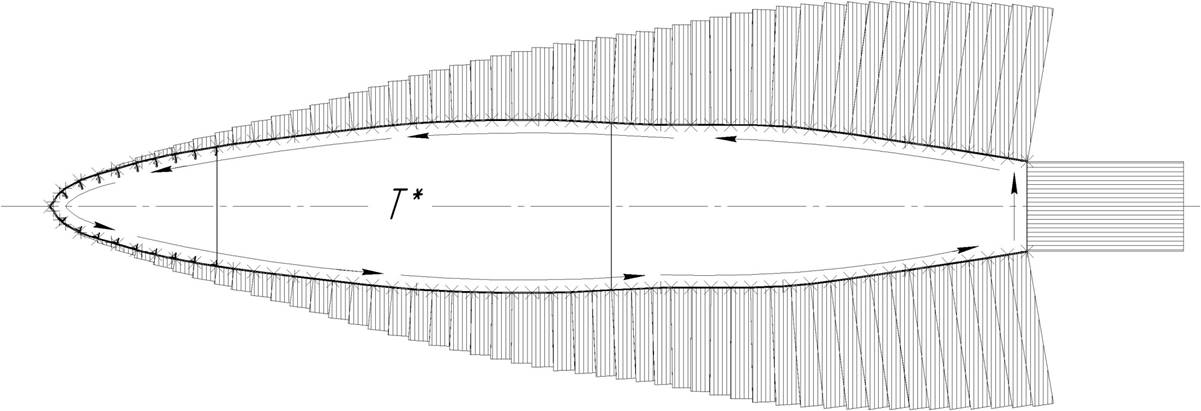
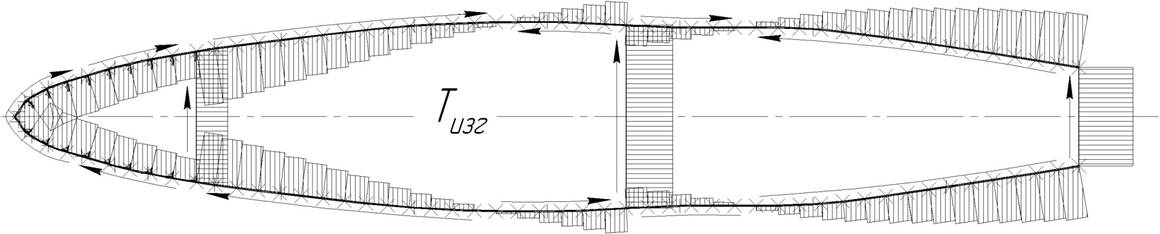
Рис.9 Эпюры касательных сил при простом изгибе
Координату центра жесткости в центральной системе координат u, v можно определить по формуле
![]() .
.
В центральной системе координат координата центра жесткости ![]() .
.
Относительно носка профиля координата центра жесткости ![]() ,
, ![]() .
.
Относительная координата центра жесткости ![]() ,
, ![]() .
.
Крутящий момент относительно оси жесткости крыла возникает
от нормальных к хорде составляющих погонной воздушной нагрузки![]() , от
массовых сил крыла
, от
массовых сил крыла ![]() ,
от массовых сил топлива
,
от массовых сил топлива ![]() и
агрегатов
и
агрегатов ![]() ,
расположенных в крыле.
,
расположенных в крыле.
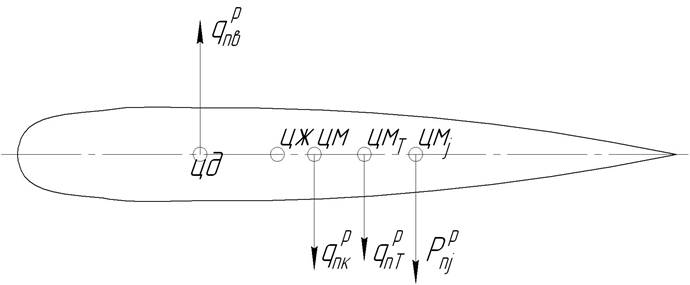
Рис.10 Определение крутящего момента
Погонный крутящий момент в любом сечении определится равенством
![]() , где
, где ![]() - координата
центра жесткости относительно носка профиля;
- координата
центра жесткости относительно носка профиля;
![]() - координата
центра давления относительно носка профиля.
- координата
центра давления относительно носка профиля.
При построении линии центров масс принимаем ![]() .
.
Методом численного интегрирования получим крутящий момент в сечении относительно центра жесткости
![]() , где
, где ![]() - сосредоточенный
момент от агрегата.
- сосредоточенный
момент от агрегата.
Для стреловидного крыла ![]() .
.
Результаты расчета крутящего момента сведены в таблицу 10.
Эпюры погонного и крутящего момента представлены на Рис.11 и Рис.12.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.