Пояснительная записка к курсовой работе по прочности ”Расчет на прочность элементов конструкции самолета”, страница 10

Таблица 6 – Расчет

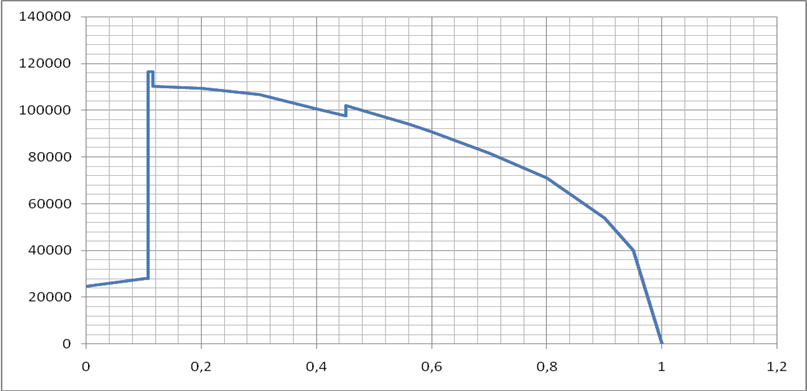
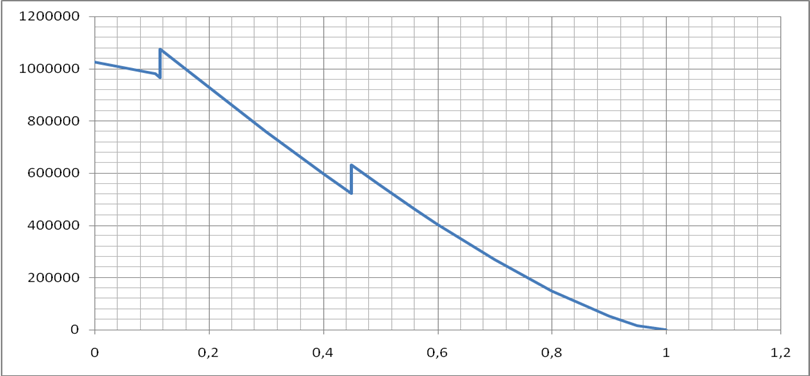
Рисунок 6 – Эпюры погонной нагрузки, перерезывающей силы и изгибающего момента

2.3 Определение нормальных напряжений в сечении прямого крыла методом редукционных коэффициентов

2.3.1 Определение нормальных напряжений в сечениях прямого крыла методом редукционных коэффициентов

Исходными данными для расчета нормальных напряжений в сечении крыла являются размеры и характеристики элементов продольного набора, диаграммы деформаций этих элементов, а также величина изгибающего момента. Схема сечения крыла приведена на рисунке 1.

Величина изгибающего момента в расчетном сечении

Для расчета нормальных напряжений принимаем упрощенные диаграммы деформаций элементов, полагая, что материал всех элементов приведен к дюралю Д16А, а деформирование поясов лонжеронов подчиняется закону Гука при всех нагрузках вплоть до разрушения. Так как пояса лонжеронов в нашем случае выполнены из тех же профилей, что и стрингеры, то редукционный коэффициент для них принимаем равным единице как в растянутой, так и в сжатой зонах .

Диаграмму деформаций дюралевого стрингера в растянутой зоне принимаем до напряжений, равных пределу текучести материала , а в сжатой – до потери устойчивости. Тогда в пределах линейного деформирования стрингера . После появления напряжений, равных пределу текучести или потери устойчивости, диаграмма представляется горизонтальной линией. Напряжения с ростом деформаций не меняются и остаются равными соответственно или . В этом случае редукционный коэффициент для растянутого стрингера будет равен

                                                                       (2.10)

для сжатого

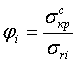                                                           ,                                                                      (2.11)

где - напряжение в стрингере для приведенного сечения.

При определении нормальных напряжений обшивка приводится к продольному набору, и сечение крыла представляется в виде системы дискретных элементов площадью , расположенных в центрах тяжести элементов продольного набора

                                                                                                                        (2.12)

где -истинная площадь сечения i-го элемента продольного набора;

 - приведенная площадь сечения.

Для сжатой и растянутой зон . Тогда для растянутой зоны

Для сжатой зоны

Тогда для растянутой зоны площадь i-го элемента составит

Для сжатой зоны

Для поясов в растянутой и сжатой зоне:

Для поясов в растянутой и сжатой зоне стоящих на задней стенке:

Весь расчет нормальных напряжений проводится последовательными приближениями.

1. Выбираем редукционные коэффициенты в нулевом приближении для дюралевых поясов и стрингеров .
2. Определяем приведенные площади сечений всех элементов для сжатой и растянутой зон, соответственно

3.   Находим положение центра тяжести приведенного сечения в произвольной системе координат (ось проведем параллельно хорде крыла)

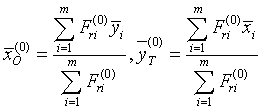,                                                 (2.12)

где m- число элементов продольного набора в сечении;

 - координаты, определяющие положение центра тяжести каждого элемента продольного набора в системе координат .

4. Вычисляем момент инерции приведенного сечения относительно центральных осей

                   (2.13)

где                                                                                     (2.14)

5. Определяем направления главных осей инерции сечения

                                                            (2.15)

6. Находим моменты инерции приведенного сечения относительно главных осей

                             (2.16)

7. Вычисляем изгибающий момент в сечении относительно главной оси

                                                         (2.17)

8. Определяем нормальные напряжения  для всех элементов приведенного сечения в нулевом напряжении

                                                           (2.18)

9. Находим редукционные коэффициенты для сжатых и растянутых стрингеров в первом приближении