Сигнали та їх перетворення. Системи счислення. Коди та їх характеристика. Перешкоди та їх характеристики, страница 21

При виборі функцій  f₀,  f₁, f₂  схемотехніки використовують власний досвід, але при їх удачному виборі апаратна реалізація мінімізованої функції може бути значно економнішою, ніж любі способи прямої реалізації.

Слід зазначити, що інтенсивний розвиток мікросхемотехніки, в тому числі програмуємих логічних матриць (ПЛМ), постійних запам’ятовуючих пристроїв, а також ряду функціональних мікросхем змінили акценти в задачах мінімізації. Широке використання ПЛМ привело до розвитку методів їх програмування. На сучасному рівні їх програмування забезпечується через спеціалізовіані комп’ютерні програми, які одночасно використовують і алгоритмічні засоби мінімізації кількості використовуємих логічних елементів. Одним з таких алгоритмічних методів являється метод Квайна-Мак-Клаксі. Ми не будемо приводити описання таких методів, оскільки вони використовуються і розвиваються розробниками програмних засобів для ПЛМ. Здебільшого - це фірми-виготовлювачі програмуємих логічних матриць, наприклад, ALTERA, XILLINCS  та інші.

           1.7. Коди, що знаходять та коригують помилки.

     1.7.1. Графічна форма представлення логічних функцій.

Ми вже розглянули один з способів графічного представлення логічних функцій – в вигляді карт Карно. Це дало можливість роглядати їх на площині і відкрило ефективний спосіб мінімізації.

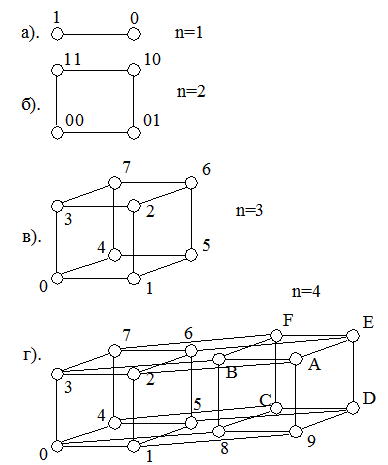В практиці дослідження різних форм представлення логічних функцій широко використовується форма зображення в вигляді n- вимірного куба, де n- довжина строчки двійкового слова. На рис.  приведені геометричні зображення  n-вимірного куба для різних значень  n, що відповідають словам двійкового коду. Кожна вершина відображає одне кодове слово. Така геометрична інтерпретація дає можливість по іншому бачити можливості різних кодів. Наприклад, представлення коду Грея в вигляді 3-вимірного куба має ту особливість, що код кожної сусідньої  вершини відрізняється лише в однму біті.

Важливим моментом такої геометричної інтерпретації являється відстань між двома n- бітними  словами, тобто кількість біт  по яких два слова або дві вершини відрізняються між собою. З точки зору n- куба – це мінімальна довжина шляху, який необхідно пройти ( по ребрах куба) від одної вершини до іншої. Поняття відстані має суттєве значення при розв'язання задач побудови кодів з виявленням помилок в передачі інформації. Структури n-куба широко використовуються і при побудові мультикомп'ютерних і мультипроцесорних обчислювальних систем.

  Будь-який n-куб може розглядатись, подібно до таблиці станів, як поєднання більш простих однотипних структур. Така властивість видима з таблиці станів більшості кодів. Наприклад, двійкові  коди десяткових чисел 0-3 повторюються в кодах чисел 4-7 з різницею в старшому біті коду, що кодує числа в діапазоні 0-7.

Поняття відстані і n-вимірного куба відкривають можливості побудови кодів з виявленням і корекцією помилок при передачі інформації. 

1.7.2. Коди з виявленням і корекцією помилок

Ідеологія побудови таких кодів полягає в тому, що при появі одиночної помилки в кодовому слові, воно вже не відноститься до множини кодових слів даного коду. Така ідеологія легко поясняється на прикладі геометричної інтерпретації коду- n- вимірного куба з використанням поняття відстані, або діапазону.

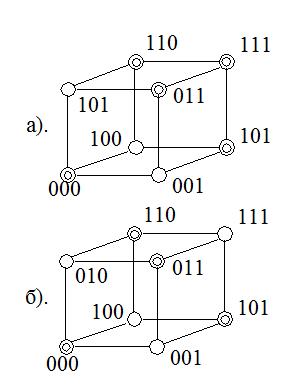На рис.   а приведений приклад коду ( кодові слова позначені більш темними вершинами) в якому зміна в одному біті  ( наприклад, слово 110 замінюється на 111) залишає це слово в наборі кодових слів і тому така помилка при передачі інформації не може бути виявлена. Для коду що представлений в вигляді n-куба, зображеного на рис.   б зміна обного біта будь-якого кодового слова приводить до того, що воно випадає з словаря коду, тому поява помилки в одному біті при передачі коду може бути зразу виявлена.

Виходячи з терміну “мінімальна відстань” між двома кодовими словами n- куба, можна стверджувати, що в конкретному коді можуть біти виявлені всі одиночні помилки, якщо мінімальна відстань між будь-якими парами кодових слів рівняється 2.