Сигнали та їх перетворення. Системи счислення. Коди та їх характеристика. Перешкоди та їх характеристики, страница 18

За своєю застосовуваністю вони різні. Найбільш широке застосування знаходять функції І, АБО, І – НІ, АБО – НІ, ВИКЛ. АБО. Вони універсальні тому, що з їх допомогою можна записати будь-яку іншу функцію.

Розроблений математичний апарат аналізу та синтезу булевих функцій найбільш відпові­дає цим функціям. Набір логічних функцій І, АБО, НІ дозволяє реалізувати будь-яку іншу функцію і називається функціонально повним.

В практичній схемотехниці найбільш поширеними є системи, які реалізують функції І –НІ, АБО-НІ, ВИКЛ. АБО. Вони дозволяють найбільш просто реалізовувати різні функції, мати більшу кількість входів, прості в технічній реалізації.

Теорема Шенона

Широке використання при перетворенні логічних функцій знаходять  теорема Шенона та ряд тотожностей, які витікають з неї.

Теорема Шенона формулюється так: будь-яку функцію n зміних мозна зобразити в формі:

      ( 1.17)

Теорема Шенона являється дуже корисною при виконанні перетворень логічних виразів, що містять операцію ВИКЛ. АБО

Наприклад:

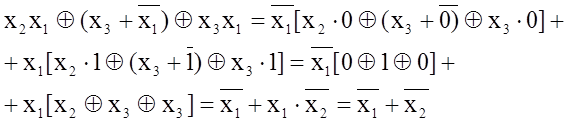
З теоремою Шенона (1.17) пов\язані тотожності:

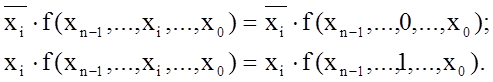            (1.18)

Виходячи з теореми де-Моргана тотожностям (1.18) відповідають слідуючі тотожності:

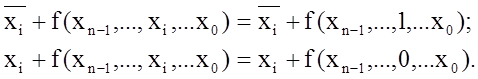               (1.19)

Тотожності (1.18) і (1.19) широко використовуються для спрощення логічних виразів. З них витікають слідуючі широко використовуємі формули:

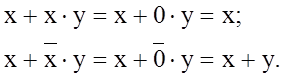
Приведені тотожності дають можливість суттєво спрощувати складні функції багатьох змінних, особливо при наявності заперечень.

Приклад. Спростити слідуючу функцію:

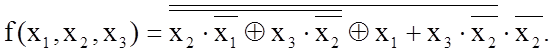
Використовуючи тотожність (1.18) відносно , маємо:

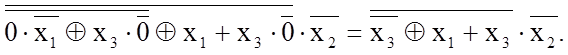
З тотожності (1.19) знаходимо:

В результаті знаходимо:

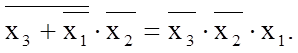
Використання приведених вище тотожностей необхідно для того, щоб розкладати складні логічні функції на більш прості.

Розкладання Ріда

В практиці цифрової схемотехніки широко використовується інший тип розкладання  функцій- розкладання Ріда. Воно базується на використанні слідуючої умови:

Якщо

              то   .

Дійсно,

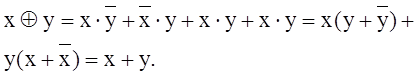
 Це дає можливість розложення Шенона

де

  

зобразити в вигляді:

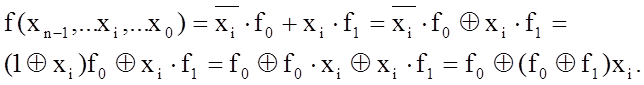
Отриманий вираз і називається розложенням Ріда. Воно дає можливість бідь-яку функцію n змінних зобразити в вигляді полінома n-ї степені виду:

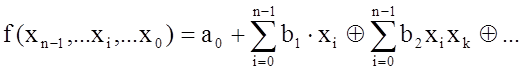
Так, наприклад, функція 2-х змінгних може бути записана в вигляді:

Якщо функція описується поліномами першого ступеня, то вона називається лінійною. Для таких функцій коефіцієнт при логічних добутках змінних =0. В такому випадку для функції 2-х змінних можемо записати:

,

а для функції з кількістю змінних n:

Приклад. Представити функцію

в вигляді лінійного полінома.

Виконуючи перетворення, находимо:

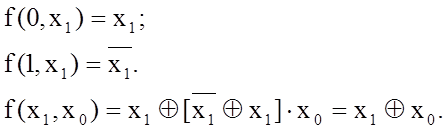
В цифрових пристроях, в яких реалізуються ті чи інші логічні функції, логічні сигнали здебільшого розділяються по функціональному призначенню, наприклад, інформаційні, адресні, керуючі. Вони,відповідно, мають свої умовні познчення. Це дає можливість по вигляду логічних функцій чітко бачити особливості взаємодії між сигналами, взаємозаледність між ними. Деякі приклади таких функцій:

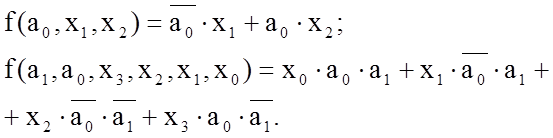
Приведені функції описують роботу простих мультиплексорів. В той же час остання функція може бути представлена в вигляді:

де b₁…b₄ -  коефіцієнти, які являються функціонально залежними від a₀ і a₁.

В якості логічних сигналів можуть використовуватись функції. В такому випадку описуєма логічна функція реалізує функціональний комутатор.

Геметрична інтерпретація логічних функцій.

 Геометричною інтерпретацією логічних функцій являється  використання карт Карно, представлених у ДДНФ (ДКНФ). Карта для двох логічних змінних наведена на рис.1.16. Особливість карти Карно полягає в тому, що по горизонталі та по вертикалі задаються коор­динати клітинок, якими являються аргументи логічної функції. Тому кожна клітина має свою координату – 00, 01, 10, 11, яка  може бути представлена відповідною двійковою або десятковою цифрою. Значення функції записуються в відповідних клітинах нулями та одиницями. Наприклад, функція у₃ зображена двома одиницями і двома нулями в відповідних клітках  карти.